ГДЗ 10-11 Класс Номер 38.17 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

$$y=\{\begin{array}{ll}x,& \text{если }x<0\\ x^{\frac{5}{3}},& \text{если }x\ge 0\end{array}$$

Построить и прочитать график функции:

$$y = \begin{cases} x, & \text{если } x < 0 \\ x^{\frac{5}{3}}, & \text{если } x \geq 0 \end{cases}$$

$y = x$ — уравнение прямой:

$y = x^{\frac{5}{3}}$ — степенная функция:

Графики функций:

Свойства функции:
$D(f) = (-\infty; +\infty)$;
Ни чётная, ни нечётная;
Возрастает на всей числовой прямой;
Не ограничена снизу, не ограничена сверху;
$y_{\min}$ — не существует, $y_{\max}$ — не существует;
Непрерывна на всей области определения;
$E(f) = (-\infty; +\infty)$;
Функция дифференцируема во всех точках, кроме $x = 0$.

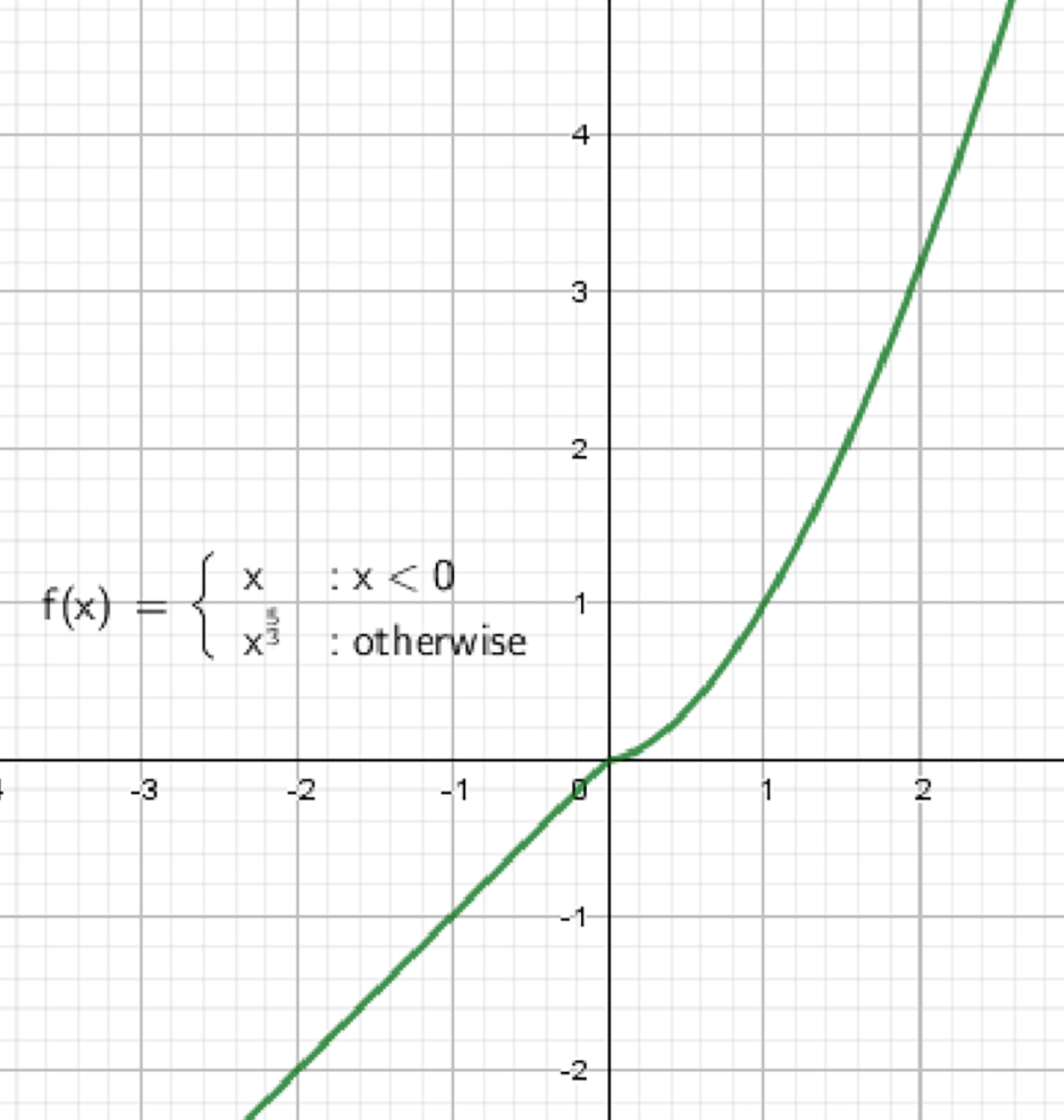
Построить и прочитать график функции

$$y = \begin{cases} x, & \text{если } x < 0 \\ x^{\frac{5}{3}}, & \text{если } x \geq 0 \end{cases}$$

Шаг 1: Анализ вида функции

Это кусочно-заданная функция, то есть она задаётся разными выражениями в разных промежутках:

• При $x < 0$: линейная функция $y = x$
• При $x \geq 0$: степенная функция $y = x^{\frac{5}{3}}$

Шаг 2: Построение графика по частям

1) График функции $y = x$, если $x < 0$

• Это прямая, проходящая через начало координат под углом 45°.
• Мы берём только левую часть от нуля (строго $x < 0$).

Таблица значений:

• Точка $(0; 0)$ не входит (открытая точка), так как знак неравенства — строгий.
• Прямая не продолжается направо от нуля.

2) График функции $y = x^{\frac{5}{3}}$, если $x \geq 0$

• Это степенная функция с дробной положительной степенью:

  $$x^{\frac{5}{3}} = \left( \sqrt[3]{x} \right)^5$$

• Область определения: $x \geq 0$
• Возрастает медленно на малых $x$, быстро на больших.

Таблица значений:

Пояснение по вычислениям:

• $x = 3$:

  $$x^{\frac{5}{3}} = \left( \sqrt[3]{3} \right)^5 \approx 1.442^5 \approx 6.3$$

• $x = 8$:

  $$x^{\frac{5}{3}} = (\sqrt[3]{8})^5 = 2^5 = 32$$

• Точка $(0; 0)$ входит в график (закрашенная), так как $x \geq 0$

Шаг 3: Построение общей функции

• На графике соединяются:
  • Левая часть: прямая до $x = 0$, без точки в нуле (пустой кружок)
  • Правая часть: степенная кривая от $x = 0$ и далее, включая точку (0; 0)

Шаг 4: Проверка непрерывности

• Левая часть стремится к нулю при $x \to 0^{-}$:

  $$\lim_{x \to 0^{-}} x = 0$$

• Правая часть стремится к нулю при $x \to 0^{+}$:

  $$\lim_{x \to 0^{+}} x^{5/3} = 0$$

• Функция не имеет разрыва в точке $x = 0$
  Значения слева и справа сходятся, но производные — разные

Шаг 5: Свойства функции

Область определения

$$D(f) = (-\infty; +\infty)$$

(функция задана при всех $x$)

Чётность

Проверим:

$$f(-x) = \begin{cases} -x, & \text{если } x > 0 \\ (-x)^{5/3}, & \text{если } x \leq 0 \end{cases} \quad \neq f(x)$$

⇒ Функция ни чётная, ни нечётная

Монотонность

• При $x < 0$: функция $f(x) = x$ — возрастает
• При $x \geq 0$: функция $f(x) = x^{5/3}$ — тоже возрастает
• Значит, вся функция возрастает на всей числовой прямой

Ограниченность

• Функция не ограничена сверху: при больших $x$, $y \to +\infty$
• Функция не ограничена снизу: при $x \to -\infty$, $y \to -\infty$

Минимум / максимум

• Наименьшего и наибольшего значения не существует (нет ни нижней, ни верхней границы)

Непрерывность

• Левая и правая части стремятся к одной и той же точке при $x \to 0$
• Значение в точке существует
• Следовательно, функция непрерывна на всей области определения

Область значений

$$E(f) = (-\infty; +\infty)$$

Дифференцируемость

• При $x \ne 0$ — обе части дифференцируемы (гладкие функции)
• В точке $x = 0$ производные слева и справа не совпадают:

  Слева:

  $$f’_-(0) = \lim_{x \to 0^-} 1 = 1$$

  Справа:

  $$f’_+(x) = \frac{5}{3} x^{2/3},\ f’_+(0) = 0$$

• Производная не существует в точке $x = 0$ ⇒ в этой точке функция не дифференцируема

Итог

График:

• Состоит из двух участков:
  • Прямая $y = x$ слева от нуля
  • Кривая $y = x^{5/3}$ справа от нуля
• Соединяются в точке $(0;\ 0)$

Характеристики:

• Область определения: $D(f) = (-\infty;\ +\infty)$
• Область значений: $E(f) = (-\infty;\ +\infty)$
• Непрерывна на всей числовой прямой
• Дифференцируема везде, кроме точки $x = 0$
• Монотонна: возрастает на всей области
• Не чётная, не нечётная
• Не ограничена ни сверху, ни снизу
• Нет $y_{\min}$, нет $y_{\max }$$$\begin{cases} \text{Область определения: } D(f) = (-\infty; +\infty) \\ \text{Функция нечетная и нечетная: нет} \\ \text{Монотонность: возрастает на всей области} \\ \text{Ограниченность: не ограничена ни сверху, ни снизу} \\ \text{Минимум и максимум: не существует} \\ \text{Непрерывность: непрерывна везде} \\ \text{Дифференцируемость: всюду, кроме } x = 0 \\ \text{Область значений: } E(f) = (-\infty; +\infty) \end{cases}$$