ГДЗ 10-11 Класс Номер 38.18 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

$$y=\{\begin{array}{l}\mathrm{\mid }x\mathrm{\mid },\text{ если }x<1\\ x^{\frac{1}{3}},\text{ если }x\ge 1\end{array}$$

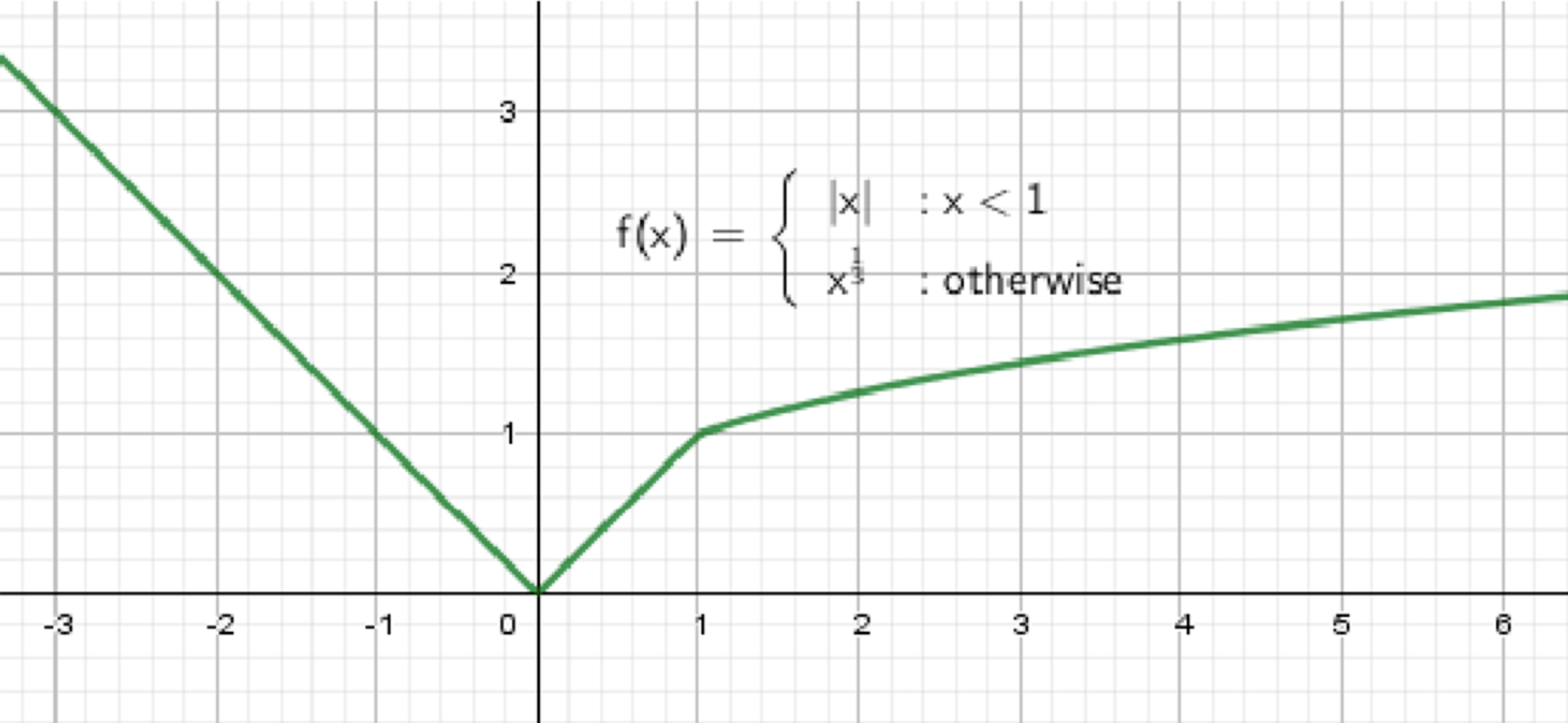
Построить и прочитать график функции:

$$y = \begin{cases} |x|, \text{ если } x < 1 \\ x^{\frac{1}{3}}, \text{ если } x \geq 1 \end{cases}$$

$y = |x|$ — уравнение ломаной:

$y = x^{\frac{1}{3}}$ — степенная функция:

Графики функций:

Свойства функции:

$D(f) = (-\infty; +\infty)$;

Ни чётная, ни нечётная;

Убывает на луче $(-\infty; 0]$ и возрастает на луче $[0; +\infty)$;

Ограничена снизу, не ограничена сверху;

$y_{\text{наим}} = 0$ (в точке $x = 0$);

$y_{\text{наиб}}$ — не существует;

Непрерывна на всей области определения;

$E(f) = [0; +\infty)$;

Функция дифференцируема всюду, кроме точек $x = 0$ и $x = 1$.

Разберём построение и исследование функции:

$$y = \begin{cases} |x|, & \text{если } x < 1 \\ x^{\frac{1}{3}}, & \text{если } x \geq 1 \end{cases}$$

Шаг 1. Анализ общей структуры

Это кусочно-заданная функция.
Она состоит из двух частей:

• Для $x < 1$: $y = |x|$ — модульная функция
• Для $x \geq 1$: $y = x^{\frac{1}{3}}$ — степенная функция с дробной положительной степенью

Мы рассмотрим каждую часть по отдельности, затем соберём в один график и подробно проанализируем свойства.

Шаг 2. Построение графика

Часть 1: $y = |x|$, если $x < 1$

Форма:

• Это ломаная линия, состоящая из двух лучей:
  • $y = -x$, если $x < 0$
  • $y = x$, если $0 \leq x < 1$

Таблица значений:

Комментарии:

• График — буква «V», но мы берём только левую часть до $x = 1$ (включая левый луч, правая половина обрезается на 1)
• Точка $(1; 1)$ — не входит, поскольку неравенство строгое: $x < 1$

Часть 2: $y = x^{\frac{1}{3}}$, если $x \geq 1$

Свойства:

• Это кубический корень, возведённый в 1 степень:

  $$y = \sqrt[3]{x} = x^{1/3}$$

• Определён для всех $x \in \mathbb{R}$, но по условию берём только $x \geq 1$
• Гладкая кривая, возрастающая

Таблица значений:

Комментарии:

• Начинаем график с точки $(1; 1)$, включённой
• График плавно поднимается вверх

Соединение графика

• Левая часть:
  • Ломаная до $x = 1$, точка $(1; 1)$ не включена
• Правая часть:
  • Степенная кривая от $x = 1$, точка $(1; 1)$ включена

Вывод:

• В точке $x = 1$ происходит разрыв по касательной (график «ломается» по наклону)
• Значение слева и справа от 1 совпадает, но производные разные ⇒ не дифференцируема в этой точке

Шаг 3. Исследование свойств функции

1) Область определения (D(f))

• Левая часть определена при $x < 1$
• Правая часть — при $x \geq 1$

⇒

$$D(f) = (-\infty;\ +\infty)$$

2) Чётность / нечётность

Проверим $f(-x)$ и сравним с $f(x)$:

• Например:

  $$f(-2) = |-2| = 2,\quad f(2) = 2^{1/3} \approx 1.26$$

⇒ $f(-x) \ne f(x)$ и $f(-x) \ne -f(x)$

Вывод:
Функция ни чётная, ни нечётная

3) Монотонность

• При $x < 0$: $f(x) = |x| = -x$ — убывает
• При $0 \leq x < 1$: $f(x) = x$ — возрастает
• При $x \geq 1$: $f(x) = x^{1/3}$ — возрастает

Итог:

• Убывает на $(-\infty;\ 0]$
• Возрастает на $[0;\ +\infty)$

4) Ограниченность

• Функция не ограничена сверху:

  $$\lim_{x \to +\infty} x^{1/3} = +\infty$$

• Ограничена снизу:

  $$y_{\min} = 0 \text{ (в точке } x = 0)$$

5) Наименьшее и наибольшее значения

• Наименьшее: $y_{\text{min}} = 0$ при $x = 0$
• Наибольшего нет, поскольку функция убывает слева и возрастает справа до бесконечности

6) Непрерывность

• Обе части непрерывны на своих интервалах
• В точке $x = 1$ проверим:

  $$\lim_{x \to 1^-} |x| = 1,\quad \lim_{x \to 1^+} x^{1/3} = 1$$

• Значение в точке $x = 1$: $f(1) = 1$

Вывод:
Функция непрерывна на всей области определения

7) Дифференцируемость

• Дифференцируема всюду, кроме точек:
  • $x = 0$: излом в модуле (переход от $-x$ к $x$)
  • $x = 1$: переход между двумя функциями, производные не совпадают:

$$f’_-(1) = \frac{d}{dx}|x| = 1,\quad f’_+(1) = \frac{1}{3}x^{-2/3} = \frac{1}{3}$$

Вывод:
Функция не дифференцируема в точках $x = 0$ и $x = 1$

8) Область значений

• Минимум: $y = 0$
• Функция возрастает до $+\infty$

$$E(f)=[0;+\mathrm{\infty })$$