ГДЗ 10-11 Класс Номер 38.19 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

$$y=\{\begin{array}{l}\frac{1}{x},\text{ если }x<0\\ x^{-\frac{1}{2}},\text{ если }x>0\end{array}$$

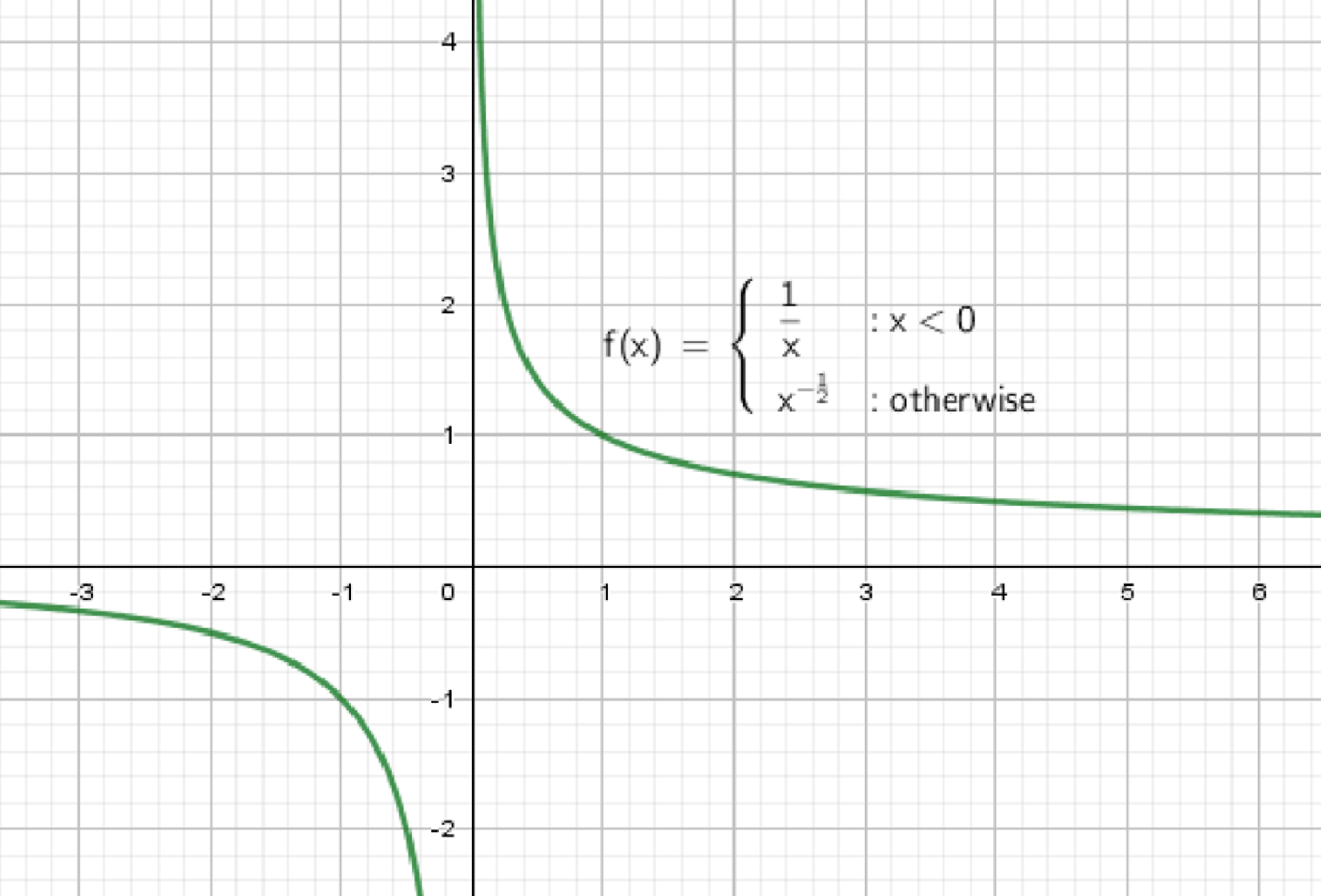
Построить и прочитать график функции:

$$y = \begin{cases} \frac{1}{x}, \text{ если } x < 0 \\ x^{-\frac{1}{2}}, \text{ если } x > 0 \end{cases}$$

1) $y = \frac{1}{x}$ – уравнение гиперболы:

2) $y = x^{-\frac{1}{2}}$ – степенная функция:

3) Графики функций:

4) Свойства функции:

• Область определения:

  $$D(f) = (-\infty; 0) \cup (0; +\infty)$$

• Чётность/нечётность:

  $$f(-x) \neq f(x), \quad f(-x) \neq -f(x)$$

  ⇒ Ни чётная, ни нечётная

• Монотонность:
  Убывает на интервалах:

  $$(-\infty; 0), \quad (0; +\infty)$$

• Асимптоты:
  • Горизонтальная:

    $$\lim_{x \to +\infty} f(x) = \lim_{x \to -\infty} f(x) = 0$$

  • Вертикальная:

    $$\lim_{x \to 0^-} f(x) = -\infty, \quad \lim_{x \to 0^+} f(x) = +\infty$$

    ⇒ $x = 0$ — вертикальная асимптота

• Ограниченность:
  Функция не ограничена ни сверху, ни снизу
• Наибольшее и наименьшее значения:
  Не существуют
• Непрерывность:
  Функция непрерывна на каждом из промежутков:

  $$(-\infty; 0) \quad \text{и} \quad (0; +\infty)$$

  Разрыв в точке $x = 0$

• Область значений:

  $$E(f) = (-\infty; 0) \cup (0; +\infty)$$

• Дифференцируемость:
  Функция дифференцируема всюду, кроме точки $x=0$

Разбираем функцию:

$$y = \begin{cases} \frac{1}{x}, & \text{если } x < 0 \\ x^{-\frac{1}{2}}, & \text{если } x > 0 \end{cases}$$

Шаг 1. Разбор по частям

Часть 1: $y = \dfrac{1}{x}$, если $x < 0$

Это функция гиперболического типа:

• Определена при $x \ne 0$
• При $x < 0$ значение $y < 0$
• При $x \to 0^-$, $y \to -\infty$
• При $x \to -\infty$, $y \to 0^-$

Таблица значений:

Часть 2: $y = x^{-\frac{1}{2}} = \dfrac{1}{\sqrt{x}}$, если $x > 0$

Это степенная функция с отрицательной дробной степенью:

• Определена при $x > 0$
• Значения положительные
• Убывает на всём промежутке $(0; +\infty)$
• При $x \to 0^+$, $y \to +\infty$
• При $x \to +\infty$, $y \to 0^+$

Таблица значений:

Шаг 2. Свойства функции

Область определения

• Левая часть определена при $x < 0$
• Правая часть при $x > 0$

Итог:

$$D(f) = (-\infty; 0) \cup (0; +\infty)$$

Область значений

• Левая часть: $y < 0$
• Правая часть: $y > 0$

Итог:

$$E(f) = (-\infty; 0) \cup (0; +\infty)$$

Асимптоты

• Горизонтальная:

  $$\lim_{x \to \pm\infty} f(x) = 0$$

  ⇒ $y = 0$ — горизонтальная асимптота

• Вертикальная:

  $$\lim_{x \to 0^-} \frac{1}{x} = -\infty,\quad \lim_{x \to 0^+} \frac{1}{\sqrt{x}} = +\infty$$

  ⇒ $x = 0$ — вертикальная асимптота

Непрерывность

• Функция непрерывна на каждом из промежутков:

  $$(-\infty; 0) \quad \text{и} \quad (0; +\infty)$$

• В точке $x = 0$ — разрыв второго рода (левый и правый пределы не совпадают и не конечны)

Дифференцируемость

• Оба выражения дифференцируемы на своих интервалах:
  • $f(x) = \frac{1}{x} \Rightarrow f'(x) = -\frac{1}{x^2}$ при $x < 0$
  • $f(x) = x^{-1/2} \Rightarrow f'(x) = -\frac{1}{2}x^{-3/2}$ при $x > 0$
• В точке $x = 0$ функция не определена, значит не дифференцируема

Монотонность

• $\frac{1}{x}$ убывает при $x < 0$
• $\frac{1}{\sqrt{x}}$ убывает при $x > 0$

Итог:
Функция убывает на обоих промежутках

Чётность / нечётность

Проверим:

$$f(-x) \neq f(x),\quad f(-x) \neq -f(x)$$

Функция не является ни чётной, ни нечётной

Ограниченность

• Снизу не ограничена, так как $\lim_{x \to 0^-} f(x) = -\infty$
• Сверху не ограничена, так как $\lim_{x \to 0^+} f(x) = +\infty$

Экстремумы

• На каждом из промежутков функция строго убывает
• Ни минимума, ни максимума не достигается

Итог