ГДЗ 10-11 Класс Номер 38.2 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y = x^{\frac{3}{2}}$;

б) $y = x^{\frac{1}{4}}$;

в) $y = x^{-\frac{1}{2}}$;

г) $y = x^{\frac{5}{4}}$

Построить график функции:

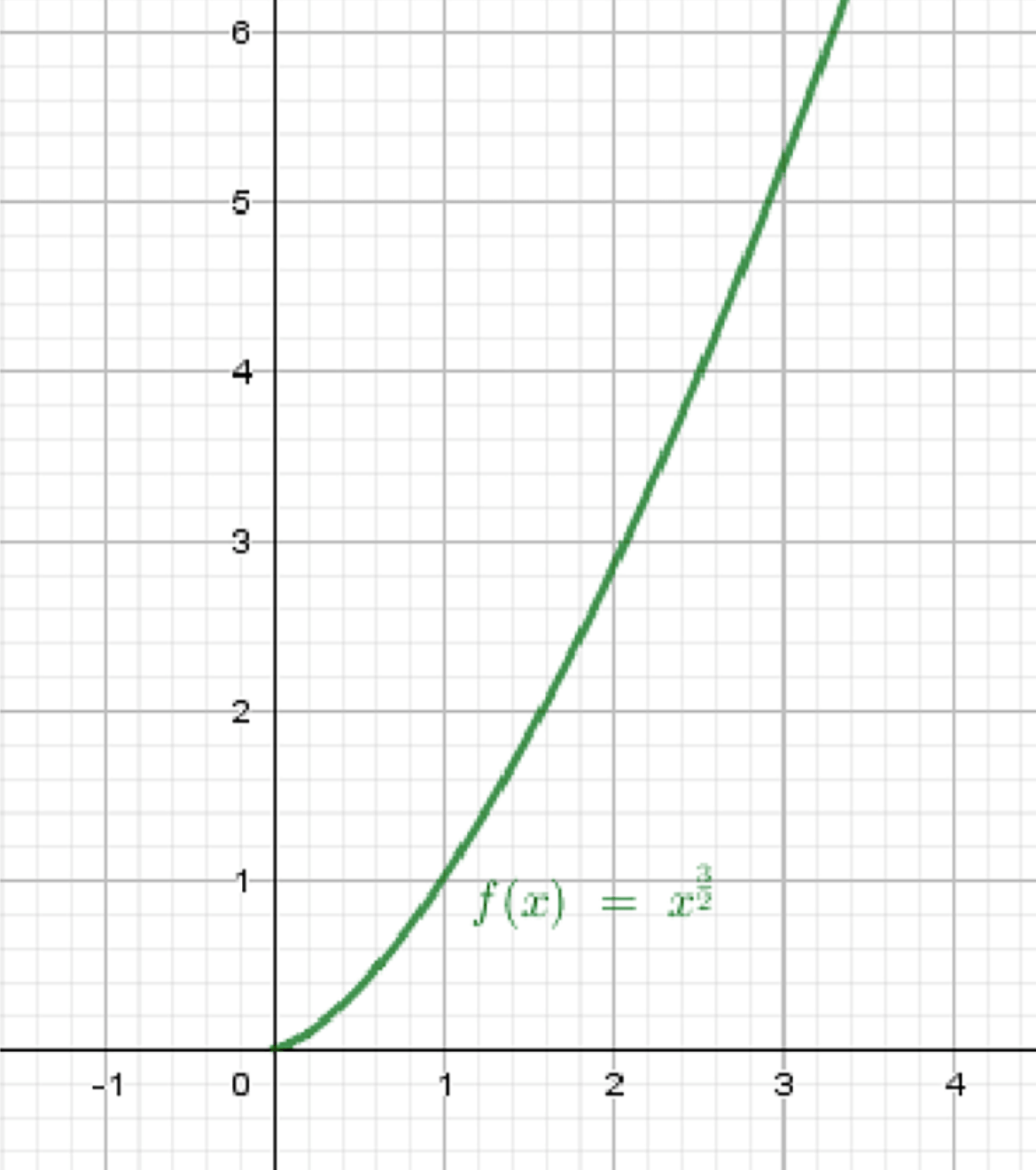
а) $y = x^{\frac{3}{2}}$;
Функция возрастает и выпукла вниз:

График функции:

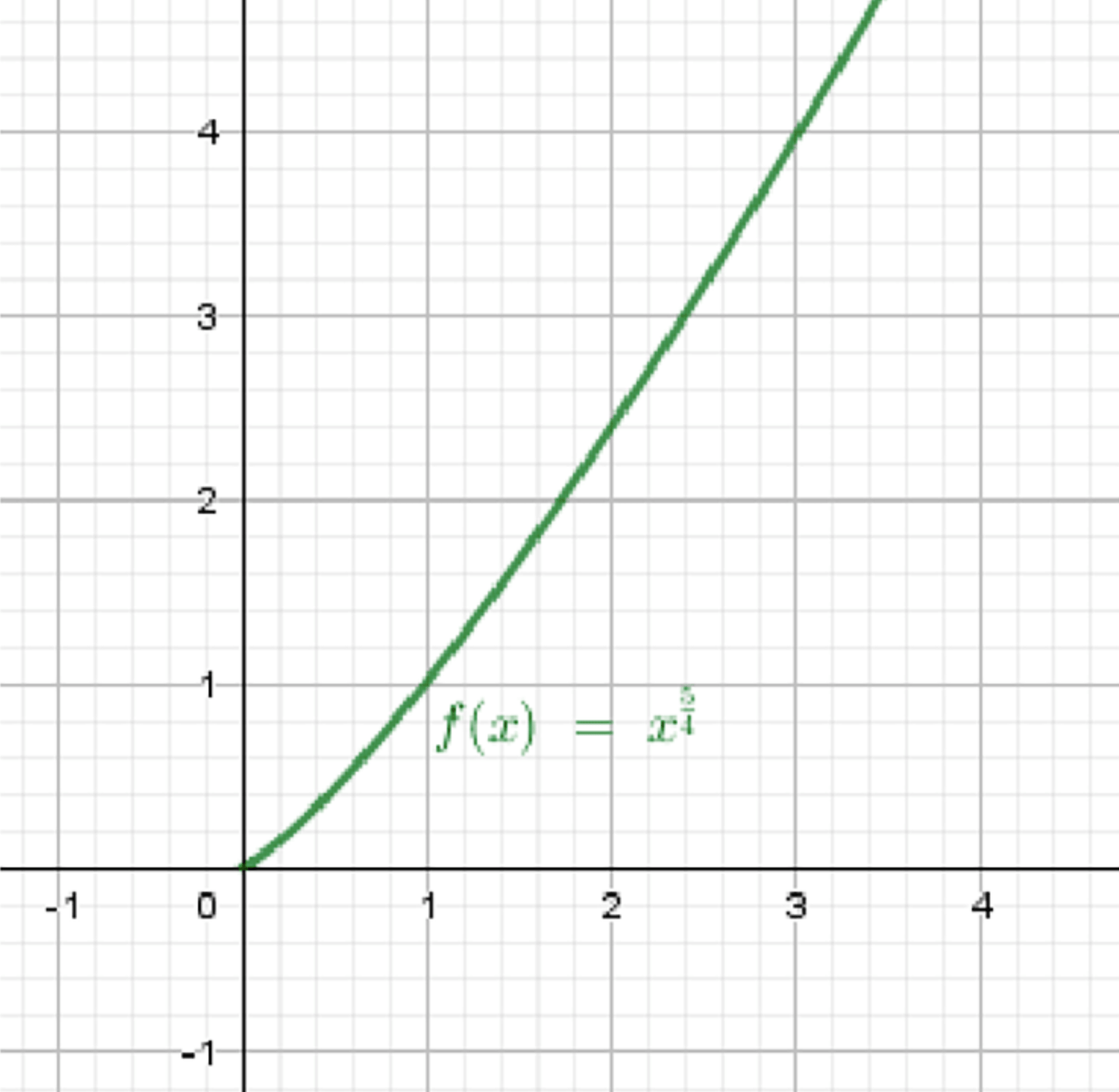
б) $y = x^{\frac{1}{4}}$;
Функция возрастает и выпукла вверх:

График функции:

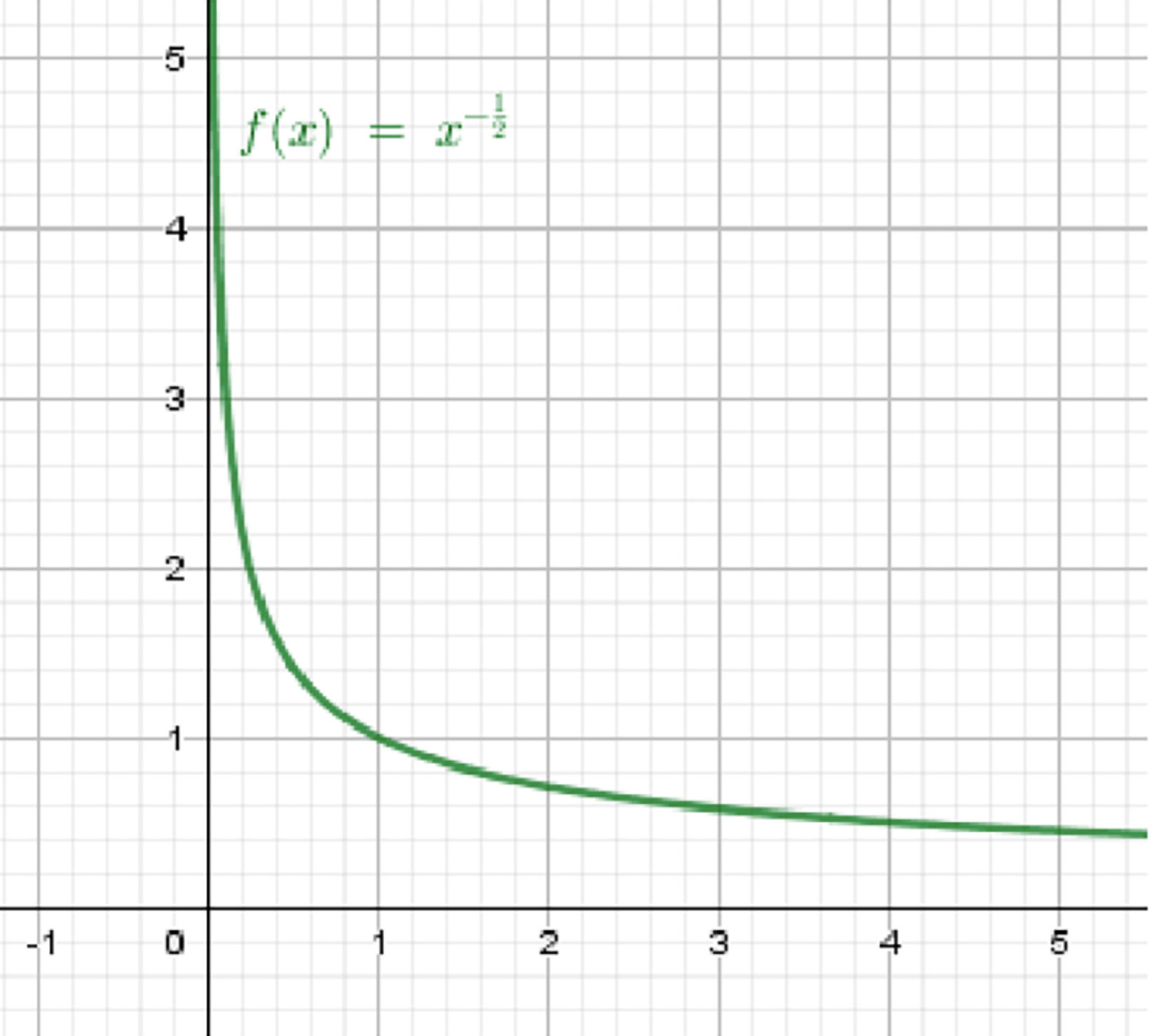
в) $y = x^{-\frac{1}{2}}$;
Функция убывает и выпукла вниз:

График функции:

г) $y = x^{\frac{5}{4}}$;
Функция возрастает и выпукла вниз:

График функции:

а) $y = x^{\frac{3}{2}}$

1. Область определения

Степень $\frac{3}{2}$ — положительное рациональное число.
Представим степень в виде корня:

$$x^{\frac{3}{2}} = \left( \sqrt{x} \right)^3$$

Корень чётной степени определён только для неотрицательных значений $x$.

Вывод:

$$D(y) = [0; +\infty)$$

2. Поведение функции

• Поскольку степень больше 1, функция возрастает.
• Вторая производная $y» > 0$ для $0 < x < 1$, затем $y» < 0$, значит:
  Функция выпукла вниз на $(0; +\infty)$.

3. Таблица значений

$$\begin{align*} x = 0 &\Rightarrow y = 0^{\frac{3}{2}} = 0 \\ x = 1 &\Rightarrow y = 1^{\frac{3}{2}} = 1 \\ x = 4 &\Rightarrow y = 4^{\frac{3}{2}} = (\sqrt{4})^3 = 2^3 = 8 \\ \end{align*}$$

Таблица:

4. Характер графика

• Проходит через точки: (0;0), (1;1), (4;8)
• Монотонно возрастает
• Выпуклая вниз (кривая «отогнута вниз»)

б) $y = x^{\frac{1}{4}}$

1. Область определения

Представим степень в виде корня:

$$x^{\frac{1}{4}} = \sqrt[4]{x}$$

Корень четвёртой степени определён только для $x \geq 0$.

Вывод:

$$D(y) = [0; +\infty)$$

2. Поведение функции

• Степень $\frac{1}{4} < 1$, функция возрастает медленно
• Вторая производная $y» > 0$, то есть функция выпуклая вверх

3. Таблица значений

$$\begin{align*} x = 0 &\Rightarrow y = 0^{\frac{1}{4}} = 0 \\ x = 1 &\Rightarrow y = 1^{\frac{1}{4}} = 1 \\ x = 16 &\Rightarrow y = 16^{\frac{1}{4}} = \sqrt[4]{16} = \sqrt{\sqrt{16}} = \sqrt{4} = 2 \\ \end{align*}$$

Таблица:

4. Характер графика

• Проходит через точки: (0;0), (1;1), (16;2)
• Монотонно возрастает
• Выпуклая вверх (кривая «вогнута вверх»)

в) $y = x^{-\frac{1}{2}}$

1. Область определения

Отрицательная степень с чётным корнем:

$$x^{-\frac{1}{2}} = \frac{1}{\sqrt{x}}$$

Корень определён только для $x > 0$, и делить на 0 нельзя.

Вывод:

$$D(y) = (0; +\infty)$$

2. Поведение функции

• Степень отрицательная ⇒ функция убывает
• Производные показывают, что вторая производная $y» < 0$ ⇒ выпуклая вниз

3. Таблица значений

$$\begin{align*} x = 0.25 &\Rightarrow y = (0.25)^{-\frac{1}{2}} = \frac{1}{\sqrt{0.25}} = \frac{1}{0.5} = 2 \\ x = 1 &\Rightarrow y = 1^{-\frac{1}{2}} = \frac{1}{\sqrt{1}} = 1 \\ x = 4 &\Rightarrow y = 4^{-\frac{1}{2}} = \frac{1}{\sqrt{4}} = \frac{1}{2} = 0.5 \\ \end{align*}$$

Таблица:

4. Характер графика

• Проходит через точки: (0.25;2), (1;1), (4;0.5)
• Монотонно убывает
• Выпуклая вниз (кривая «отогнута вниз»)

г) $y = x^{\frac{5}{4}}$

1. Область определения

$$x^{\frac{5}{4}} = \left( \sqrt[4]{x} \right)^5$$

Корень четвёртой степени требует $x \geq 0$.

Вывод:

$$D(y) = [0; +\infty)$$

2. Поведение функции

• Степень $\frac{5}{4} > 1$, значит функция возрастает
• Поскольку степень больше 1, и вторая производная меняет знак, функция выпуклая вниз

3. Таблица значений

$$\begin{align*} x = 0 &\Rightarrow y = 0^{\frac{5}{4}} = 0 \\ x = 1 &\Rightarrow y = 1^{\frac{5}{4}} = 1 \\ x = 5 &\Rightarrow y = 5^{\frac{5}{4}} \approx 7.5 \\ \end{align*}$$

Таблица:

4. Характер графика

• Проходит через точки: (0;0), (1;1), (5;≈7.5)
• Монотонно возрастает
• Выпуклая вниз