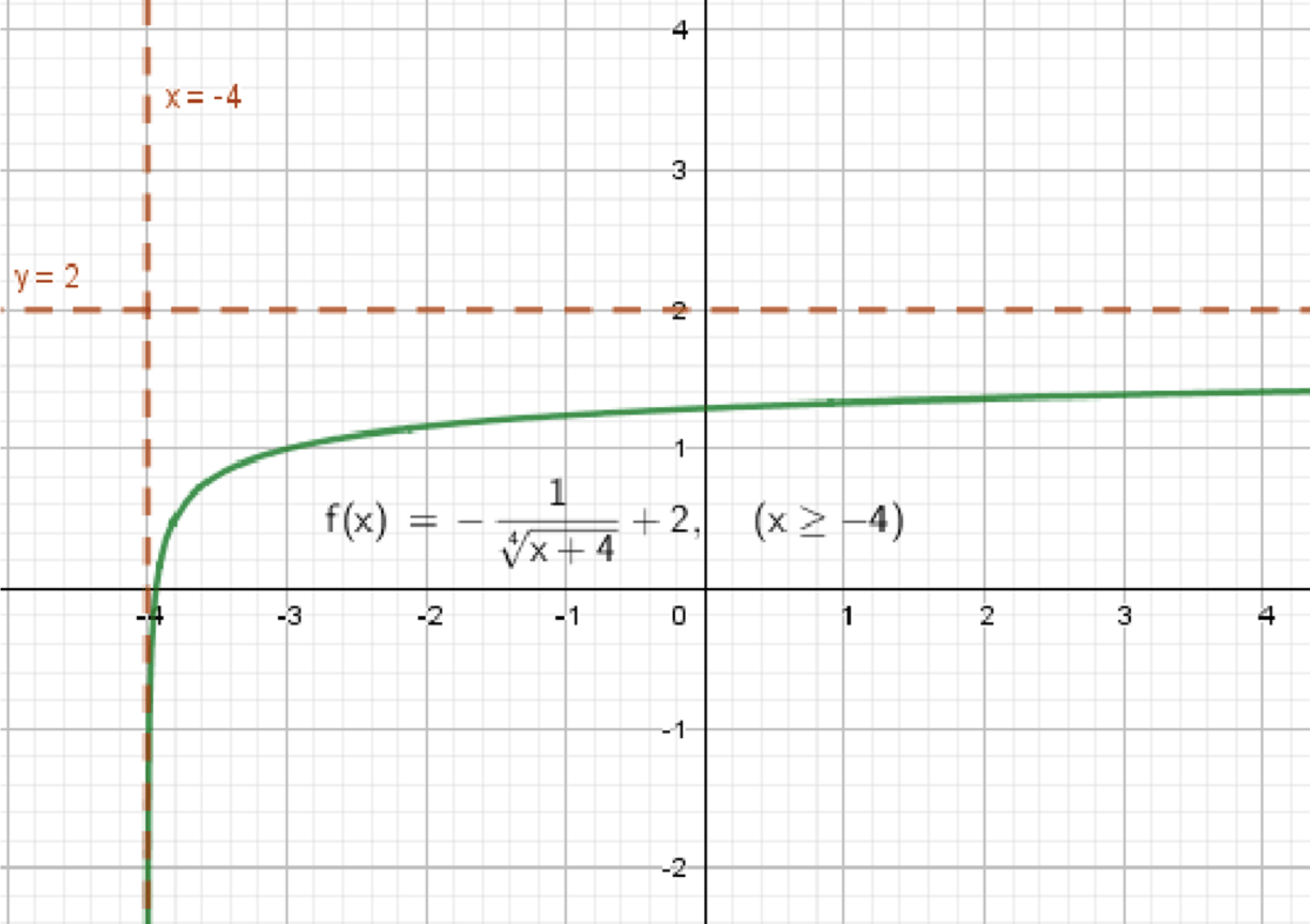ГДЗ 10-11 Класс Номер 38.33 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = 2(x — 1)^{\frac{2}{3}} — 2$;

б) $y = -\frac{1}{\sqrt[4]{x + 4}} + 2 = -(x + 4)^{-\frac{1}{4}} + 2$;

в) $y = -(x + 2)^{\frac{3}{2}} + 1$;

г) $y = 1{,}5(x — 3)^{-\frac{2}{7}} — 4$

Построить график функции:

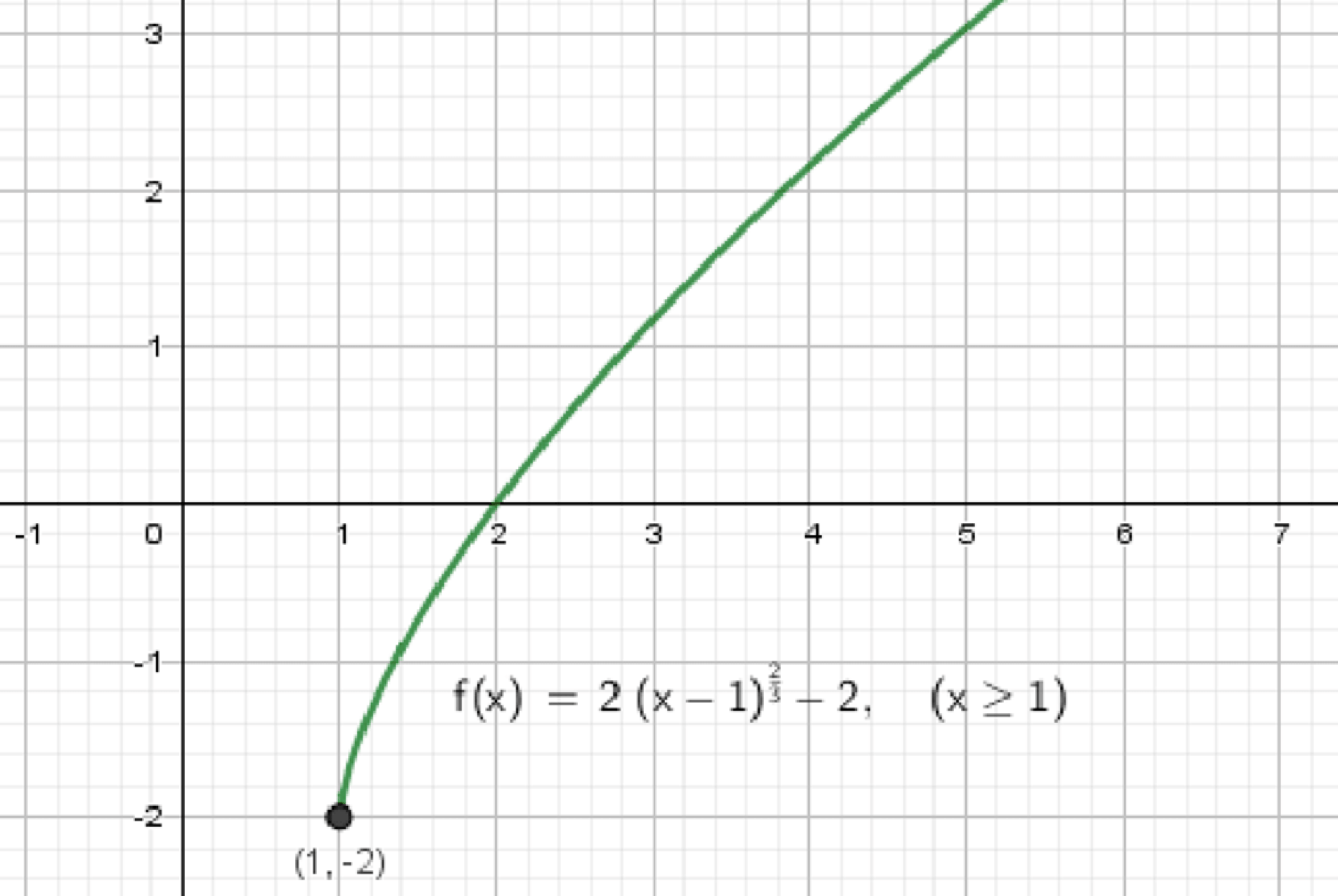
а) $y = 2(x — 1)^{\frac{2}{3}} — 2$;
Построим график функции $y = x^{\frac{2}{3}}$;
Переместим его на 1 единицу вправо;
Растянем его в 2 раза от оси абсцисс;
Переместим его на 2 единицы вниз:

б) $y = -\frac{1}{\sqrt[4]{x + 4}} + 2 = -(x + 4)^{-\frac{1}{4}} + 2$;
Построим график функции $y = x^{-\frac{1}{4}}$;
Переместим его на 4 единицы влево;
Отразим его относительно оси абсцисс;
Переместим его на 2 единицы вверх:

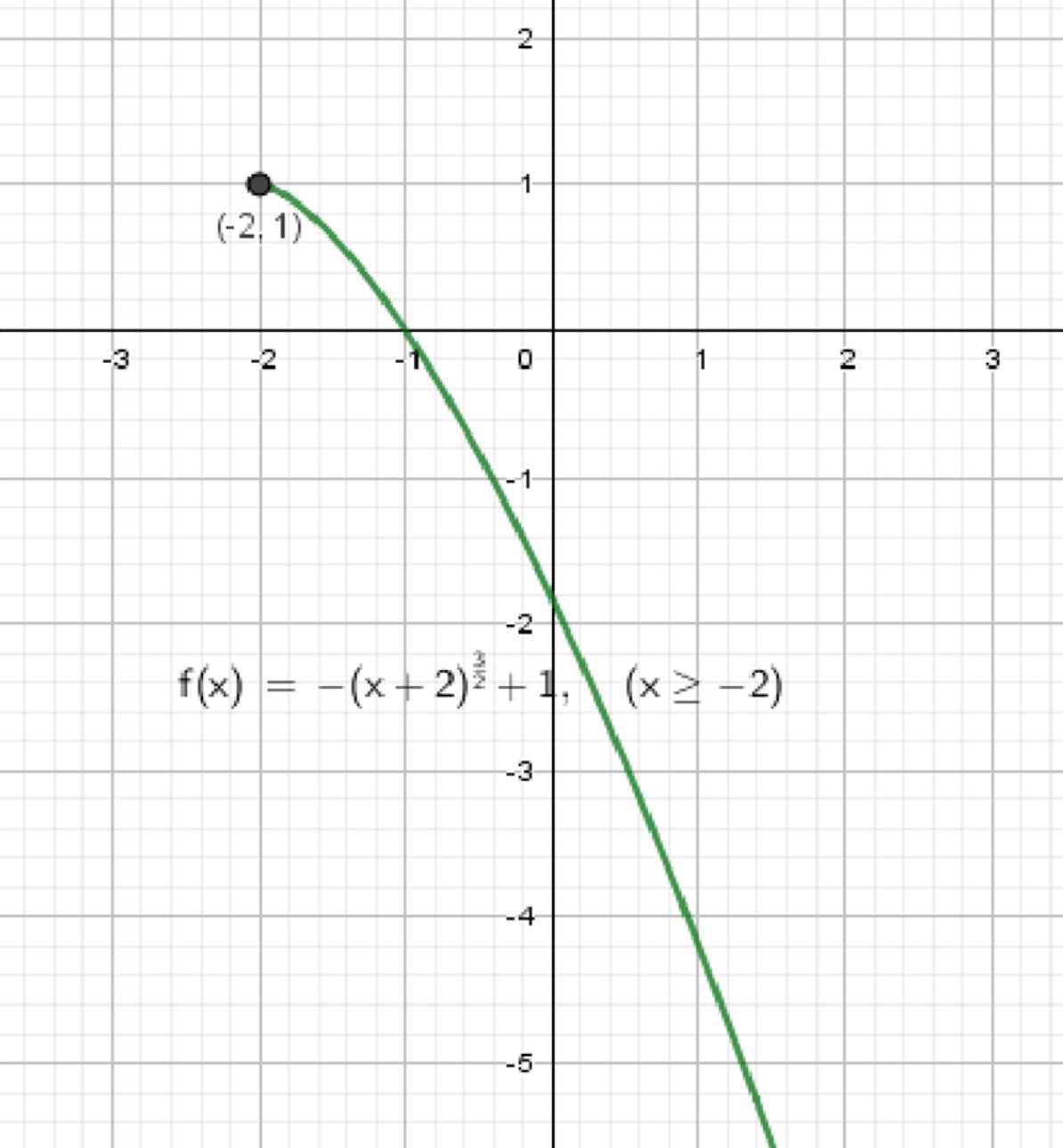
в) $y = -(x + 2)^{\frac{3}{2}} + 1$;
Построим график функции $y = x^{\frac{3}{2}}$;
Переместим его на 2 единицы влево;
Отразим его относительно оси абсцисс;
Переместим его на 1 единицу вверх:

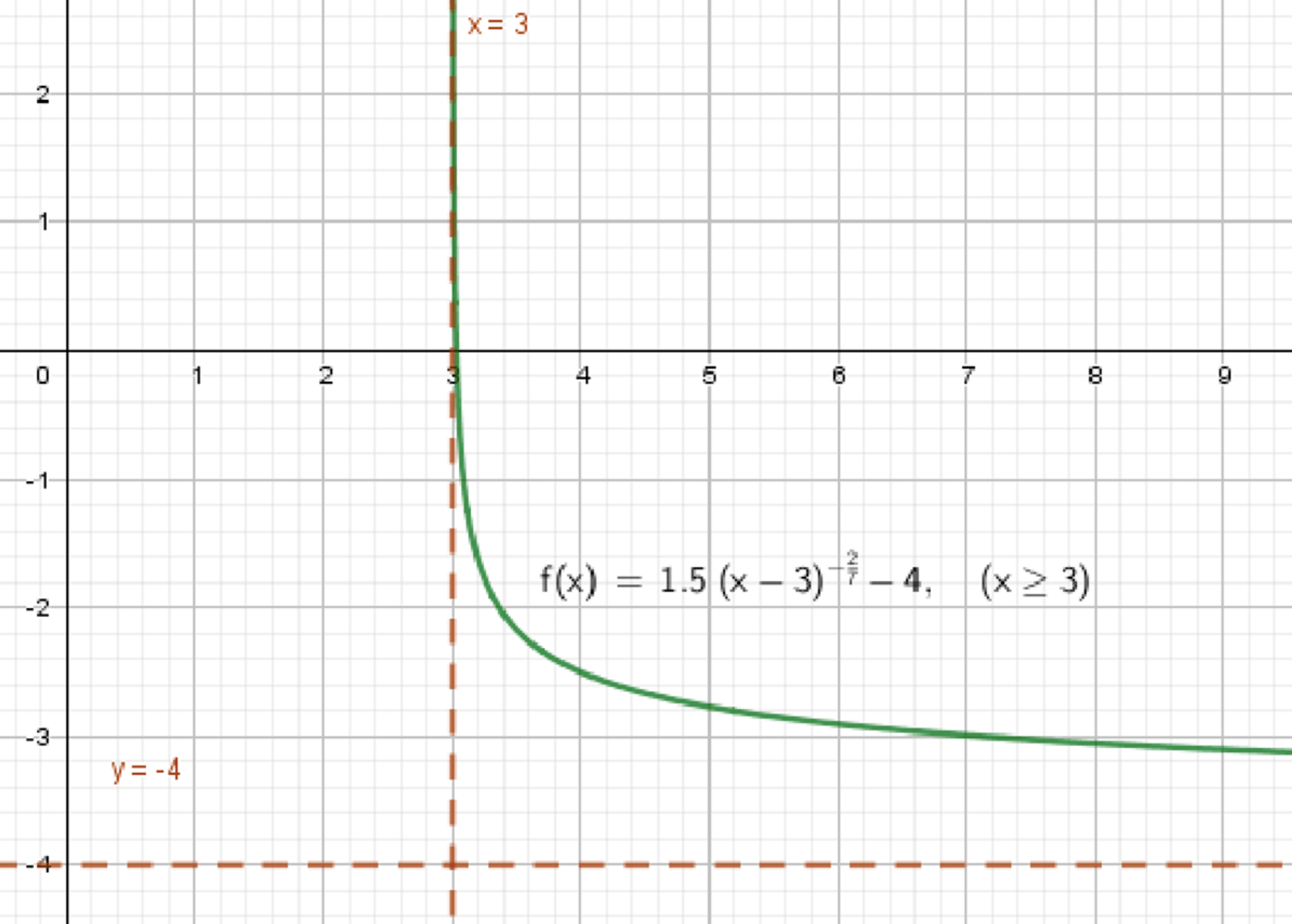
г) $y = 1{,}5(x — 3)^{-\frac{2}{7}} — 4$;
Построим график функции $y = x^{-\frac{2}{7}}$;
Переместим его на 3 единицы вправо;
Растянем его в 1,5 раза от оси абсцисс;
Переместим его на 4 единицы вниз:

а)

$$y = 2(x — 1)^{\frac{2}{3}} — 2$$

Шаг 1: Базовая функция

Рассмотрим базовую функцию:

$$f(x) = x^{\frac{2}{3}}$$

Свойства:

• Определена при всех $x \in \mathbb{R}$
• Чётная: $f(-x) = f(x)$
• Значения всегда неотрицательны: $f(x) \geq 0$
• Имеет минимум в точке $x = 0$, где $f(0) = 0$
• Поведение около нуля: «угловая точка» (функция непрерывна, но производная стремится к бесконечности)

Шаг 2: Горизонтальный сдвиг

Подставим:

$$x \rightarrow x — 1 \Rightarrow f(x) = (x — 1)^{\frac{2}{3}}$$

Изменения:

• График сдвигается вправо на 1 единицу
• Новая вершина (минимум) — точка $x = 1$

Шаг 3: Вертикальное растяжение

Умножаем на 2:

$$f(x) = 2(x — 1)^{\frac{2}{3}}$$

Изменения:

• График растянут по вертикали в 2 раза
• Все значения $y$ становятся в 2 раза больше по модулю

Шаг 4: Вертикальный сдвиг вниз

Вычитаем 2:

$$f(x) = 2(x — 1)^{\frac{2}{3}} — 2$$

Изменения:

• График опущен вниз на 2 единицы
• Минимум теперь находится в точке $x = 1$, $y = -2$

Итоговое описание графика (а):

• Определён на всей числовой прямой
• Минимум в точке $(1; -2)$
• График симметричен относительно прямой $x = 1$
• Ветви стремятся вверх по мере удаления от точки 1
• Форма «загнута» вверх, напоминает округлую V-образную форму с гладким изгибом

б)

$$y = -\frac{1}{\sqrt[4]{x + 4}} + 2 = -(x + 4)^{-\frac{1}{4}} + 2$$

Шаг 1: Базовая функция

Рассмотрим $f(x) = x^{-\frac{1}{4}}$

Свойства:

• Определена при $x > 0$
• Убывает: по мере увеличения $x$, значение функции уменьшается
• При $x \to 0^+$, $f(x) \to +\infty$
• При $x \to +\infty$, $f(x) \to 0$

Шаг 2: Горизонтальный сдвиг

Подставим $x \rightarrow x + 4$:

$$f(x) = (x + 4)^{-\frac{1}{4}}$$

Изменения:

• График сдвинут влево на 4 единицы
• Область определения: $x > -4$

Шаг 3: Отражение относительно оси абсцисс

Меняем знак:

$$f(x) = -(x + 4)^{-\frac{1}{4}}$$

Изменения:

• Все значения $y$ меняются на противоположные
• Теперь:
  • При $x \to -4^+$, $y \to -\infty$
  • При $x \to +\infty$, $y \to 0^-$

Шаг 4: Вертикальный сдвиг вверх

Добавим 2:

$$y = -(x + 4)^{-\frac{1}{4}} + 2$$

Изменения:

• График поднят вверх на 2 единицы
• Асимптота: горизонтальная прямая $y = 2$ (снизу)

Итоговое описание графика (б):

• Область определения: $x > -4$
• Стремится к $-\infty$ при $x \to -4^+$
• Стремится к 2 (снизу) при $x \to +\infty$
• График расположен ниже оси абсцисс, затем поднимается и асимптотически приближается к 2
• Плавно убывает слева направо, с резким спадом около $x = -4$

в)

$$y = -(x + 2)^{\frac{3}{2}} + 1$$

Шаг 1: Базовая функция

Рассмотрим $f(x) = x^{\frac{3}{2}}$

Свойства:

• Определена при $x \geq 0$
• Возрастает
• Убыстряющий рост: $f(x) \sim x \sqrt{x}$
• Начинается из точки $(0; 0)$

Шаг 2: Горизонтальный сдвиг

Подставим $x \rightarrow x + 2$:

$$f(x) = (x + 2)^{\frac{3}{2}}$$

Изменения:

• График сдвинут влево на 2 единицы
• Новое начало — точка $x = -2$

Шаг 3: Отражение относительно оси абсцисс

Меняем знак:

$$f(x) = -(x + 2)^{\frac{3}{2}}$$

Изменения:

• Все значения $y$ становятся отрицательными
• Функция теперь убывает

Шаг 4: Вертикальный сдвиг вверх

Добавим 1:

$$y = -(x + 2)^{\frac{3}{2}} + 1$$

Изменения:

• График поднят вверх на 1 единицу
• Точка $(-2; 1)$ — максимум

Итоговое описание графика (в):

• Область определения: $x \geq -2$
• Вершина (максимум) в точке $(-2; 1)$
• График убывает на всём своём промежутке
• Плавная кривая, спадающая вниз
• Поведение: крутое падение сначала, затем замедляется

г)

$$y = 1{,}5(x — 3)^{-\frac{2}{7}} — 4$$

Шаг 1: Базовая функция

Рассмотрим $f(x) = x^{-\frac{2}{7}}$

Свойства:

• Определена при $x > 0$
• Всегда положительна
• Стремится к $+\infty$ при $x \to 0^+$
• Стремится к 0 при $x \to +\infty$

Шаг 2: Горизонтальный сдвиг

Подставим $x \rightarrow x — 3$:

$$f(x) = (x — 3)^{-\frac{2}{7}}$$

Изменения:

• График сдвигается вправо на 3 единицы
• Новая область определения: $x > 3$

Шаг 3: Вертикальное растяжение

Умножаем на 1,5:

$$f(x) = 1{,}5(x — 3)^{-\frac{2}{7}}$$

Изменения:

• График растянут вверх в 1{,}5 раза
• Значения становятся больше по модулю

Шаг 4: Вертикальный сдвиг вниз

Вычитаем 4:

$$y = 1{,}5(x — 3)^{-\frac{2}{7}} — 4$$

Изменения:

• График опущен вниз на 4 единицы
• Асимптота: горизонтальная прямая $y = -4$

Итоговое описание графика (г):

• Область определения: $x > 3$
• При $x \to 3^+$, $y \to +\infty$
• При $x \to +\infty$, $y \to -4$ (сверху)
• График расположен выше прямой $y = -4$, но стремится к ней сверху
• Плавно убывает, асимптотически приближаясь к $y=-4$