Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 38.34 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите графически неравенство:
а) ;
б) ;
в) ;
г)
Решить графически неравенство:
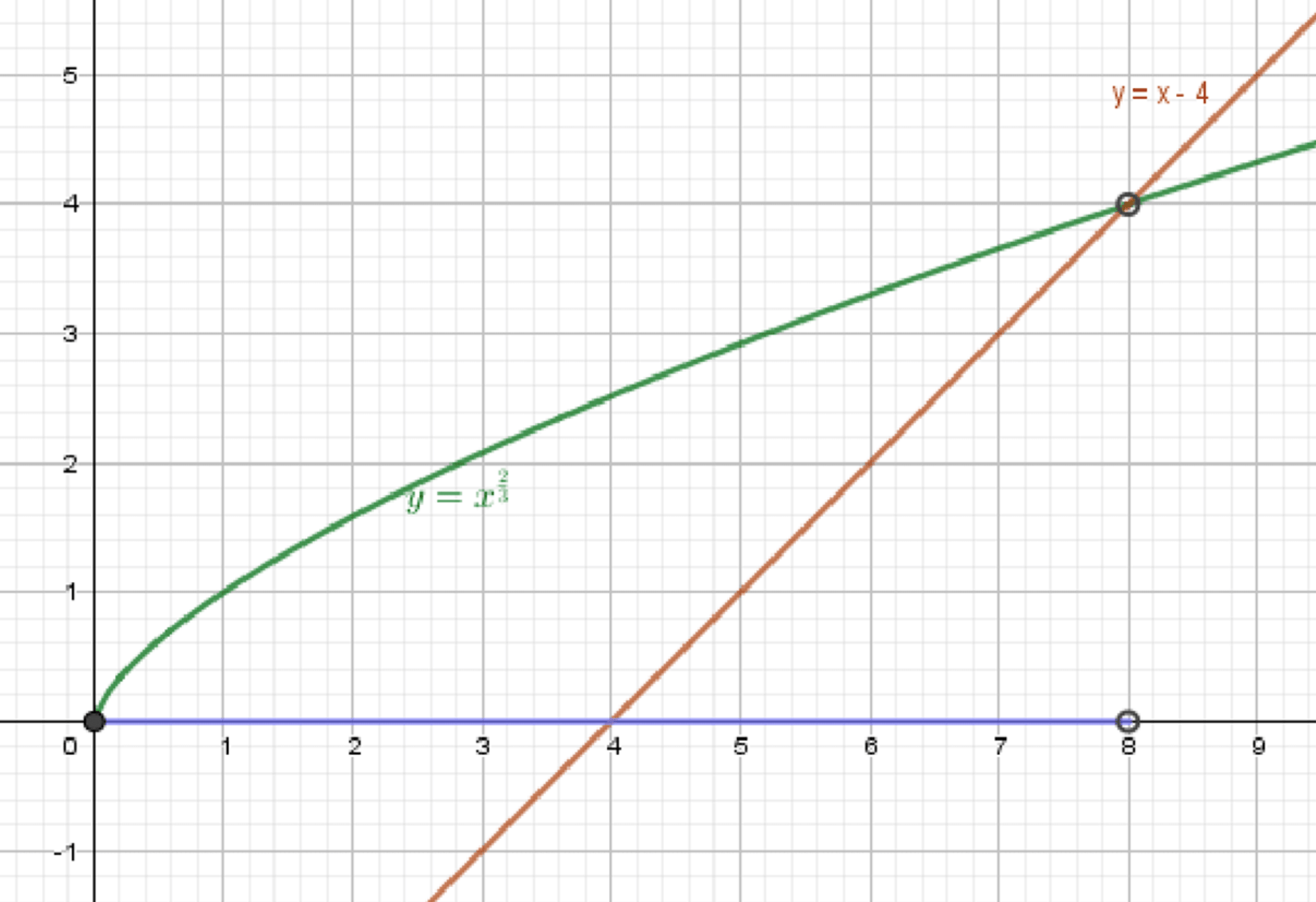
а) ;
– степенная функция:
– уравнение прямой:
Графики функций:
Ответ: .
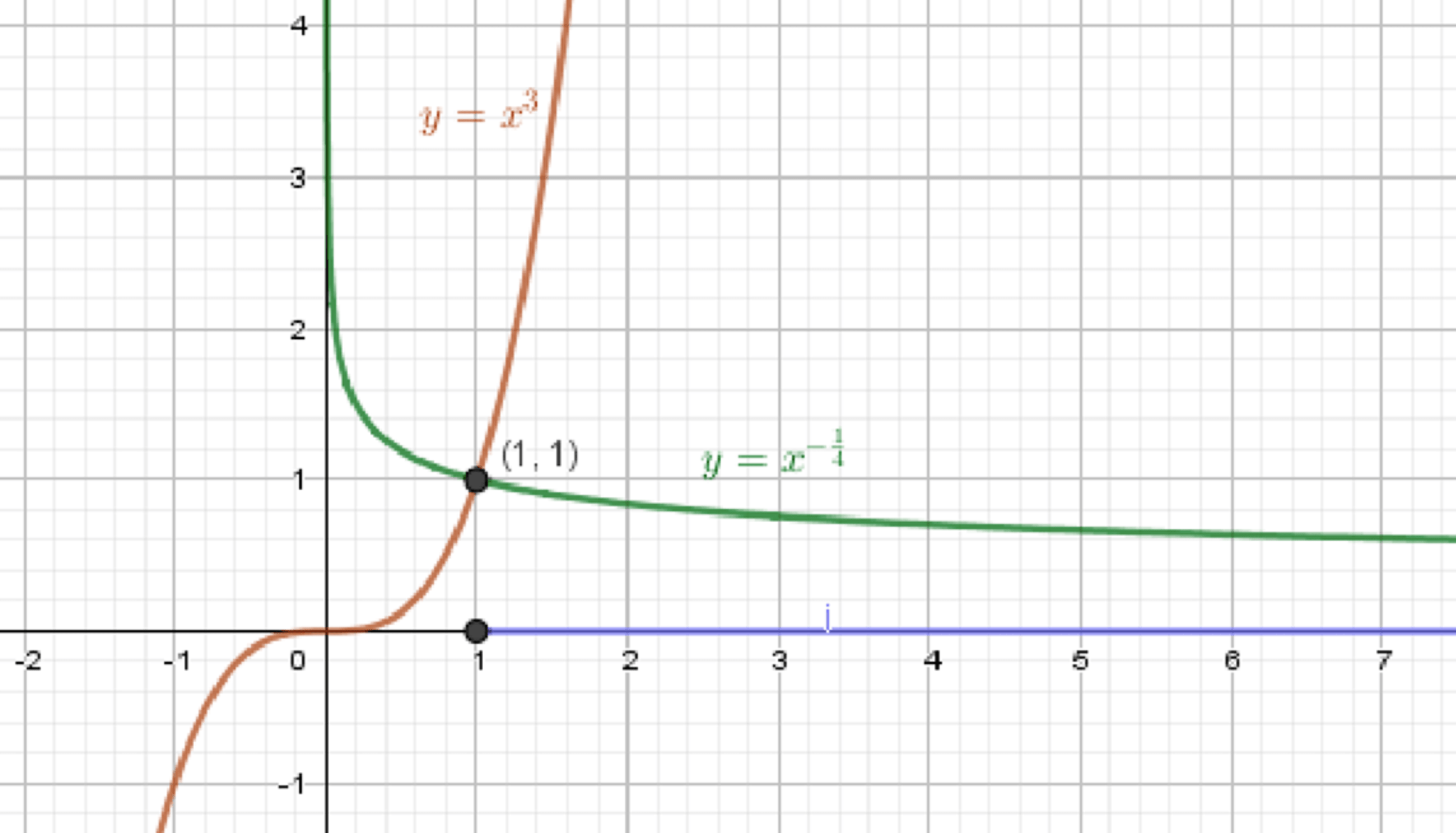
б) ;
– степенная функция:
– степенная функция:
Графики функций:
Ответ: .
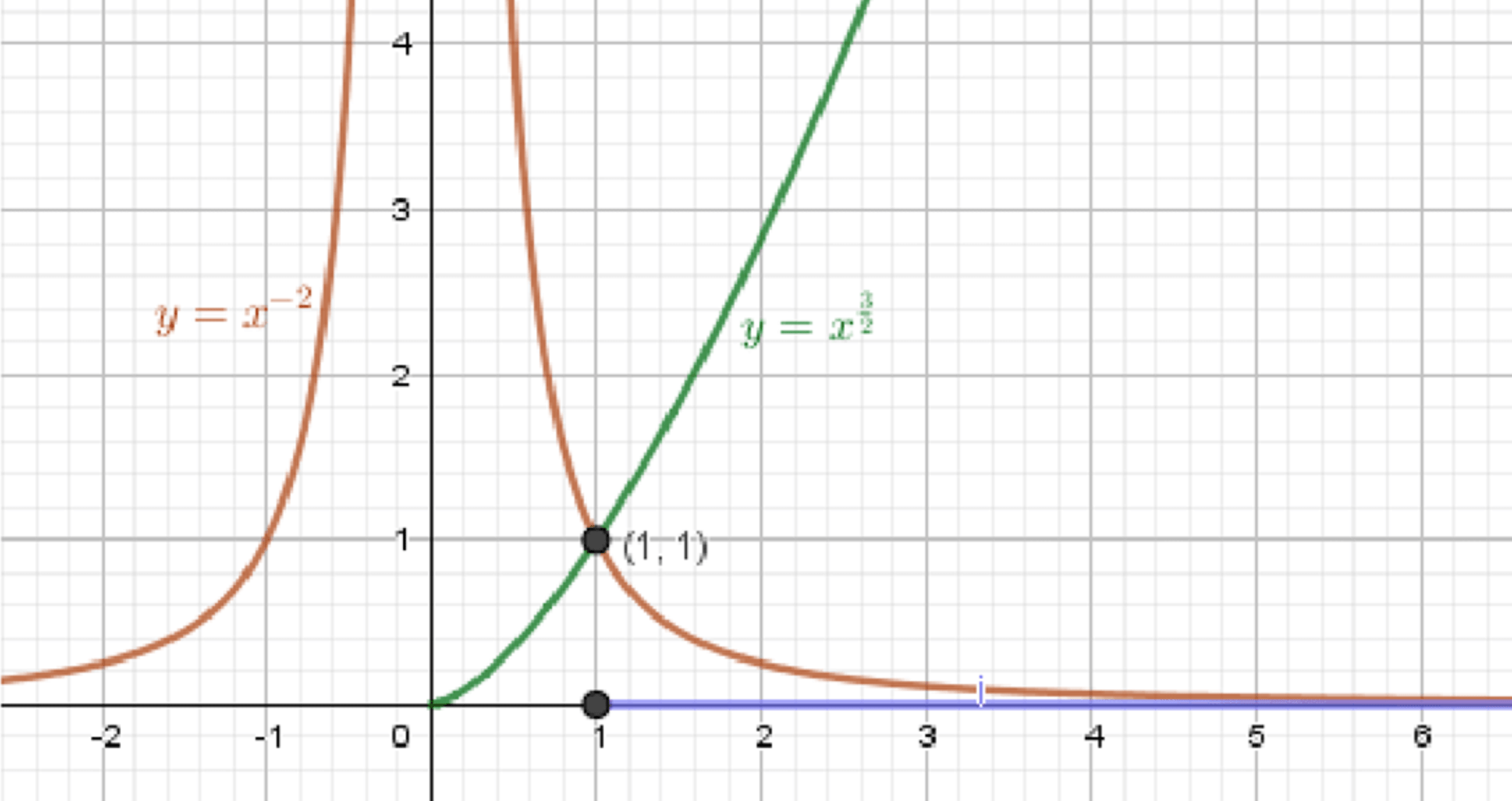
в) ;
– степенная функция:
– степенная функция:
Графики функций:
Ответ: .
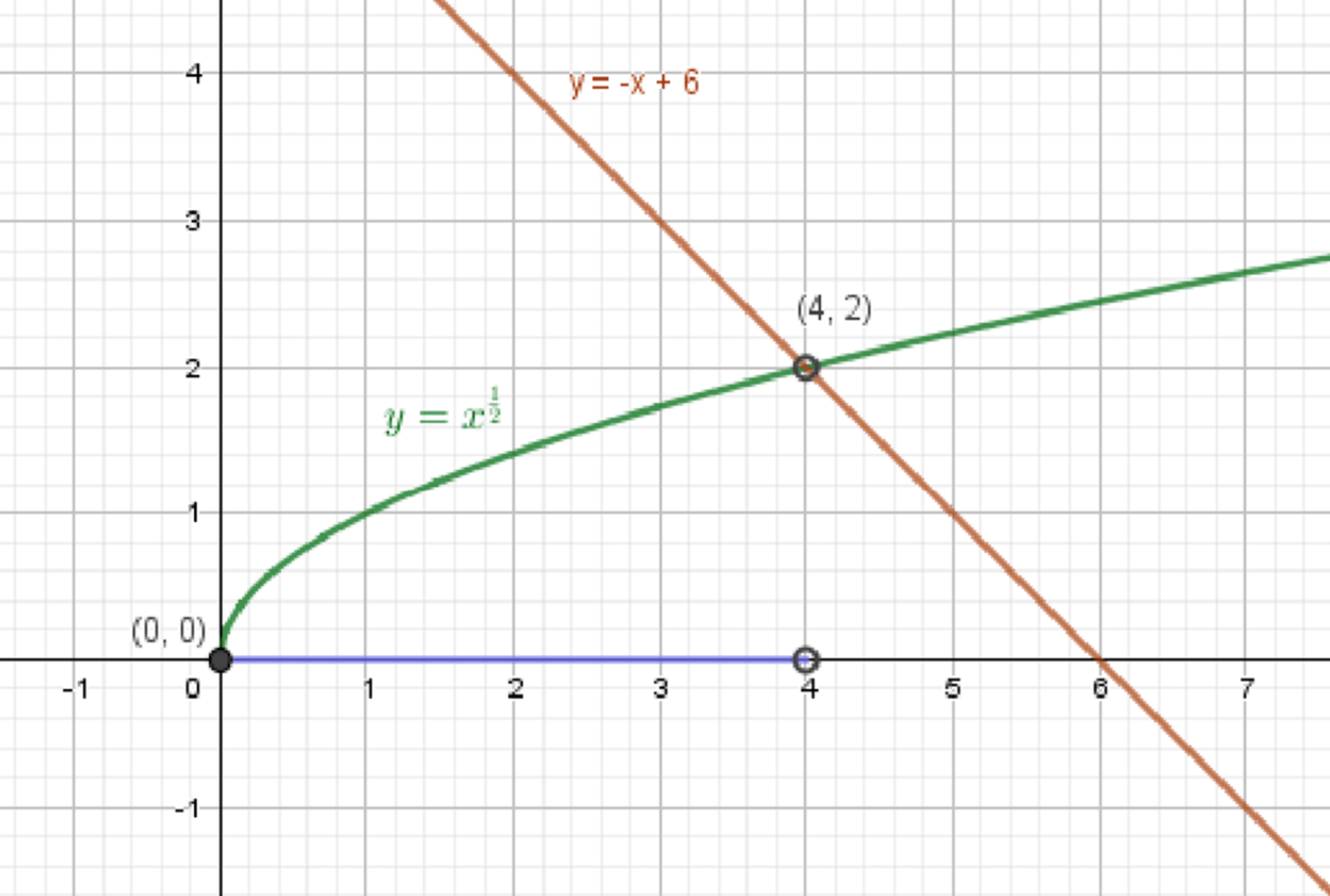
г) ;
– степенная функция:
– уравнение прямой:
Графики функций:
Ответ: .
а)
Неравенство:
Шаг 1: Области определения
- Левая часть: — это корень квадратный, определён при
- Правая часть: — определена при всех
Итог: неравенство имеет смысл при
Шаг 2: Построим графики по точкам
График 1: — это половина параболы, обращённая вверх
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
Гладкая возрастающая кривая, начиная от , без пересечений оси .
График 2: — это прямая с наклоном –1, проходящая через точку (6, 0), пересекающая ось в точке (0, 6)
| 0 | 6 |
| 2 | 4 |
| 4 | 2 |
| 6 | 0 |
Убывающая прямая, пересекает график при
Шаг 3: Найдём точку пересечения
Решим уравнение:
Возведём обе части в квадрат:
Решаем квадратное уравнение:
Подставим в исходное уравнение:
- : подходит
- : — не подходит (ложный корень)
Точка пересечения:
Шаг 4: Исследуем знак неравенства
Ищем, где:
- При : — верно
- При : — верно
- При : — не строго
- При : — не выполняется
Ответ (а):
б)
Неравенство:
Шаг 1: Области определения
- Левая часть: — определена при
- Правая часть: — определена при
Общая область определения:
Шаг 2: Построим графики по точкам
График 1:
| 0 | 0 |
| 1 | 1 |
| 4 | 8 |
Монотонно возрастающая кривая, от 0 вверх.
График 2:
| 0,5 | 4 |
| 1 | 1 |
| 2 | 0.25 |
Монотонно убывающая кривая, стремится к при , к 0 при
Шаг 3: Точка пересечения
Решим уравнение:
Переносим в одну сторону:
Домножим обе части на (в допустимой области ):
Шаг 4: Знак неравенства
- При , например :
, — ложно - При , например :
, — истинно
Ответ (б):
в)
Неравенство:
Шаг 1: Области определения
- Левая часть: — определена при
- Правая часть: — определена при всех
Общая область определения:
Шаг 2: Построим графики по точкам
График 1:
| 0.0625 | 2 |
| 1 | 1 |
| 16 | 0.5 |
Функция убывает на , стремится к при , к 0 при
График 2:
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
Монотонно возрастающая кривая
Шаг 3: Точка пересечения
Решим уравнение:
Шаг 4: Проверка знака
- При :
, но неравенство не выполняется - При :
, выполняется
Ответ (в):
г)
Неравенство:
Шаг 1: Область определения
- — определена при всех
- — определена при всех
Общая область:
Шаг 2: Построим графики
График 1:
- Определён на всей числовой прямой
- Чётная функция
- Минимум при :
- Поведение: кривая, напоминающая «мягкий угол», неотрицательная
| 0 | 0 |
| 1 | 1 |
| 8 | 4 |
График 2:
- Прямая с наклоном +1
- Пересекает ось в
| 4 | 0 |
| 6 | 2 |
Шаг 3: Найдём точку пересечения
Решим:
Подбором:
- — подходит
Точка пересечения:
Шаг 4: Проверим знак
- При : — верно
- При : — верно
- При : — нестрого
Нужны те , где ⇒ строго
Ответ (г):