ГДЗ 10-11 Класс Номер 38.38 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Исследуйте функцию на монотонность и экстремум и постройте её график:

а) $y = \sqrt{x} — x$;

б) $y = x\sqrt{x + 2}$

Исследовать функцию на монотонность и экстремум и построить её график:

а) $y = \sqrt{x} — x$;

Производная функции:

$$y'(x) = (\sqrt{x})’ — (x)’ = \frac{1}{2\sqrt{x}} — 1 = \frac{1 — 2\sqrt{x}}{2\sqrt{x}};$$

Промежуток возрастания:

$$1 — 2\sqrt{x} \geq 0;$$ $$2\sqrt{x} \leq 1;$$ $$\sqrt{x} \leq \frac{1}{2};$$ $$x \leq \frac{1}{4};$$

Выражение имеет смысл при:

$$x \geq 0;$$

Точка максимума:

$$y\left(\frac{1}{4}\right) = \sqrt{\frac{1}{4}} — \frac{1}{4} = \frac{1}{2} — \frac{1}{4} = \frac{1}{4};$$

Координаты некоторых точек:

$$\begin{array}{|c|c|c|c|c|} \hline x & 0 & 1 & 4 & 9 \\ \hline y & 0 & 0 & -2 & -6 \\ \hline \end{array}$$

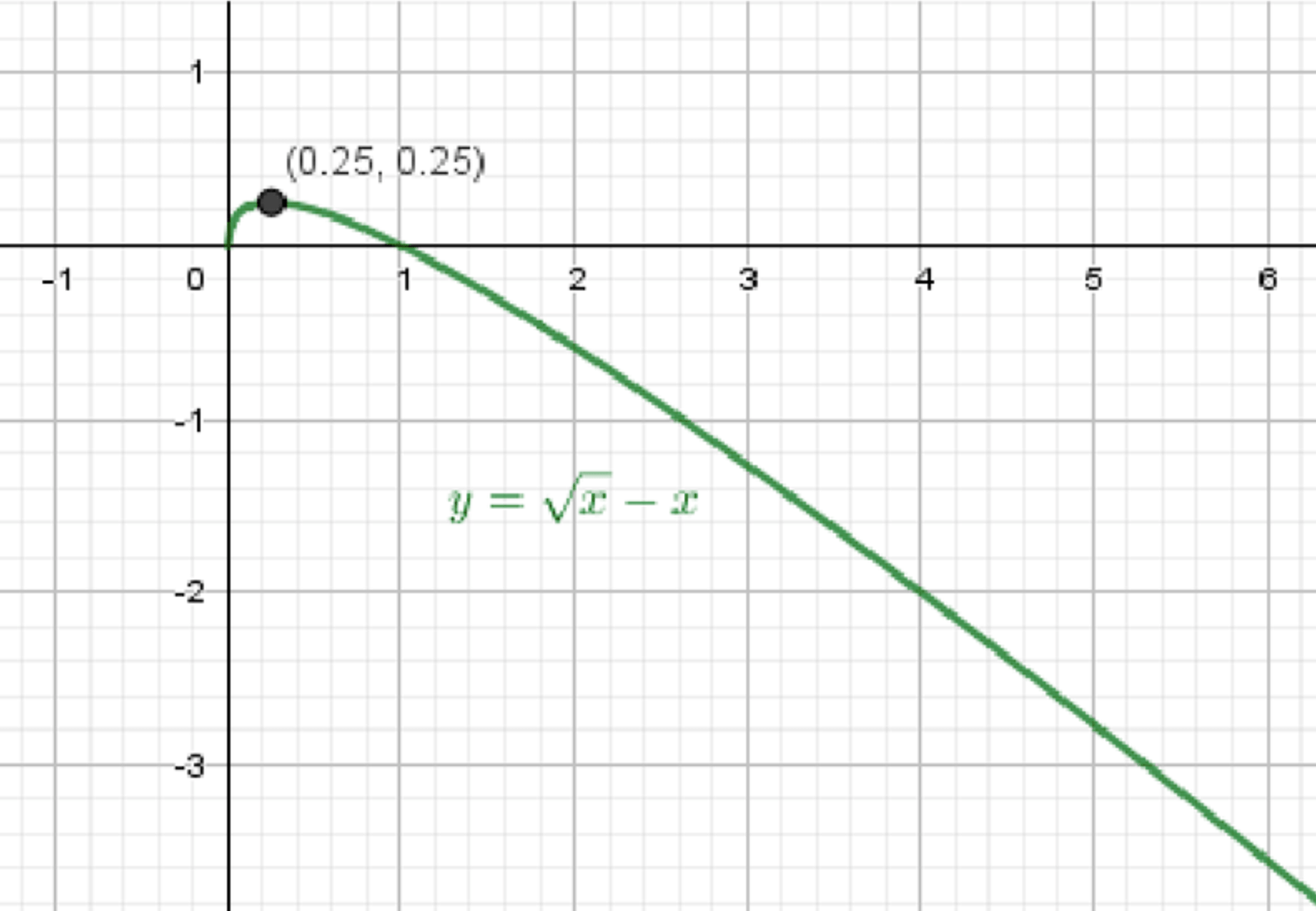
График функции:

Ответ: возрастает на $[0; 0{,}25]$ и убывает на $[0{,}25; +\infty)$;
$x = 0{,}25$ — точка максимума.

б) $y = x\sqrt{x + 2}$;

Производная функции:

$$y'(x) = (x)’ \cdot \sqrt{x + 2} + x \cdot (\sqrt{x + 2})’;$$ $$y'(x) = 1 \cdot \sqrt{x + 2} + x \cdot \frac{1}{2\sqrt{x + 2}} = \frac{2(x + 2) + x}{2\sqrt{x + 2}} = \frac{3x + 4}{2\sqrt{x + 2}};$$

Промежуток возрастания:

$$3x + 4 \geq 0;$$ $$3x \geq -4;$$ $$x \geq -\frac{4}{3};$$

Выражение имеет смысл при:

$$x + 2 \geq 0;$$ $$x \geq -2;$$

Точка минимума:

$$y\left(-\frac{4}{3}\right) = -\frac{4}{3} \cdot \sqrt{-\frac{4}{3} + 2} = -\frac{4}{3} \cdot \sqrt{\frac{2}{3}} = -\frac{4\sqrt{2}}{3\sqrt{3}} = -\frac{4\sqrt{6}}{9};$$

Координаты некоторых точек:

$$\begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 2 \\ \hline y & 0 & -1 & 0 & 4 \\ \hline \end{array}$$

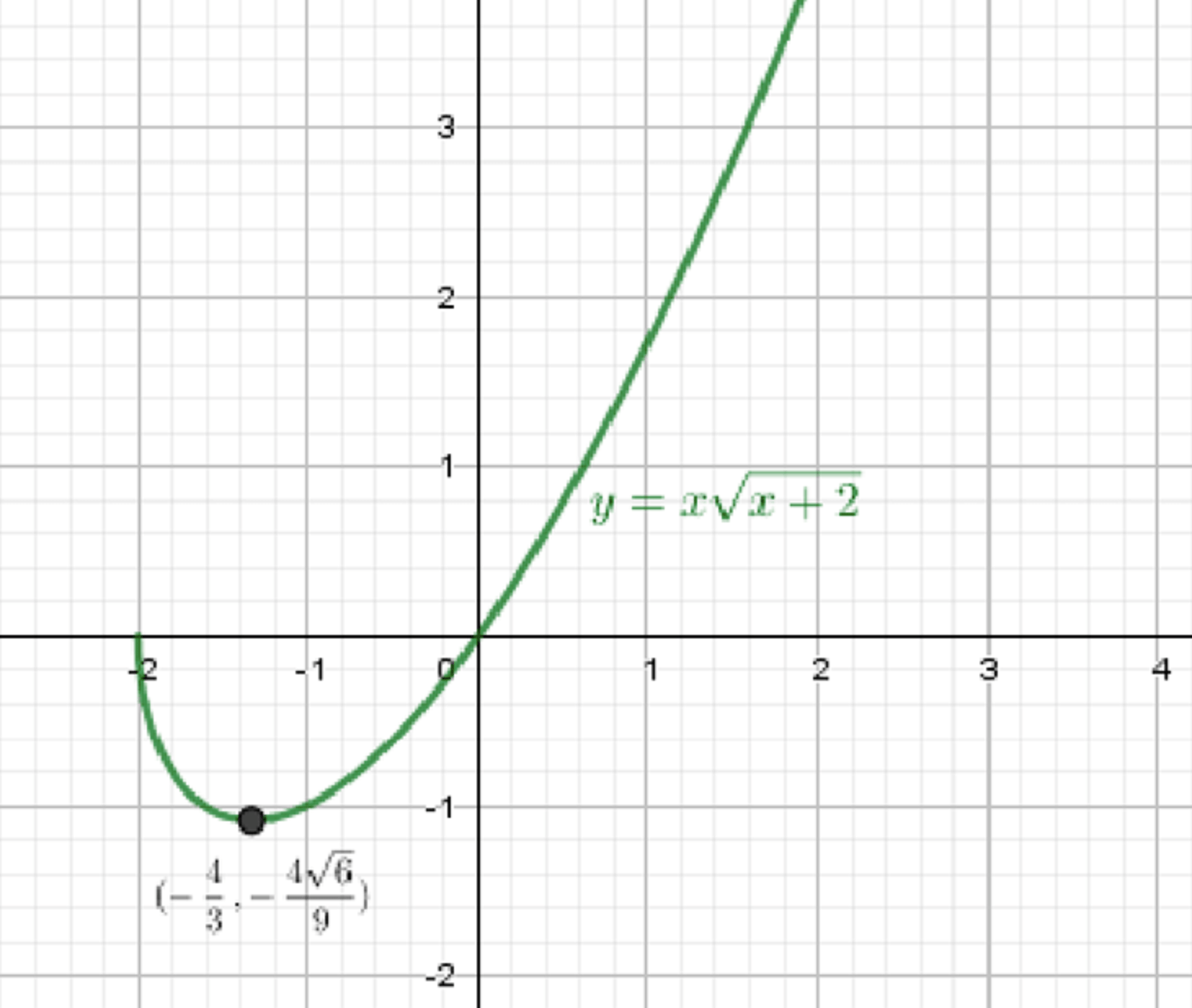
График функции:

Ответ: возрастает на $\left[-\frac{4}{3}; +\infty\right)$ и убывает на $\left[-2; -\frac{4}{3}\right]$;
$x = -\frac{4}{3}$ — точка минимума.

а) $y = \sqrt{x} — x$

1. Область определения функции

Функция содержит корень $\sqrt{x}$, который определён только при $x \geq 0$.
Значит, область определения:

$$x \in [0; +\infty)$$

2. Найдём производную

Функция:

$$y = \sqrt{x} — x = x^{1/2} — x$$

Применим правила дифференцирования:

• $(x^n)’ = n x^{n — 1}$
• $(x)’ = 1$

$$y'(x) = \left(x^{1/2}\right)’ — (x)’ = \frac{1}{2}x^{-1/2} — 1 = \frac{1}{2\sqrt{x}} — 1$$

Приведём к общему знаменателю:

$$y'(x) = \frac{1 — 2\sqrt{x}}{2\sqrt{x}}$$

3. Исследуем знак производной

Найдём нули производной:

$$\frac{1 — 2\sqrt{x}}{2\sqrt{x}} = 0 \Rightarrow 1 — 2\sqrt{x} = 0 \Rightarrow \sqrt{x} = \frac{1}{2} \Rightarrow x = \left(\frac{1}{2}\right)^2 = \frac{1}{4}$$

Знаки производной:

• $x \in (0; \frac{1}{4}) \Rightarrow \sqrt{x} < \frac{1}{2} \Rightarrow y'(x) > 0$
• $x \in (\frac{1}{4}; +\infty) \Rightarrow \sqrt{x} > \frac{1}{2} \Rightarrow y'(x) < 0$

4. Вывод о монотонности

• Возрастает при $x \in [0; \frac{1}{4}]$
• Убывает при $x \in [\frac{1}{4}; +\infty)$

5. Найдём экстремум

Так как производная меняет знак с $+$ на $—$, в точке $x = \frac{1}{4}$ — максимум.

Найдём значение функции:

$$y\left(\frac{1}{4}\right) = \sqrt{\frac{1}{4}} — \frac{1}{4} = \frac{1}{2} — \frac{1}{4} = \frac{1}{4}$$

6. Таблица значений (для построения графика)

$$\begin{array}{|c|c|} \hline x & y = \sqrt{x} — x \\ \hline 0 & 0 \\ 1 & 1 — 1 = 0 \\ 4 & 2 — 4 = -2 \\ 9 & 3 — 9 = -6 \\ \hline \end{array}$$

7. Поведение функции

• На $[0; \frac{1}{4})$: функция растёт.
• В точке $x = \frac{1}{4}$: максимум $y = \frac{1}{4}$
• На $(\frac{1}{4}; +\infty)$: функция убывает.

8. График функции

График состоит из ветви, которая сначала поднимается от точки $(0, 0)$, достигает максимума в $\left( \frac{1}{4}, \frac{1}{4} \right)$, затем убывает и уходит вниз.

9. Итог

• Область определения: $x \in [0; +\infty)$
• Возрастает: $x \in [0; 0.25]$
• Убывает: $x \in [0.25; +\infty)$
• Точка максимума: $x = 0.25$, $y = 0.25$

Ответ:

Функция возрастает на $[0; 0{,}25]$, убывает на $[0{,}25; +\infty)$.
Точка максимума: $x = 0{,}25$, $y = 0{,}25$

б) $y = x\sqrt{x + 2}$

1. Область определения

Подкоренное выражение $x + 2 \geq 0 \Rightarrow x \geq -2$

Область определения:

$$x \in [-2; +\infty)$$

2. Найдём производную

Функция:

$$y = x \cdot \sqrt{x + 2}$$

Это произведение двух функций: $u = x$, $v = \sqrt{x + 2}$

Применим правило производной произведения:

$$y’ = u’v + uv’$$

• $u’ = 1$
• $v = (x + 2)^{1/2} \Rightarrow v’ = \frac{1}{2\sqrt{x + 2}}$

Тогда:

$$y'(x) = 1 \cdot \sqrt{x + 2} + x \cdot \frac{1}{2\sqrt{x + 2}} = \frac{2(x + 2) + x}{2\sqrt{x + 2}} = \frac{3x + 4}{2\sqrt{x + 2}}$$

3. Исследуем знак производной

Знаменатель всегда положителен при $x \geq -2$, так как $\sqrt{x + 2} > 0$, кроме точки $x = -2$, где он равен нулю (граница области определения).

Исследуем знак числителя:

$$3x + 4 \geq 0 \Rightarrow x \geq -\frac{4}{3}$$

4. Вывод о монотонности

• На интервале $x \in [-2; -\frac{4}{3})$: производная < 0 → функция убывает
• В точке $x = -\frac{4}{3}$: производная = 0
• На интервале $x \in [-\frac{4}{3}; +\infty)$: производная > 0 → функция возрастает

5. Найдём экстремум

Точка экстремума: $x = -\frac{4}{3}$. Производная меняется с минуса на плюс → это минимум.

Найдём значение функции в этой точке:

$$y\left(-\frac{4}{3}\right) = -\frac{4}{3} \cdot \sqrt{-\frac{4}{3} + 2} = -\frac{4}{3} \cdot \sqrt{\frac{2}{3}} = -\frac{4\sqrt{2}}{3\sqrt{3}} = -\frac{4\sqrt{6}}{9}$$

6. Таблица значений

$$\begin{array}{|c|c|} \hline x & y = x\sqrt{x + 2} \\ \hline -2 & -2 \cdot \sqrt{0} = 0 \\ -1 & -1 \cdot \sqrt{1} = -1 \\ 0 & 0 \cdot \sqrt{2} = 0 \\ 2 & 2 \cdot \sqrt{4} = 2 \cdot 2 = 4 \\ \hline \end{array}$$

7. Поведение функции

• Убывает на $[-2; -\frac{4}{3}]$
• Возрастает на $[-\frac{4}{3}; +\infty)$
• Минимум: $x = -\frac{4}{3},\ y = -\frac{4\sqrt{6}}{9}$

8. График функции

График имеет минимум в точке $x = -\frac{4}{3}$, плавно возрастает вправо и убывает влево, обрываясь на $x = -2$ (левая граница определения).

Ответ:

Функция убывает на $\left[-2; -\frac{4}{3}\right]$, возрастает на $\left[-\frac{4}{3}; +\infty\right)$;
точка минимума: $x = -\frac{4}{3}$, $y = -\frac{4\sqrt{6}}{9}$