ГДЗ 10-11 Класс Номер 39.13 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Схематично изобразите график показательной функции:

а) $$$y=(\sqrt{2}{)}^x$

б) $$$y={\left(\frac{1}{\pi }\right)}^x$

в) $$$y=(\sqrt{7}{)}^x$

г) $$$y = \left(\frac{1}{\sqrt{6}}\right)^x$

Схематично изобразить график показательной функции:

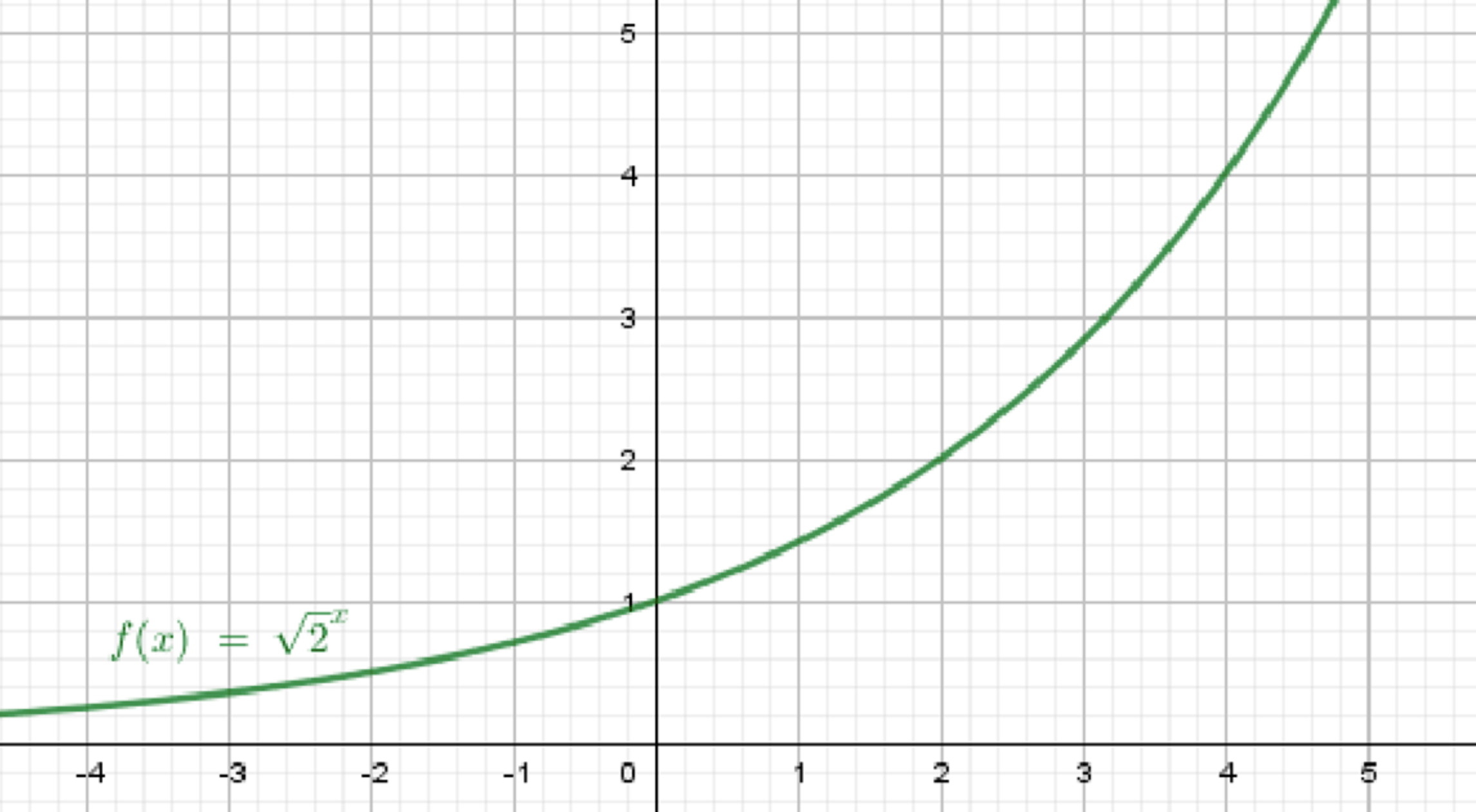
а) $$$y = (\sqrt{2})^x$

Основание степени больше единицы:
$2 > 1$;
$\sqrt{2} > 1$;

График функции:

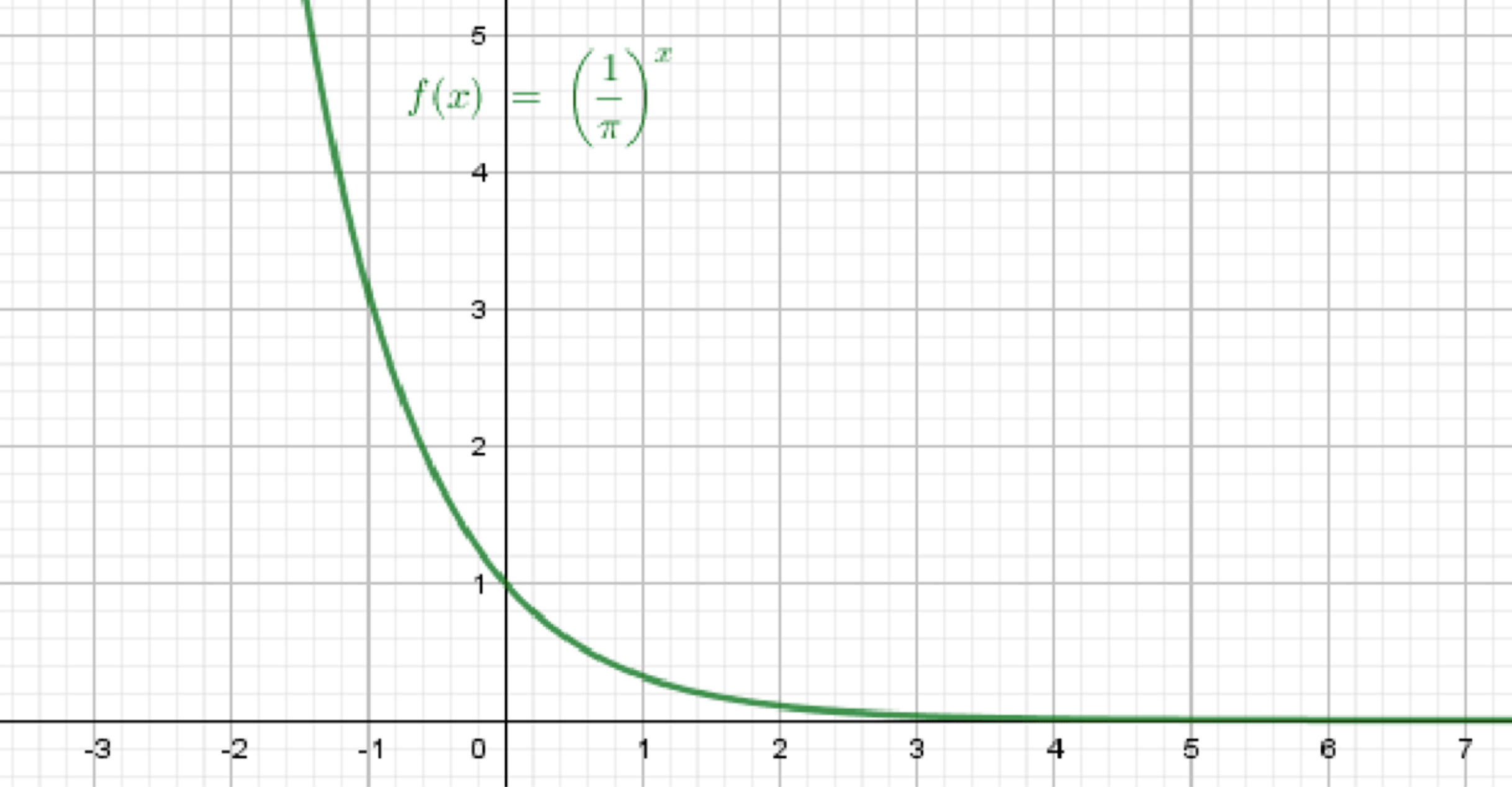
б) $$$y = \left(\frac{1}{\pi}\right)^x$

Основание степени меньше единицы:
$\pi > 1$;
$\frac{1}{\pi} < 1$;

График функции:

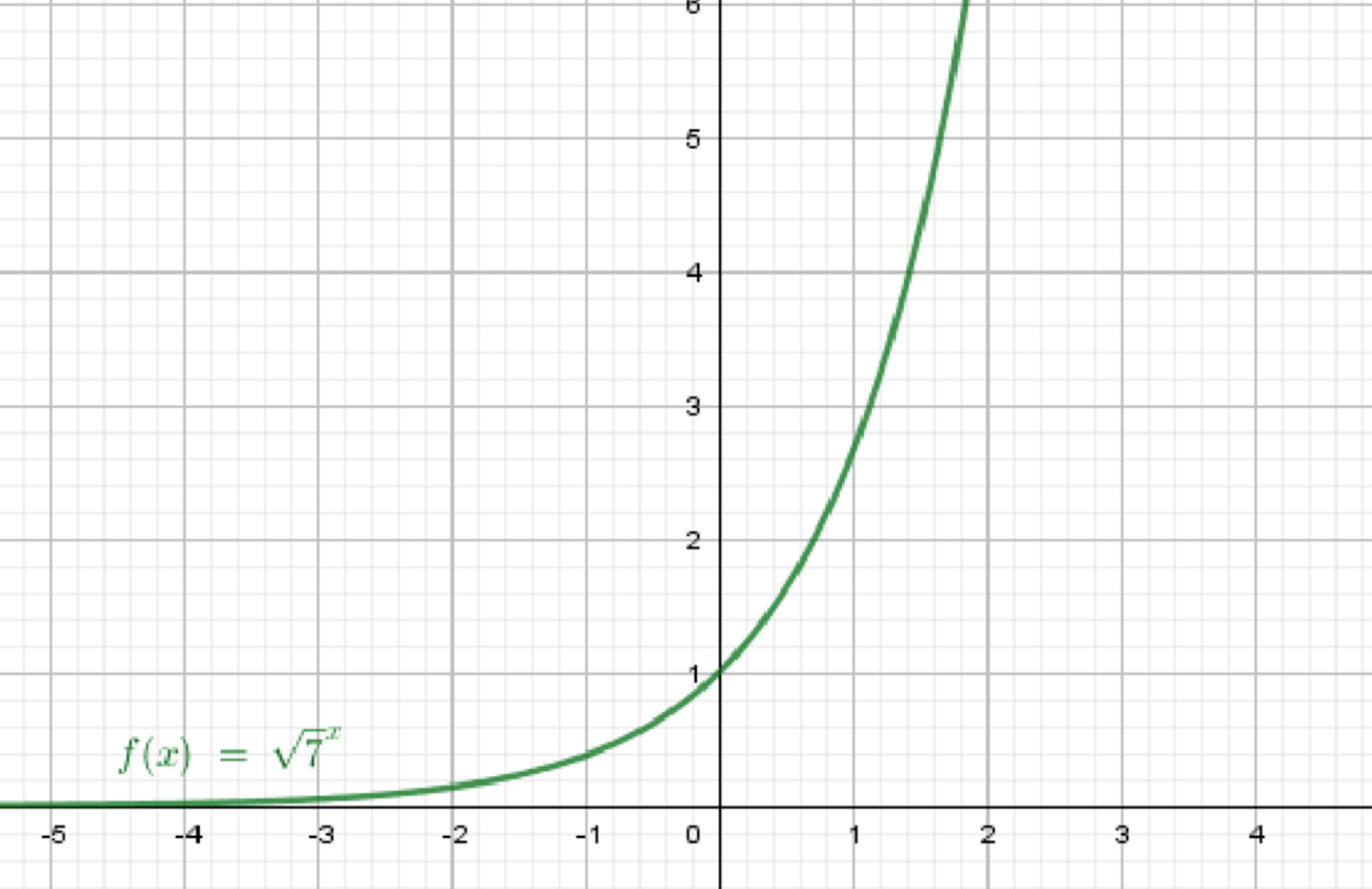
в) $$$y = (\sqrt{7})^x$

Основание степени больше единицы:
$7 > 1$;
$\sqrt{7} > 1$;

График функции:

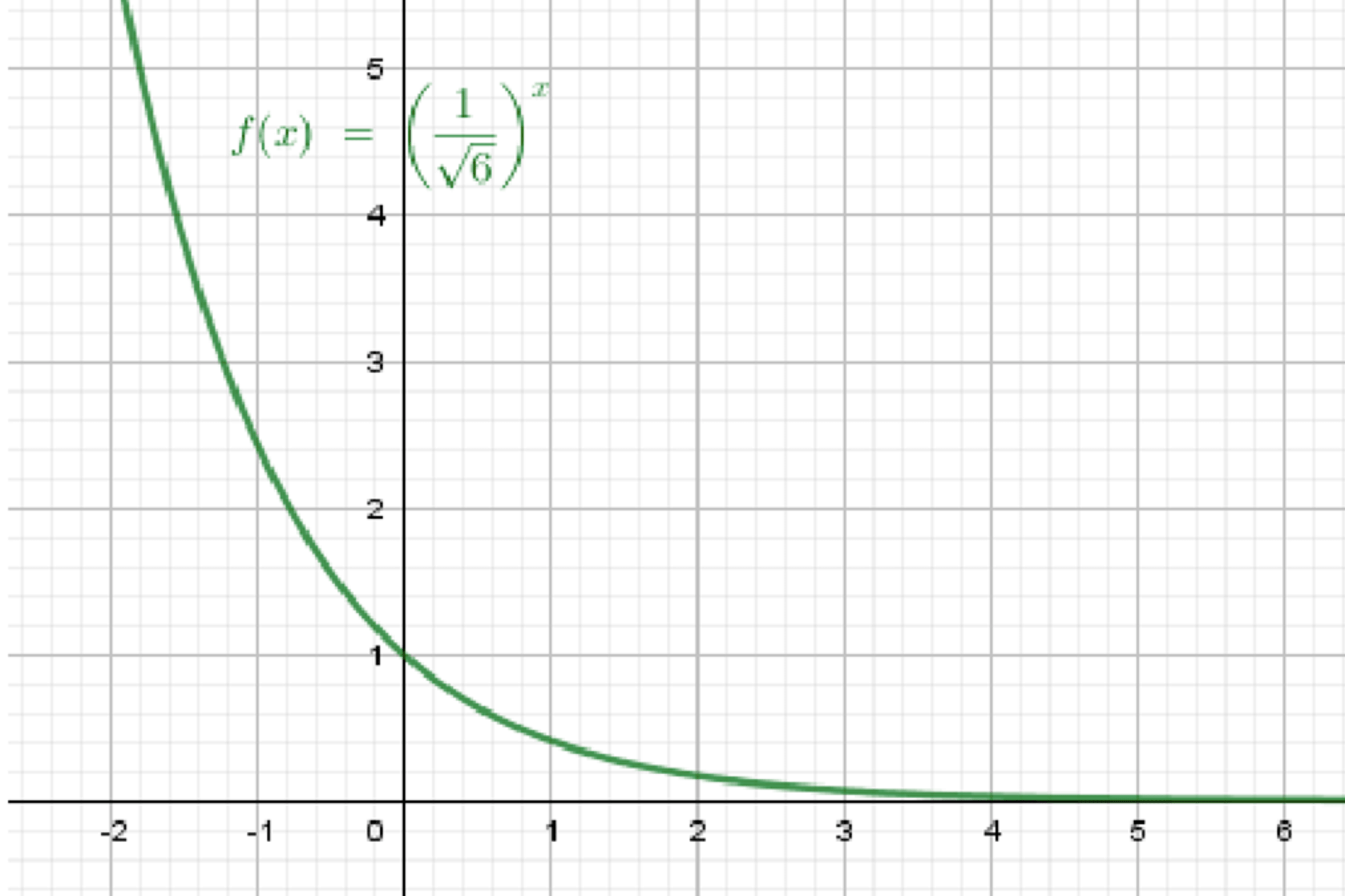
г) $$$y = \left(\frac{1}{\sqrt{6}}\right)^x$

Основание степени меньше единицы:
$6 > 1$;
$\sqrt{6} > 1$;
$\frac{1}{\sqrt{6}} < 1$;

График функции:

Напоминание:

Показательная функция имеет вид

$$y = a^x,$$

где $a > 0$, $a \ne 1$. Её поведение зависит от основания $a$:

• Если $a > 1$: функция возрастает;
• Если $0 < a < 1$: функция убывает.

Общие свойства всех показательных функций $y = a^x$:

1. Область определения: $D(y) = (-\infty; +\infty)$
2. Область значений: $E(y) = (0; +\infty)$
3. Функция не обращается в ноль и не принимает отрицательных значений
4. График не пересекает ось Ox, но асимптотически приближается к ней (горизонтальная асимптота $y = 0$)
5. Проходит через точку $(0; 1)$, так как $a^0 = 1$

а) $y = (\sqrt{2})^x$

Шаг 1. Основание:

$$\sqrt{2} \approx 1{,}414 > 1$$

Значит, функция возрастающая.

Шаг 2. При $x \to -\infty$, $y \to 0$ (приближается к оси $Ox$, но не пересекает её).
При $x \to +\infty$, $y \to +\infty$.

Шаг 3. График расположен выше оси Ox, проходит через точку $(0; 1)$, и с ростом $x$ значения функции стремительно увеличиваются.

Вывод:
График возрастающий, плавно поднимающийся вправо, с асимптотой $y = 0$ слева.

б) $y = \left( \frac{1}{\pi} \right)^x$

Шаг 1. Основание:

$$\pi \approx 3{,}14 > 1 \Rightarrow \frac{1}{\pi} < 1$$

Значит, функция убывающая.

Шаг 2. При $x \to -\infty$, $y \to +\infty$
При $x \to +\infty$, $y \to 0$

Шаг 3. График расположен выше оси Ox, проходит через точку $(0; 1)$, и при увеличении $x$ функция стремится к нулю, но никогда его не достигает.

Вывод:
График убывающий, плавно опускающийся вправо, с асимптотой $y = 0$ справа.

в) $y = (\sqrt{7})^x$

Шаг 1. Основание:

$$\sqrt{7} \approx 2{,}645 > 1$$

Значит, функция возрастающая.

Шаг 2. При $x \to -\infty$, $y \to 0$
При $x \to +\infty$, $y \to +\infty$

Шаг 3. График проходит через точку $(0; 1)$, и при росте $x$ значения быстро увеличиваются. При уменьшении $x$ значения стремятся к нулю.

Вывод:
График возрастающий, сильно поднимающийся вправо, асимптотически приближается к оси $Ox$ слева.

г) $y = \left( \frac{1}{\sqrt{6}} \right)^x$

Шаг 1. Основание:

$$\sqrt{6} \approx 2{,}45 > 1 \Rightarrow \frac{1}{\sqrt{6}} < 1$$

Значит, функция убывающая.

Шаг 2. При $x \to -\infty$, $y \to +\infty$
При $x \to +\infty$, $y \to 0$

Шаг 3. График проходит через точку $(0; 1)$, и при увеличении $x$ убывает, стремясь к нулю.

Вывод:
График убывающий, плавно снижается вправо, асимптотически приближаясь к оси Ox.