ГДЗ 10-11 Класс Номер 39.24 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x) = \begin{cases} 2^x, & \text{если } x \geq 0, \\ 3x + 1, & \text{если } x < 0. \end{cases}$$

а) Вычислите $f(-3);\ f(-2{,}5);\ f(0);\ f(2);\ f(3{,}5);$

б) постройте график функции $y = f(x);$

в) прочитайте график функции.

Дана функция:

$$f(x) = \begin{cases} 2^x, & \text{если } x \geq 0 \\ 3x + 1, & \text{если } x < 0 \end{cases}$$

а) Значения функции:

$$f(-3) = 3 \cdot (-3) + 1 = -9 + 1 = -8;$$ $$f(-2{,}5) = 3 \cdot (-2{,}5) + 1 = -7{,}5 + 1 = -6{,}5;$$ $$f(0) = 2^0 = 1;$$ $$f(2) = 2^2 = 4;$$ $$f(3{,}5) = 2^{3{,}5} = 2^3 \cdot 2^{0{,}5} = 8 \cdot 2^{\frac{1}{2}} = 8\sqrt{2};$$

б) Построить график функции $y = f(x)$:

$y = 3x + 1$ — уравнение прямой:

$y = 2^x$ — показательная функция:

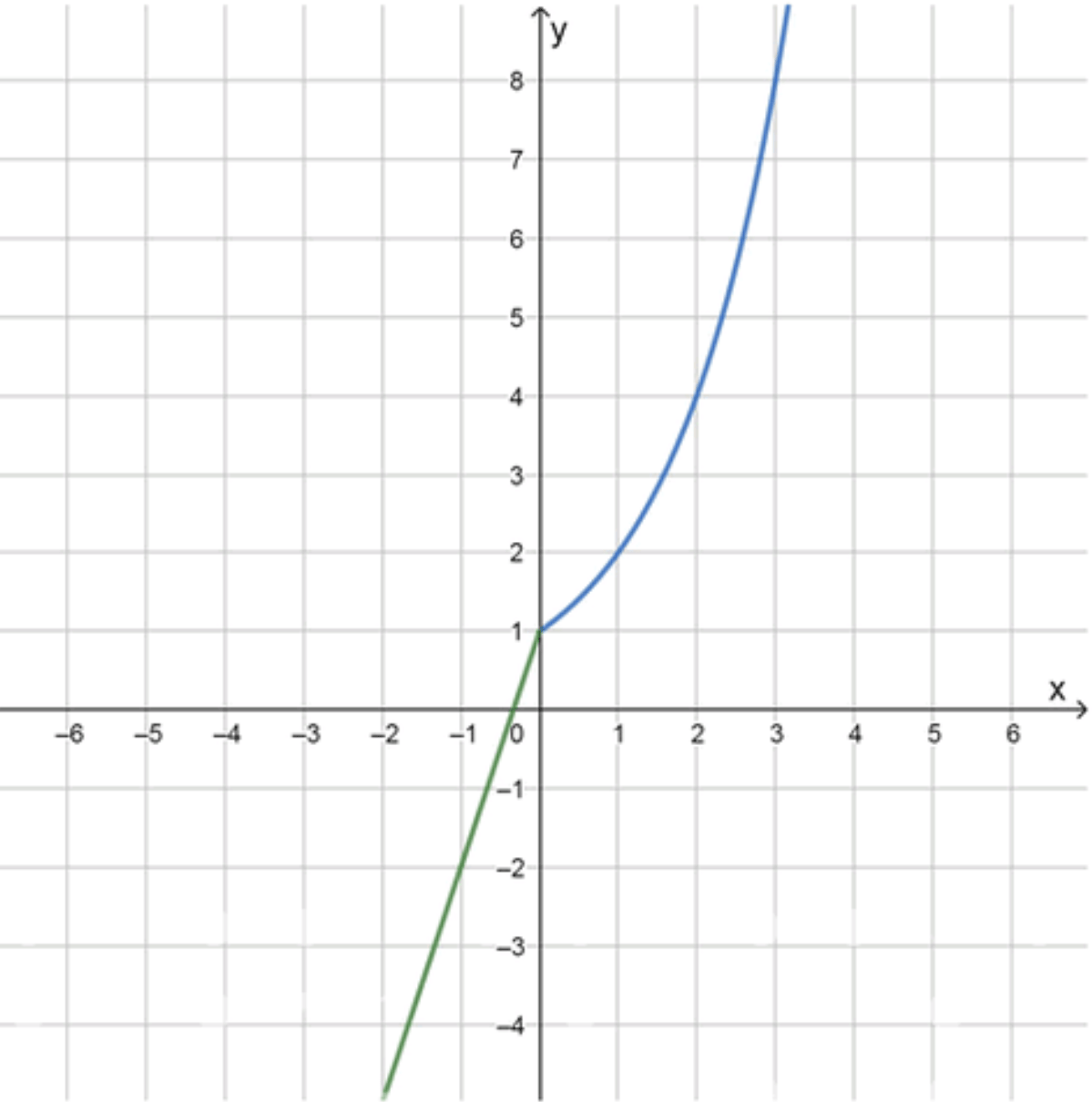
График функции:

в) Свойства функции:

$$D(f) = (-\infty;\ +\infty);$$

Ни чётная, ни нечётная;

Возрастает на всей числовой прямой;

Не ограничена снизу, не ограничена сверху;

$y_{\text{наим}}$ — не существует, $y_{\text{наиб}}$ — не существует;

Непрерывна на всей области определения;

$$E(f) = (-\infty;\ +\infty);$$

Функция дифференцируема во всех точках, кроме $x = 0$.

Дана функция:

$$f(x) = \begin{cases} 2^x, & \text{если } x \geq 0 \\ 3x + 1, & \text{если } x < 0 \end{cases}$$

а) Вычисление значений функции

В этой функции два разных выражения, которые используются в зависимости от значения $x$:

• Если $x \geq 0$, используем показательную функцию $f(x) = 2^x$
• Если $x < 0$, используем линейную функцию $f(x) = 3x + 1$

1. $f(-3)$

• $-3 < 0$, значит:

$$f(-3) = 3 \cdot (-3) + 1 = -9 + 1 = \boxed{-8}$$

2. $f(-2{,}5)$

• $-2{,}5 < 0$, значит:

$$f(-2{,}5) = 3 \cdot (-2{,}5) + 1 = -7{,}5 + 1 = \boxed{-6{,}5}$$

3. $f(0)$

• $0 \geq 0$, значит:

$$f(0) = 2^0 = \boxed{1}$$

4. $f(2)$

• $2 \geq 0$, значит:

$$f(2) = 2^2 = \boxed{4}$$

5. $f(3{,}5)$

• $3{,}5 \geq 0$, значит:

$$f(3{,}5) = 2^{3{,}5} = 2^3 \cdot 2^{0{,}5} = 8 \cdot 2^{\frac{1}{2}} = 8 \cdot \sqrt{2} \approx 8 \cdot 1{,}4142 \approx \boxed{11{,}3136}$$

б) Построение графика функции $y = f(x)$

1. Построение для $x < 0$: линейная функция $y = 3x + 1$

Построим таблицу значений:

Для $x = 0$ правая граница, точка принадлежит другой части функции, но важно, что обе части сходятся к $y = 1$

График — прямая линия, проходящая через, например, точки:

• $(-1;\ -2)$
• $(0;\ 1)$

2. Построение для $x \geq 0$: показательная функция $y = 2^x$

Построим таблицу значений:

Дополнительные точки (по желанию):

• $x = 3{,}5 \Rightarrow y = 8\sqrt{2} \approx 11{,}31$

График — возрастающая кривая, стремящаяся к 0 при $x \to -\infty$, но у нас она начинается с $x = 0$

Плавность графика в точке $x = 0$:

Проверим совпадение значений в точке $x = 0$:

• Слева: $3x + 1 \rightarrow 3 \cdot 0 + 1 = 1$
• Справа: $2^0 = 1$

Значения совпадают, значит график непрерывен в точке $x = 0$

в) Свойства функции $f(x)$

1. Область определения $D(f)$:

• Оба выражения определены при всех значениях $x$
• Значит, функция определена при всех $x \in \mathbb{R}$

$$D(f) = (-\infty;\ +\infty)$$

2. Чётность функции:

Проверим, является ли функция чётной или нечётной:

• $f(-x) \ne f(x)$
• $f(-x) \ne -f(x)$

Значит, функция не чётная и не нечётная

3. Монотонность:

• Для $x < 0$: $f(x) = 3x + 1$ — линейная с положительным коэффициентом ⇒ возрастает
• Для $x \geq 0$: $f(x) = 2^x$ — показательная с $a > 1$ ⇒ возрастает

Функция возрастает на всей числовой прямой

4. Ограниченность:

• При $x \to -\infty$: $f(x) = 3x + 1 \to -\infty$
• При $x \to +\infty$: $f(x) = 2^x \to +\infty$

Функция:

• не ограничена снизу
• не ограничена сверху

5. Наименьшее и наибольшее значения:

• Функция убывает и возрастает без границ ⇒

$$y_{\text{наим}} — \text{не существует};\quad y_{\text{наиб}} — \text{не существует}$$

6. Непрерывность:

• Обе части функции непрерывны
• В точке $x = 0$ переход плавный: значения совпадают

Значит, функция непрерывна на всей области определения

7. Область значений $E(f)$:

• $y \to -\infty$ при $x \to -\infty$
• $y \to +\infty$ при $x \to +\infty$

$$E(f) = (-\infty;\ +\infty)$$

8. Дифференцируемость:

• Для $x < 0$: $f(x) = 3x + 1 \Rightarrow f'(x) = 3$
• Для $x > 0$: $f(x) = 2^x \Rightarrow f'(x) = 2^x \ln 2$

Проверим дифференцируемость в точке $x = 0$:

• Слева: $f’_-(0) = 3$
• Справа: $f’_+(0) = 2^0 \cdot \ln 2 = \ln 2 \approx 0{,}693$

Производные не совпадают, ⇒ функция не дифференцируема в точке $x=0$$x = 0$