ГДЗ 10-11 Класс Номер 39.25 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x) = \begin{cases} 4^x, \text{ если } x < 1, \\ -x^2 + 1, \text{ если } x \geq 1. \end{cases}$$

а) Вычислите $f(-3);\ f(-2{,}5);\ f(0);\ f(1);\ f(2);$

б) постройте график функции $y = f(x);$

в) прочитайте график функции.

Дана функция:

$$f(x) = \begin{cases} 4^x, \text{ если } x < 1 \\ -x^2 + 1, \text{ если } x \geq 1 \end{cases}$$

а) Значения функции:

$$f(-3) = 4^{-3} = \left( \frac{1}{4} \right)^3 = \frac{1}{64};$$ $$f(-2{,}5) = 4^{-2{,}5} = (2^2)^{-2{,}5} = 2^{-5} = \frac{1}{2^5} = \frac{1}{32};$$ $$f(0) = 4^0 = 1;$$ $$f(1) = -1^2 + 1 = -1 + 1 = 0;$$ $$f(2) = -2^2 + 1 = -4 + 1 = -3;$$

б) Построить график функции $y = f(x)$:

$y = 4^x$ — показательная функция:

$y = -x^2 + 1$ — уравнение параболы:

График функции:

в) Свойства функции:

$$D(f) = (-\infty;\ +\infty);$$

Ни чётная, ни нечётная;

Возрастает на луче $(-\infty;\ 1)$ и убывает на луче $[1;\ +\infty)$;

Имеет горизонтальную асимптоту $\lim\limits_{x \to -\infty} f(x) = 0$;

Не ограничена снизу, ограничена сверху;

$y_{\text{наим}}$ — не существует, $y_{\text{наиб}}$ — не существует;

Непрерывна на интервалах $(-\infty;\ 1) \cup (1;\ +\infty)$;

$$E(f) = (-\infty;\ 4);$$

Функция дифференцируема всюду, кроме точки $x = 1$.

Дана функция:

$$f(x) = \begin{cases} 4^x, \quad \text{если } x < 1 \\ -x^2 + 1, \quad \text{если } x \geq 1 \end{cases}$$

а) Вычисление значений функции

Анализ:

Функция задана по частям:

• Если $x < 1$, то $f(x) = 4^x$
• Если $x \geq 1$, то $f(x) = -x^2 + 1$

1. $f(-3)$

• $-3 < 1 \Rightarrow f(x) = 4^x$

$$f(-3) = 4^{-3} = \left(\frac{1}{4}\right)^3 = \frac{1}{64}$$

2. $f(-2{,}5)$

• $-2{,}5 < 1 \Rightarrow f(x) = 4^x$

$$f(-2{,}5) = 4^{-2{,}5} = (2^2)^{-2{,}5} = 2^{-5} = \frac{1}{2^5} = \frac{1}{32}$$

3. $f(0)$

• $0 < 1 \Rightarrow f(x) = 4^x$

$$f(0) = 4^0 = 1$$

4. $f(1)$

• $1 \geq 1 \Rightarrow f(x) = -x^2 + 1$

$$f(1) = -1^2 + 1 = -1 + 1 = 0$$

5. $f(2)$

• $2 \geq 1 \Rightarrow f(x) = -x^2 + 1$

$$f(2) = -2^2 + 1 = -4 + 1 = -3$$

Ответ к пункту а):

$$f(-3)=\frac{1}{64};f(-\mathrm{2,5})=\frac{1}{32};f(0)=1;$$

$$f(-3) = \frac{1}{64};\quad f(-2{,}5) = \frac{1}{32};\quad f(0) = 1;\quad f(1) = 0;\quad f(2) = -3$$

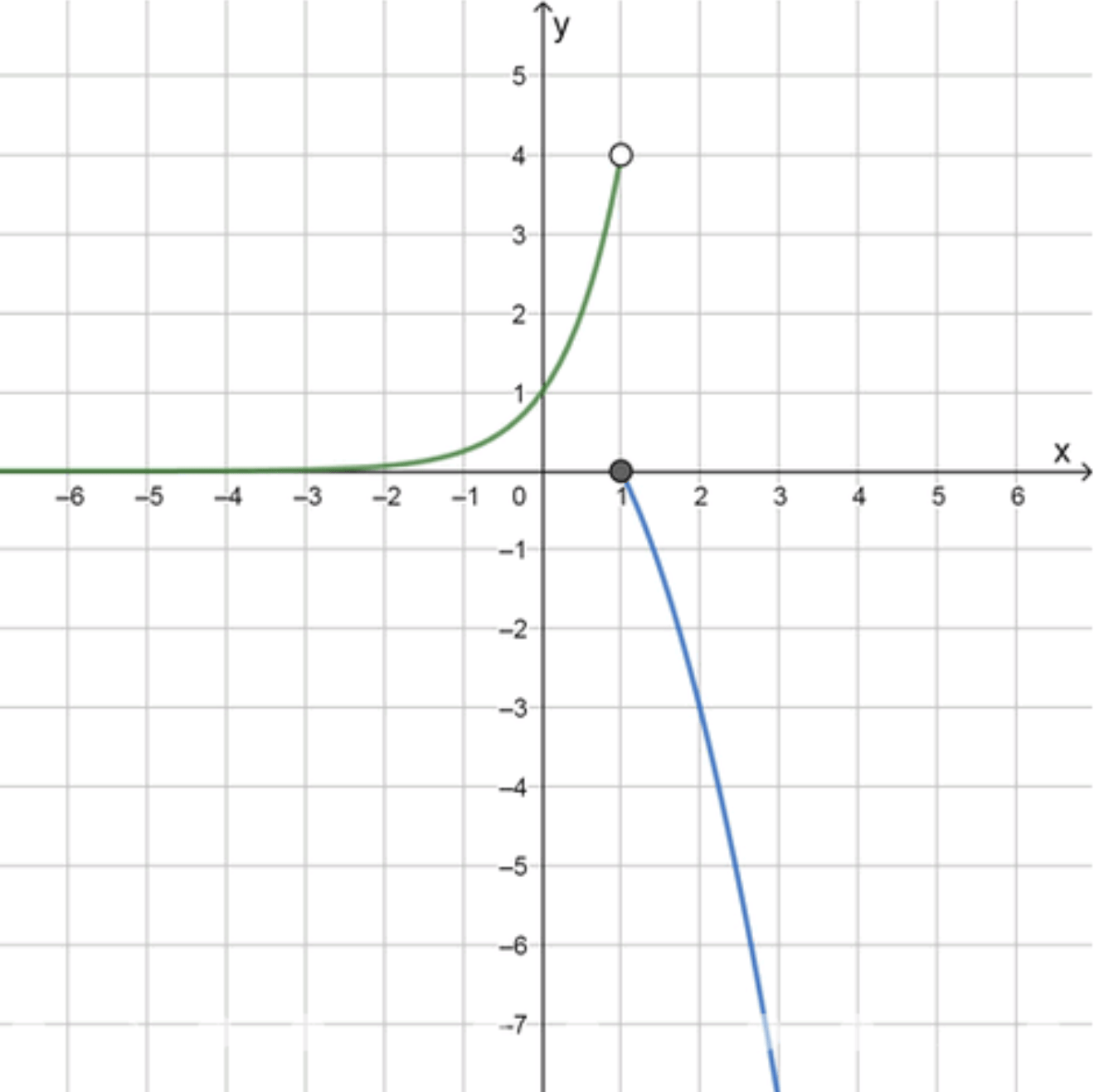
б) Построение графика функции

1. График $y = 4^x$, при $x < 1$

Это показательная функция с основанием $4 > 1$.
Свойства:

• Возрастает
• При $x \to -\infty$, $y \to 0$
• Проходит через точку $(0;\ 1)$
• Не определена при $x = 1$, но можно найти значение вблизи:
  $4^{0{,}9} \approx 3{,}48$, $4^{0{,}99} \approx 3{,}96$

• На графике точка при $x = 1$ — вырезанная, т.к. $x < 1$

2. График $y = -x^2 + 1$, при $x \geq 1$

Это парабола, ветви направлены вниз (коэффициент при $x^2$ отрицателен)

• Вершина: $x = 0$, но используется только ветвь при $x \geq 1$
• Построим таблицу:

• График начинается в точке $(1;\ 0)$ — эта точка включается (замкнутая)

Гладкость графика в точке $x = 1$

• Слева: $\lim\limits_{x \to 1^-} 4^x = 4$
• Справа: $f(1) = 0$

Значения не совпадают ⇒ график разрывный в точке $x = 1$

в) Свойства функции

1. Область определения $D(f)$

• Оба выражения определены на всей числовой прямой

$$D(f) = (-\infty;\ +\infty)$$

2. Чётность / нечётность

Проверим:

• $f(-x) \ne f(x)$
• $f(-x) \ne -f(x)$

Пример:

• $f(-1) = 4^{-1} = \frac{1}{4}$
• $f(1) = 0$

Разные значения ⇒ функция нечётная и не чётная

3. Монотонность

• На интервале $(-\infty;\ 1)$: $f(x) = 4^x$ — возрастает
• На интервале $[1;\ +\infty)$: $f(x) = -x^2 + 1$ — убывает

$$f(x) \uparrow \text{ на } (-\infty;\ 1), \quad f(x) \downarrow \text{ на } [1;\ +\infty)$$

4. Асимптота

Показательная часть $4^x$ при $x \to -\infty$ стремится к 0:

$$\lim\limits_{x \to -\infty} f(x) = 0$$

⇒ горизонтальная асимптота $y = 0$

5. Ограниченность

• Снизу: $f(x) \to -\infty$ при $x \to +\infty$ (из-за параболы)
• Сверху: наибольшее значение — предел слева в точке разрыва, но он не достигается:

  $$\lim_{x \to 1^-} f(x) = 4, \quad f(1) = 0$$

Максимальное значение не достигается ⇒

• Не ограничена снизу
• Ограничена сверху (по значению функции, но точной границы нет)

6. Наименьшее и наибольшее значения

• Функция уходит в минус бесконечность ⇒ наименьшего значения нет
• Значение 4 (предел при $x \to 1^-$) не входит ⇒ наибольшего значения тоже нет

7. Непрерывность

• $f(x) = 4^x$ — непрерывна на $(-\infty;\ 1)$
• $f(x) = -x^2 + 1$ — непрерывна на $[1;\ +\infty)$
• В точке $x = 1$ — разрыв

$$\text{Непрерывна на } (-\infty;\ 1) \cup (1;\ +\infty)$$

8. Область значений $E(f)$

• Показательная часть $4^x$ при $x < 1$ принимает значения от $0$ (асимптотически) до почти $4$, но $x = 1$ не включается ⇒ $y < 4$
• Ветвь параболы убывает от $f(1) = 0$ до $-\infty$

⇒ Значения функции лежат в:

$$E(f) = (-\infty;\ 4)$$

9. Дифференцируемость

• $f(x)$ — гладкая в каждой части (степенная и многочлен)
• В точке $x = 1$:

$$f’_-(1) = \frac{d}{dx} 4^x = 4^x \ln 4 = 4 \ln 4 \approx 5{,}545$$ $$f’_+(1) = \frac{d}{dx} (-x^2 + 1) = -2x = -2$$

Производные не равны ⇒ не дифференцируема в точке $x=1$$x = 1$