Краткий ответ:
Решить графически уравнение:
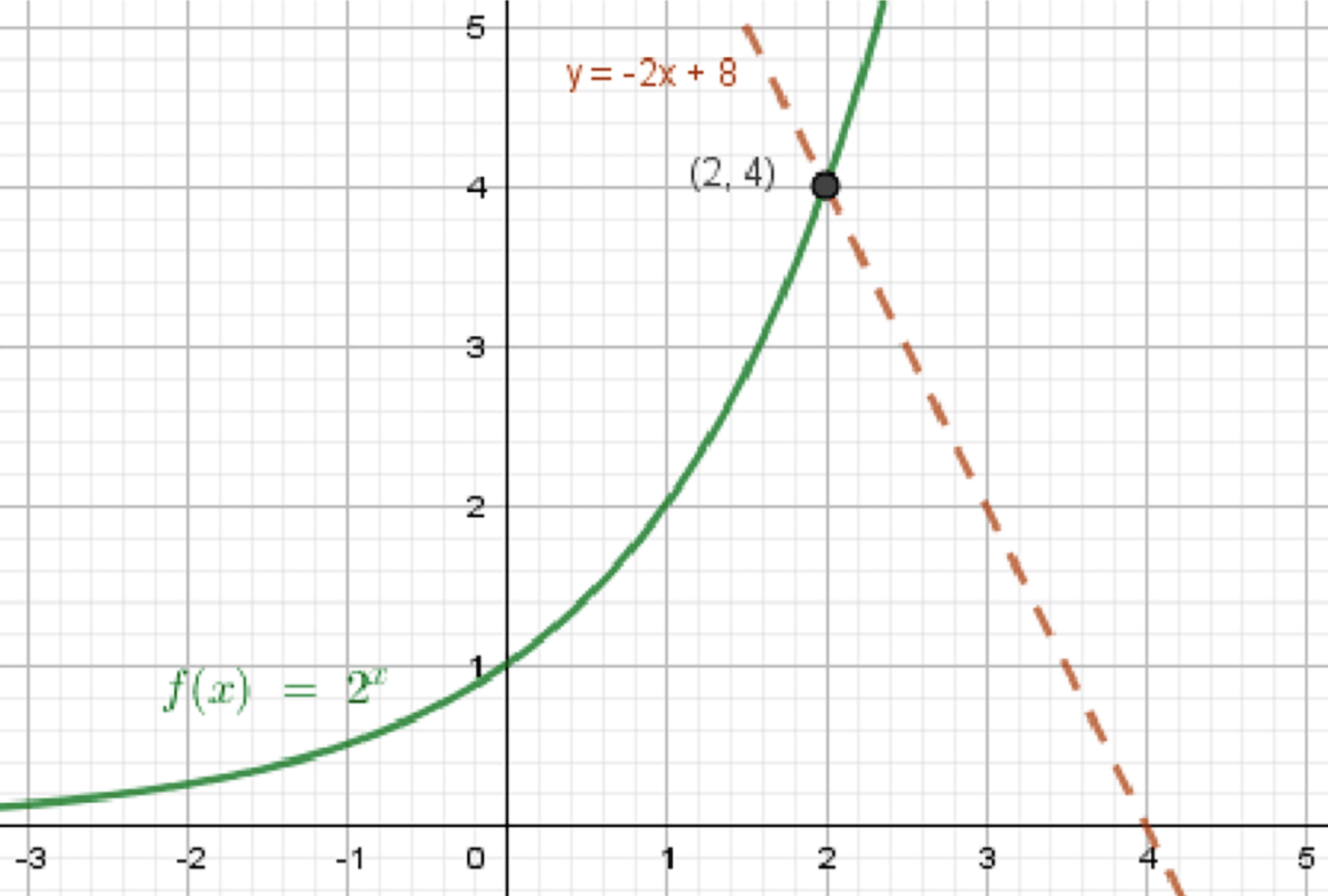
а) 2 x = − 2 x + 8 2^x = -2x + 8 y = 2 x y = 2^x
x 0 2 3 y 1 4 8 \begin{array}{|c|c|c|c|} \hline x & 0 & 2 & 3 \\ \hline y & 1 & 4 & 8 \\ \hline \end{array}
y = − 2 x + 8 y = -2x + 8
x 0 4 y 8 0 \begin{array}{|c|c|c|} \hline x & 0 & 4 \\ \hline y & 8 & 0 \\ \hline \end{array}
Графики функций:
Ответ: x = 2 x = 2
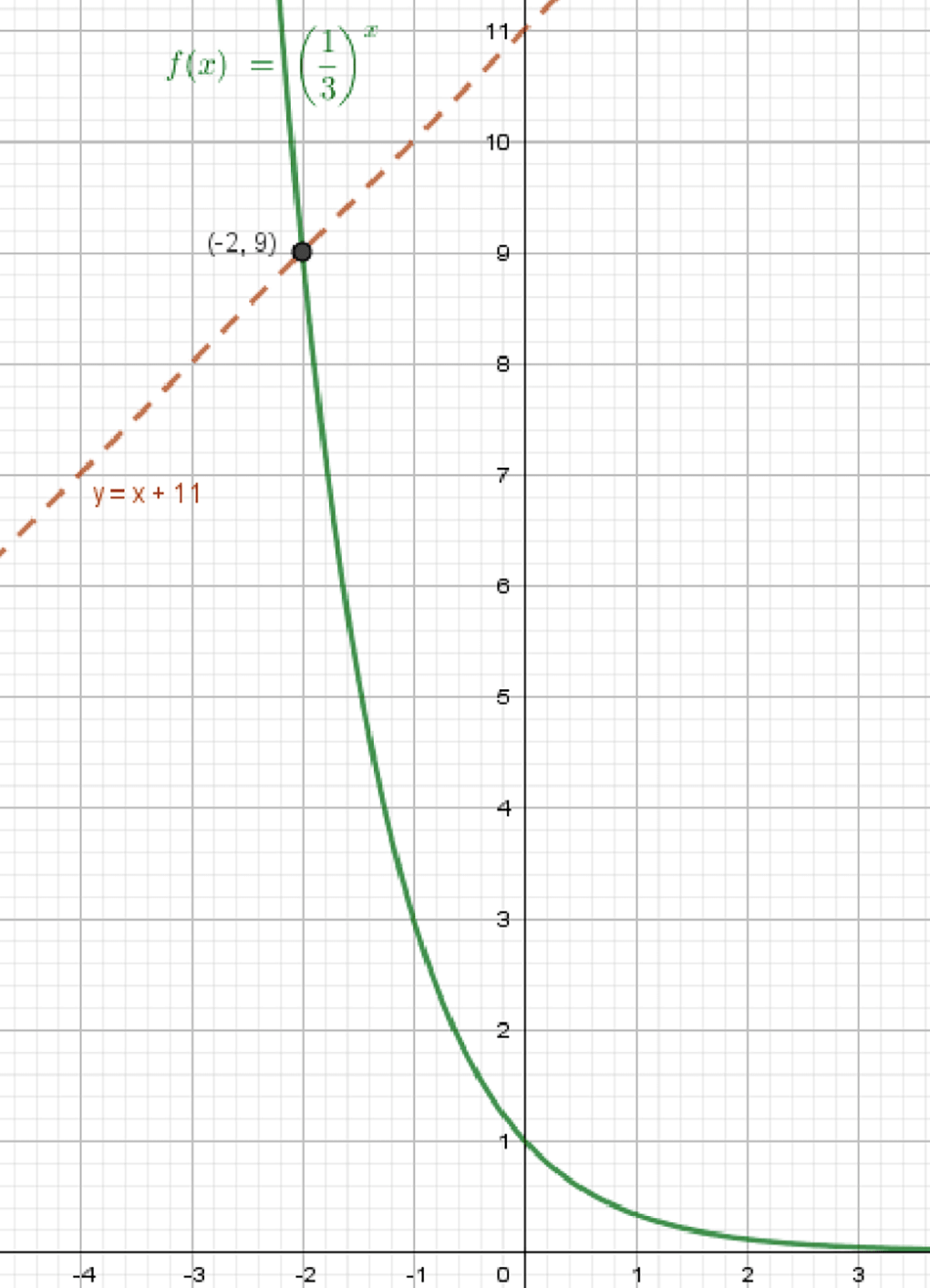
б) ( 1 3 ) x = x + 11 \left(\frac{1}{3}\right)^x = x + 11 y = ( 1 3 ) x y = \left(\frac{1}{3}\right)^x
x − 2 − 1 0 y 9 3 1 \begin{array}{|c|c|c|c|} \hline x & -2 & -1 & 0 \\ \hline y & 9 & 3 & 1 \\ \hline \end{array}
y = x + 11 y = x + 11
x − 4 0 y 7 11 \begin{array}{|c|c|c|} \hline x & -4 & 0 \\ \hline y & 7 & 11 \\ \hline \end{array}
Графики функций:
Ответ: x = − 2 x = -2
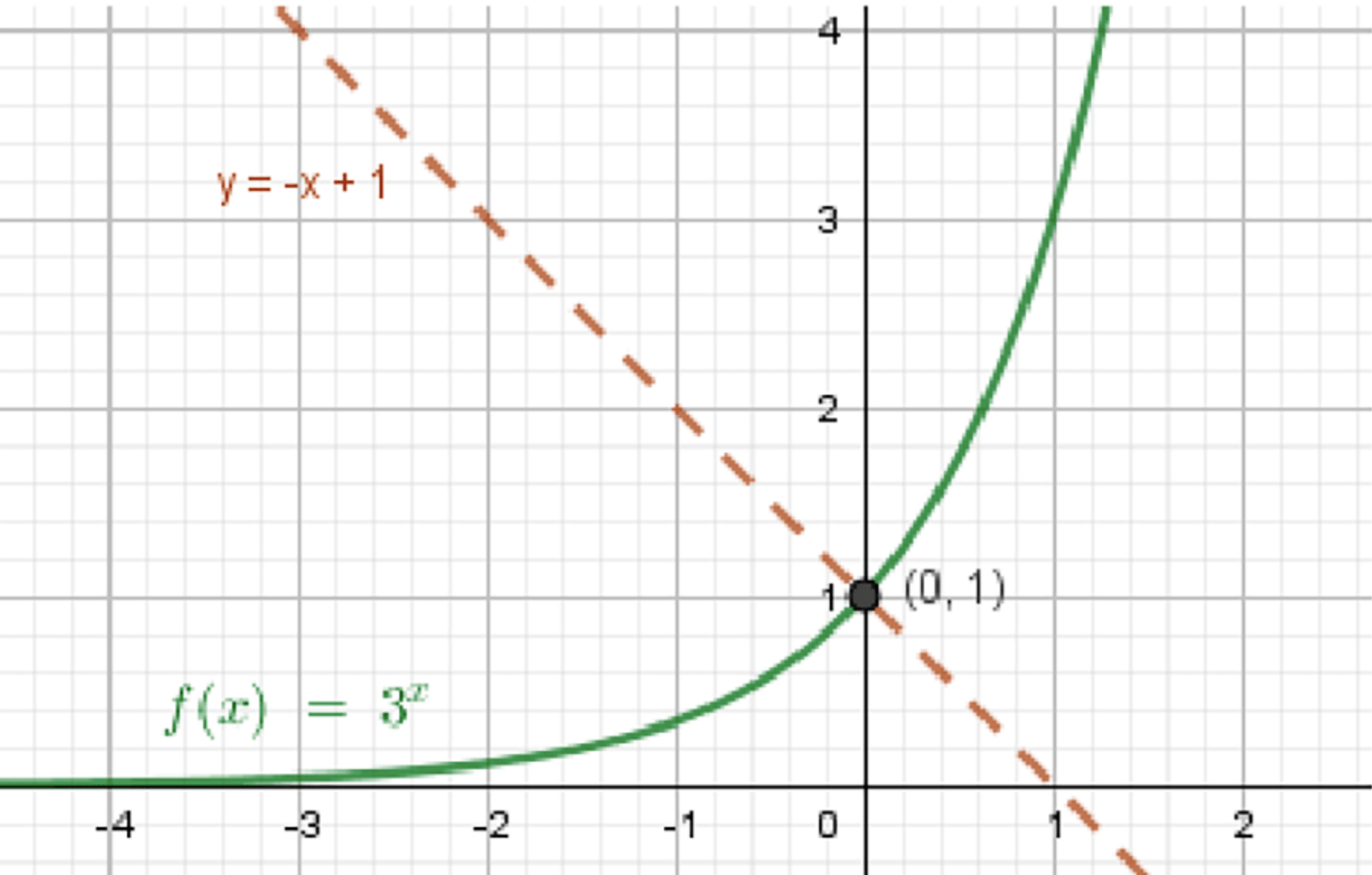
в) 3 x = − x + 1 3^x = -x + 1 y = 3 x y = 3^x
x 0 1 2 y 1 3 9 \begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 1 & 3 & 9 \\ \hline \end{array}
y = − x + 1 y = -x + 1
x − 2 0 y 3 1 \begin{array}{|c|c|c|} \hline x & -2 & 0 \\ \hline y & 3 & 1 \\ \hline \end{array}
Графики функций:
Ответ: x = 0 x = 0
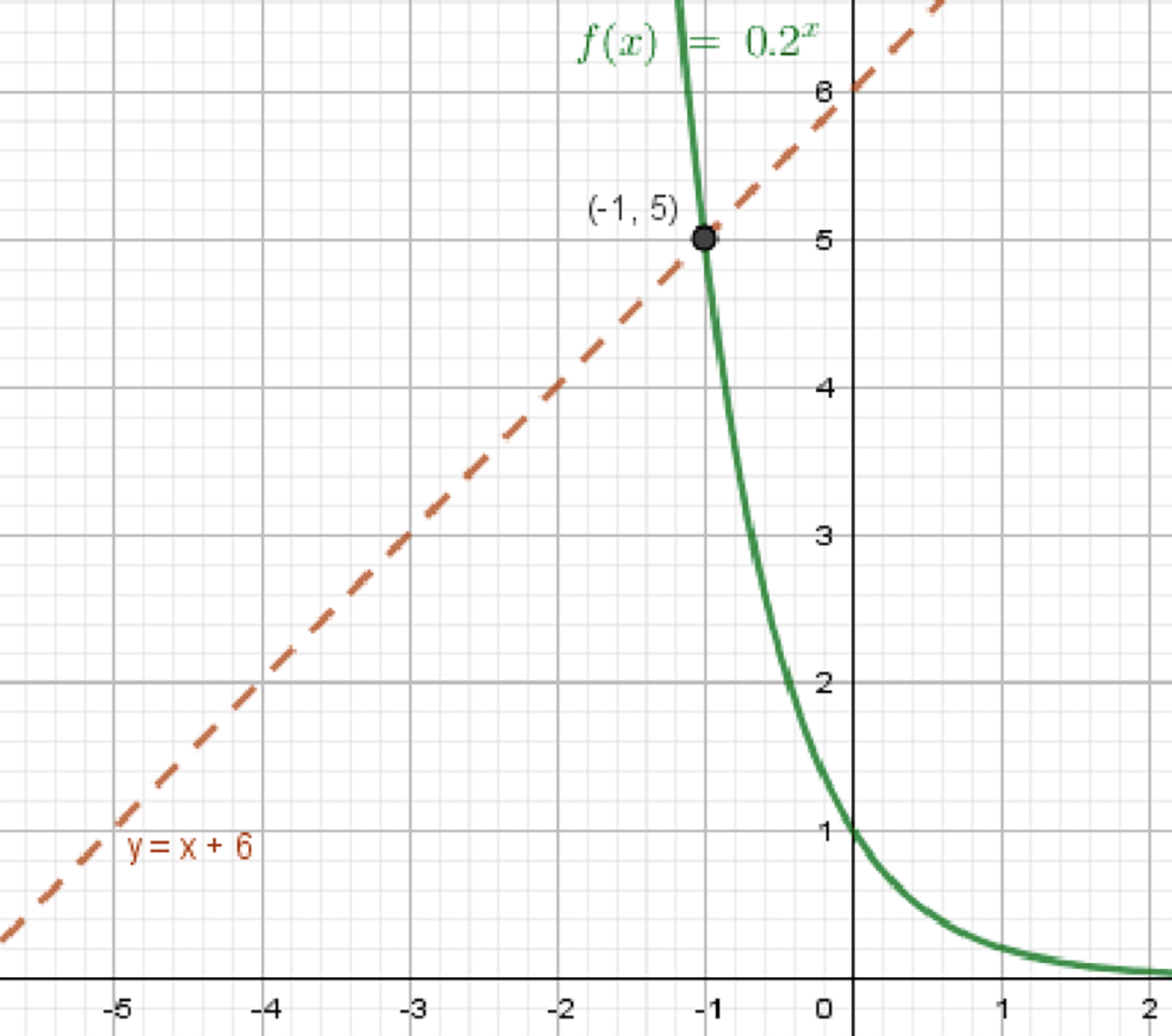
г) 0 , 2 x = x + 6 0,2^x = x + 6 y = 0 , 2 x y = 0,2^x
x − 2 − 1 0 y 25 5 1 \begin{array}{|c|c|c|c|} \hline x & -2 & -1 & 0 \\ \hline y & 25 & 5 & 1 \\ \hline \end{array}
y = x + 6 y = x + 6
x − 6 0 y 0 6 \begin{array}{|c|c|c|} \hline x & -6 & 0 \\ \hline y & 0 & 6 \\ \hline \end{array}
Графики функций:
Ответ: x = − 1 x = -1
Подробный ответ:
а) Решить уравнение:
2 x = − 2 x + 8 2^x = -2x + 8
Шаг 1: Распишем уравнение как равенство двух функций
Мы хотим найти x x двух функций равны:
y 1 = 2 x y_1 = 2^x показательная функция y 2 = − 2 x + 8 y_2 = -2x + 8 линейная функция (прямая) Шаг 2: Построим таблицу значений для y 1 = 2 x y_1 = 2^x
Функция 2 x 2^x x x
x y = 2 x 0 1 1 2 2 4 3 8 4 16 \begin{array}{|c|c|} \hline x & y = 2^x \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ 3 & 8 \\ 4 & 16 \\ \hline \end{array}
Комментарий: при x = 0 x = 0 2 x = 1 2^x = 1 x x 2 , 4 , 8 , 16 2, 4, 8, 16
Шаг 3: Построим таблицу значений для y 2 = − 2 x + 8 y_2 = -2x + 8
Это линейная функция, убывающая с угловым коэффициентом − 2 -2
x y = − 2 x + 8 0 8 1 6 2 4 3 2 4 0 \begin{array}{|c|c|} \hline x & y = -2x + 8 \\ \hline 0 & 8 \\ 1 & 6 \\ 2 & 4 \\ 3 & 2 \\ 4 & 0 \\ \hline \end{array}
Комментарий: при x = 0 x = 0 y = 8 y = 8 x x y y
Шаг 4: Сравним значения обеих функций
Поищем, при каком x x
x x y = 2 x y = 2^x y = − 2 x + 8 y = -2x + 8 0 1 8 1 2 6 2 4 4 3 8 2
При x = 2 x = 2 4 . Это точка пересечения графиков, то есть решение уравнения.
Ответ:
x = 2 \boxed{x = 2}
б) Решить уравнение:
( 1 3 ) x = x + 11 \left(\frac{1}{3}\right)^x = x + 11
Шаг 1: Представим как две функции
y 1 = ( 1 3 ) x y_1 = \left(\frac{1}{3}\right)^x убывающая показательная функция y 2 = x + 11 y_2 = x + 11 возрастающая прямая Шаг 2: Таблица значений для y = ( 1 3 ) x y = \left(\frac{1}{3}\right)^x
Эта функция убывает, потому что основание дробное ( 1 3 < 1 ) \left( \frac{1}{3} < 1 \right)
x y = ( 1 3 ) x − 2 9 ( = 3 2 ) − 1 3 0 1 1 1 3 2 1 9 \begin{array}{|c|c|} \hline x & y = \left(\frac{1}{3}\right)^x \\ \hline -2 & 9 \quad \left(= 3^2\right) \\ -1 & 3 \\ 0 & 1 \\ 1 & \frac{1}{3} \\ 2 & \frac{1}{9} \\ \hline \end{array}
Шаг 3: Таблица значений для y = x + 11 y = x + 11
Это прямая, растущая с коэффициентом 1:
x y = x + 11 − 4 7 − 2 9 0 11 1 12 \begin{array}{|c|c|} \hline x & y = x + 11 \\ \hline -4 & 7 \\ -2 & 9 \\ 0 & 11 \\ 1 & 12 \\ \hline \end{array}
Шаг 4: Сравнение значений
x x y = ( 1 3 ) x y = \left(\frac{1}{3}\right)^x y = x + 11 y = x + 11 -2 9 9 -1 3 10 0 1 11
При x = − 2 x = -2 9 , это точка пересечения.
Ответ:
x = − 2 \boxed{x = -2}
в) Решить уравнение:
3 x = − x + 1 3^x = -x + 1
Шаг 1: Представим как две функции
y 1 = 3 x y_1 = 3^x возрастающая экспонента y 2 = − x + 1 y_2 = -x + 1 убывающая прямая Шаг 2: Таблица значений y = 3 x y = 3^x
x y = 3 x 0 1 1 3 2 9 \begin{array}{|c|c|} \hline x & y = 3^x \\ \hline 0 & 1 \\ 1 & 3 \\ 2 & 9 \\ \hline \end{array}
Шаг 3: Таблица значений y = − x + 1 y = -x + 1
x y = − x + 1 − 2 3 0 1 1 0 \begin{array}{|c|c|} \hline x & y = -x + 1 \\ \hline -2 & 3 \\ 0 & 1 \\ 1 & 0 \\ \hline \end{array}
Шаг 4: Сравнение значений
x x y = 3 x y = 3^x y = − x + 1 y = -x + 1 0 1 1 1 3 0
Оба графика пересекаются в точке x = 0 x = 0
Ответ:
x = 0 \boxed{x = 0}
г) Решить уравнение:
0,2 x = x + 6 0{,}2^x = x + 6
Шаг 1: Представим как функции
y 1 = 0,2 x y_1 = 0{,}2^x убывающая показательная функция (основание 0,2 < 1 0{,}2 < 1 y 2 = x + 6 y_2 = x + 6 прямая Шаг 2: Таблица значений y = 0,2 x y = 0{,}2^x
x y = 0,2 x − 2 25 ( = 1 0,2 2 = 1 0,04 ) − 1 5 0 1 1 0,2 \begin{array}{|c|c|} \hline x & y = 0{,}2^x \\ \hline -2 & 25 \quad \left(= \frac{1}{0{,}2^2} = \frac{1}{0{,}04}\right) \\ -1 & 5 \\ 0 & 1 \\ 1 & 0{,}2 \\ \hline \end{array}
Шаг 3: Таблица значений y = x + 6 y = x + 6
x y = x + 6 − 6 0 − 2 4 − 1 5 0 6 \begin{array}{|c|c|} \hline x & y = x + 6 \\ \hline -6 & 0 \\ -2 & 4 \\ -1 & 5 \\ 0 & 6 \\ \hline \end{array}
Шаг 4: Сравнение значений
x x y = 0,2 x y = 0{,}2^x y = x + 6 y = x + 6 -1 5 5 0 1 6
При x = − 1 x = -1 5 — это и есть решение.
Ответ:
x = − 1