Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 39.42 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) , ;
б) , ;
в) , ;
г) ,
При каких значениях график заданной показательной функции лежит выше графика заданной линейной функции:
а) , ;
Функция возрастает на ;
Функция убывает на ;
Методом перебора найдем пересечение:
;
;
Ответ: .
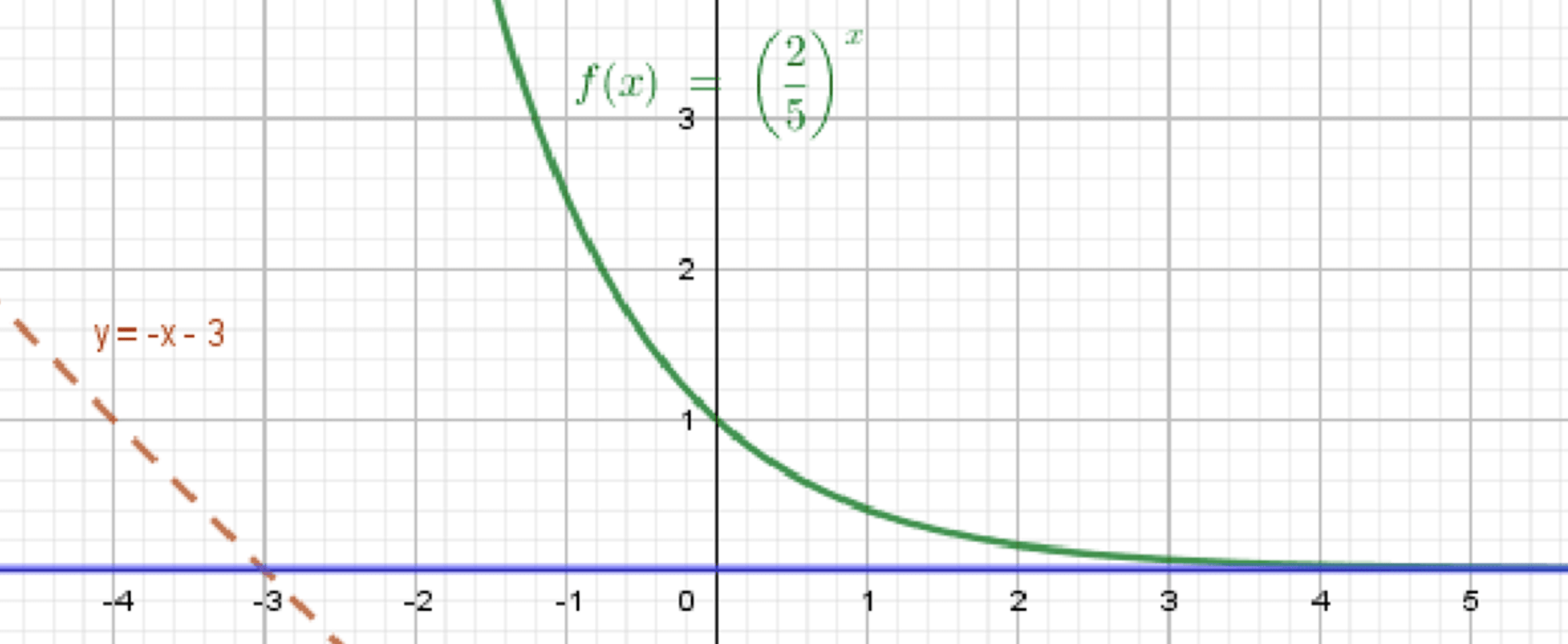
б) , ;
— показательная функция:
— уравнение прямой:
Графики функций:
Ответ: .
в) , ;
Функция возрастает на ;
Функция убывает на ;
Методом перебора найдем пересечение:
;
;
Ответ: .
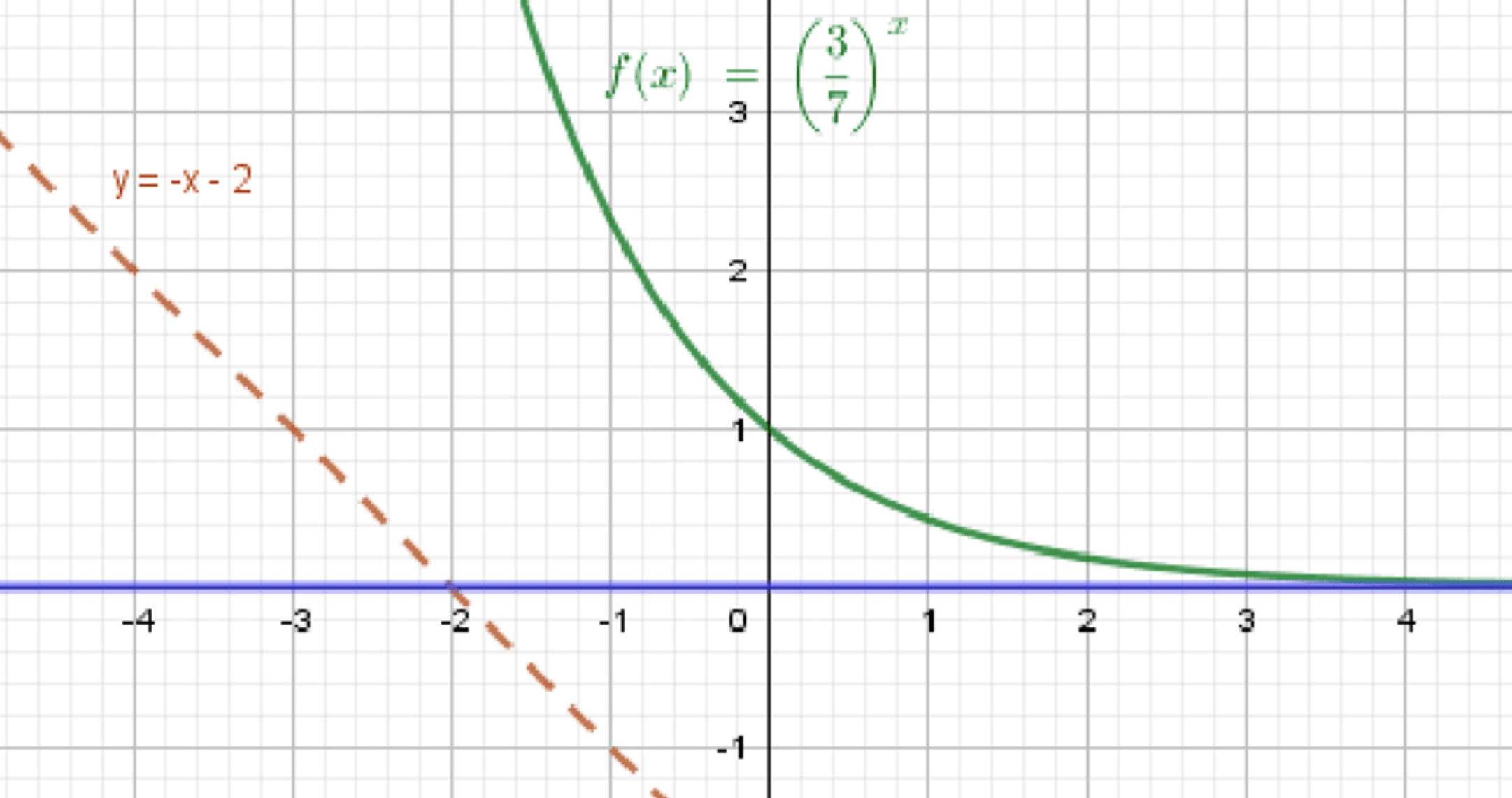
г) , ;
— показательная функция:
— уравнение прямой:
Графики функций:
Ответ: .
При каких значениях график заданной показательной функции лежит выше графика заданной линейной функции?
То есть:
Найти множество таких , при которых
где:
- — показательная функция
- — линейная функция
а) ,
1. Поведение функций
- :
Это показательная функция с основанием .
Значит, она возрастает на всей числовой прямой , то есть чем больше , тем больше значение функции. - :
Это линейная функция с коэффициентом при равным .
Значит, функция убывает на всей числовой прямой.
2. Найдём точку пересечения графиков
Для этого приравняем правые части уравнений:
Это уравнение не решается аналитически в общем виде, но можно найти точку пересечения методом подбора (или графически).
Проверим :
Значения равны — это точка пересечения графиков.
3. Анализ взаимного расположения графиков
Так как:
- возрастает
- убывает
- В точке они равны
Следовательно:
- При :
- При :
Ответ:
б) ,
1. Поведение функций
- :
Показательная функция с основанием .
Значит, функция убывает на всей числовой прямой.
График расположен выше оси (всегда ). - :
Линейная функция с угловым коэффициентом — убывает.
Значения могут быть как положительными, так и отрицательными.
2. Таблица значений
Для показательной функции:
Для линейной функции:
3. Анализ
- При :
, → - При :
, → - При :
, → - При больших значениях :
- Показательная функция стремится к
- Линейная функция уходит в
→ Показательная всё равно выше
Вывод:
График показательной функции лежит выше линейной при всех значениях .
Ответ:
в) ,
1. Поведение функций
- :
Это показательная функция с основанием , значит возрастает. - :
Линейная функция с коэффициентом при равным , значит убывает.
2. Найдём точку пересечения
Приравниваем:
Решим подбором:
- :
,
—> Это точка пересечения.
3. Сравнение
- При :
- растёт
- убывает
→
- При :
Ответ:
г) ,
1. Поведение функций
- :
Основание → функция убывает, значения всегда положительные. - :
Линейная функция, убывает (коэффициент )
2. Таблица значений
Для показательной:
Для линейной:
3. Анализ
- При всех проверенных значениях:
- Показательная стремится к справа и слева
- Линейная стремится к при , и к при ,
но значительно медленнее возрастает/убывает
→ График показательной функции всегда выше
Ответ:
Итоговые ответы:
а)
б)
в)
г)