ГДЗ 10-11 Класс Номер 39.44 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Решите уравнение:

а) $2^x — 1 = \sqrt{x}$;

б) $\left(\frac{1}{4}\right)^x = \sqrt{x} + 1$;

в) $3^x — 1 = -\sqrt{x}$;

г) $\left(\frac{1}{3}\right)^x = \sqrt{x} + 1$

Решить уравнение:

а) $2^x — 1 = \sqrt{x}$;

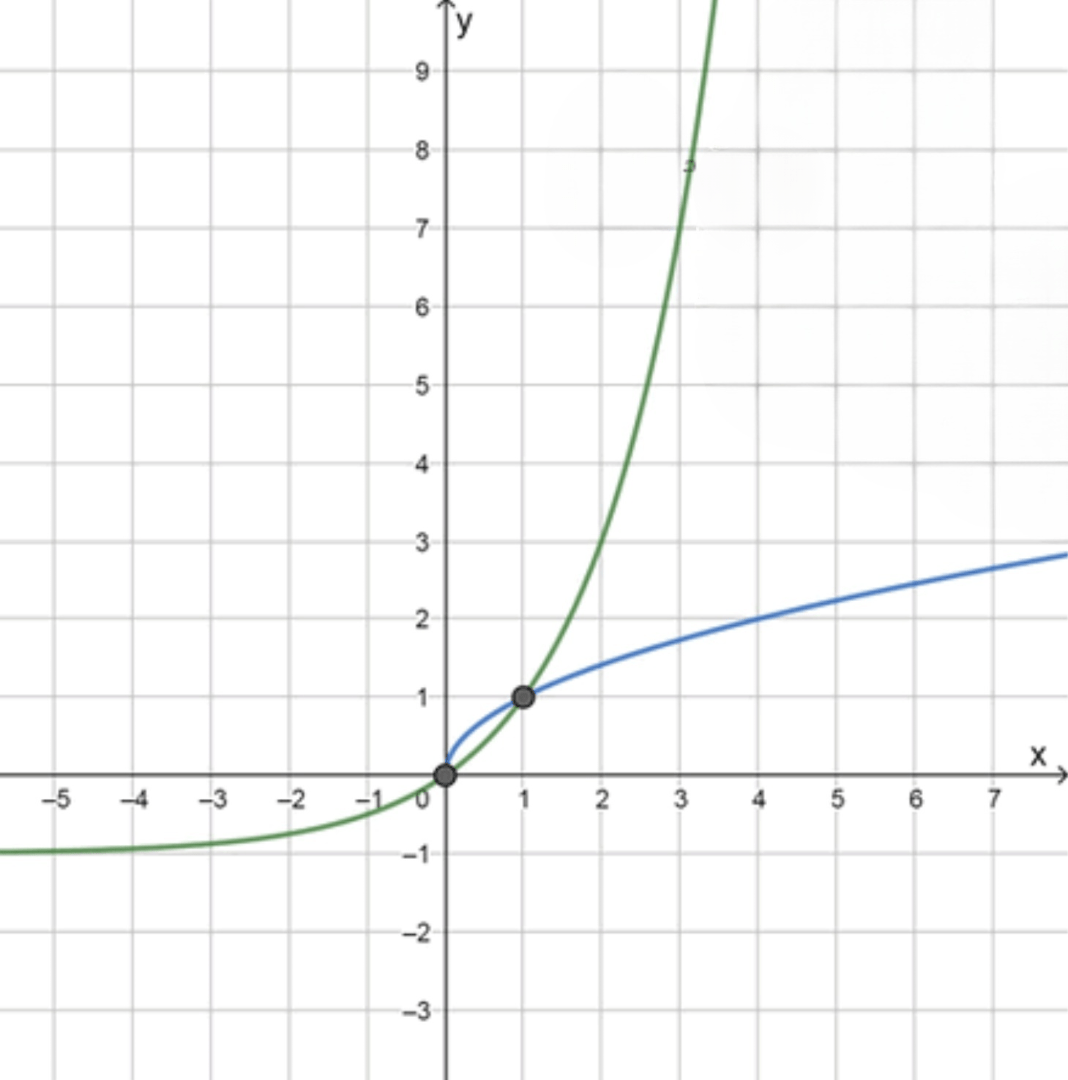
$y = 2^x — 1$ — показательная функция:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 0 & 1 & 3 \\ \hline \end{array}$$

$y = \sqrt{x}$ — уравнение ветви параболы:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 4 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

Графики функций:

Ответ: 0; 1.

б) $\left(\frac{1}{4}\right)^x = \sqrt{x} + 1$;

Выражение имеет смысл при $x \geq 0$;

Функция $y = \left(\frac{1}{4}\right)^x$ убывает на $[0; +\infty)$;

Функция $y = \sqrt{x} + 1$ возрастает на $[0; +\infty)$;

Методом перебора найдем пересечение:

$y_1(0) = \left(\frac{1}{4}\right)^0 = 1$;
$y_2(0) = \sqrt{0} + 1 = 1$;

Ответ: 0.

в) $3^x — 1 = -\sqrt{x}$;

Выражение имеет смысл при $x \geq 0$;

Функция $y = 3^x — 1$ возрастает на $[0; +\infty)$;
Функция $y = -\sqrt{x}$ убывает на $[0; +\infty)$;

Методом перебора найдем пересечение:
$y_1(0) = 3^0 — 1 = 1 — 1 = 0$;
$y_2(0) = -\sqrt{0} = 0$;

Ответ: 0.

г) $\left(\frac{1}{3}\right)^x = \sqrt{x} + 1$;

Выражение имеет смысл при $x \geq 0$;

Функция $y = \left(\frac{1}{3}\right)^x$ убывает на $[0; +\infty)$;
Функция $y = \sqrt{x} + 1$ возрастает на $[0; +\infty)$;

Методом перебора найдем пересечение:
$y_1(0) = \left(\frac{1}{3}\right)^0 = 1$;
$y_2(0) = \sqrt{0} + 1 = 1$;

Ответ: 0.

а) $2^x — 1 = \sqrt{x}$

1. Область определения (ОДЗ):

Правая часть содержит корень $\sqrt{x}$, который определён при $x \geq 0$. Левая часть $2^x — 1$ определена при всех $x \in \mathbb{R}$.

Следовательно, ОДЗ:

$$x \geq 0$$

2. Анализ функций

Левая часть: $y_1 = 2^x — 1$
Это показательная функция с основанием $2 > 1$, сдвинутая вниз на 1.
Функция возрастает на всей области определения и принимает значения $y > -1$.

Правая часть: $y_2 = \sqrt{x}$
Корневая функция. Определена при $x \geq 0$, возрастает. Значения $y \geq 0$.

3. Таблицы значений

Для $y_1 = 2^x — 1$:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 0 & 1 & 3 \\ \hline \end{array}$$

Для $y_2 = \sqrt{x}$:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 4 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

4. Подстановка значений

• При $x = 0$:
  $2^0 — 1 = 1 — 1 = 0$,
  $\sqrt{0} = 0$,
  уравнение выполняется.
• При $x = 1$:
  $2^1 — 1 = 1$,
  $\sqrt{1} = 1$,
  уравнение выполняется.
• При $x = 2$:
  $2^2 — 1 = 3$,
  $\sqrt{2} \approx 1.41$,
  значения не равны.
• При $x = 4$:
  $2^4 — 1 = 15$,
  $\sqrt{4} = 2$,
  значения не равны.

Ответ:

$$x=0;x=1$$

б) $\left(\dfrac{1}{4}\right)^x = \sqrt{x} + 1$

1. Область определения:

Правая часть определена при $x \geq 0$. Левая часть определена при всех $x \in \mathbb{R}$.

ОДЗ:

$$x \geq 0$$

2. Анализ функций

• $y_1 = \left(\dfrac{1}{4}\right)^x$: убывающая показательная функция, значения положительные.
• $y_2 = \sqrt{x} + 1$: возрастающая корневая функция, значения от 1 и выше.

3. Подстановка значений

• $x = 0$:
  $y_1 = 1$,
  $y_2 = 0 + 1 = 1$ — уравнение выполняется.
• $x = 1$:
  $y_1 = \dfrac{1}{4}$,
  $y_2 = 1 + 1 = 2$ — не выполняется.
• $x = 2$:
  $y_1 \approx 0.0625$,
  $y_2 \approx 1.41 + 1 = 2.41$

Совпадение только при $x = 0$.

Ответ:

$$x = 0$$

в) $3^x — 1 = -\sqrt{x}$

1. Область определения:

Корень в правой части требует $x \geq 0$. Левая часть определена всюду.

ОДЗ:

$$x \geq 0$$

2. Анализ функций

• $y_1 = 3^x — 1$: возрастает, значения от 0 и выше.
• $y_2 = -\sqrt{x}$: убывает, значения от 0 и ниже.

3. Подстановка значений

• $x = 0$:
  $y_1 = 1 — 1 = 0$,
  $y_2 = -\sqrt{0} = 0$,
  уравнение выполняется.
• $x = 1$:
  $y_1 = 3 — 1 = 2$,
  $y_2 = -1$ — не выполняется.

Совпадение только при $x = 0$.

Ответ:

$$x = 0$$

г) $\left(\dfrac{1}{3}\right)^x = \sqrt{x} + 1$

1. Область определения:

Корень требует $x \geq 0$

ОДЗ:

$$x \geq 0$$

2. Анализ функций

• $y_1 = \left(\dfrac{1}{3}\right)^x$: убывает, значения положительные.
• $y_2 = \sqrt{x} + 1$: возрастает, значения от 1 и выше.

3. Подстановка значений

• $x = 0$:
  $y_1 = 1$,
  $y_2 = 0 + 1 = 1$,
  уравнение выполняется.
• $x = 1$:
  $y_1 \approx 0.33$,
  $y_2 = 2$ — не выполняется.

Совпадение только при $x = 0$.

Ответ:

$$x = 0$$

Итоговые ответы:

а) $x = 0; 1$
б) $x = 0$
в) $x = 0$
г) $x=0$