ГДЗ 10-11 Класс Номер 4.11 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Найдите на числовой окружности точку, которая соответствует заданному числу:

а) $\frac{25\pi }{4}$

б) $-\frac{26\pi }{3}$

в) $-\frac{25\pi }{6}$

г) $\frac{16\pi }{3}$

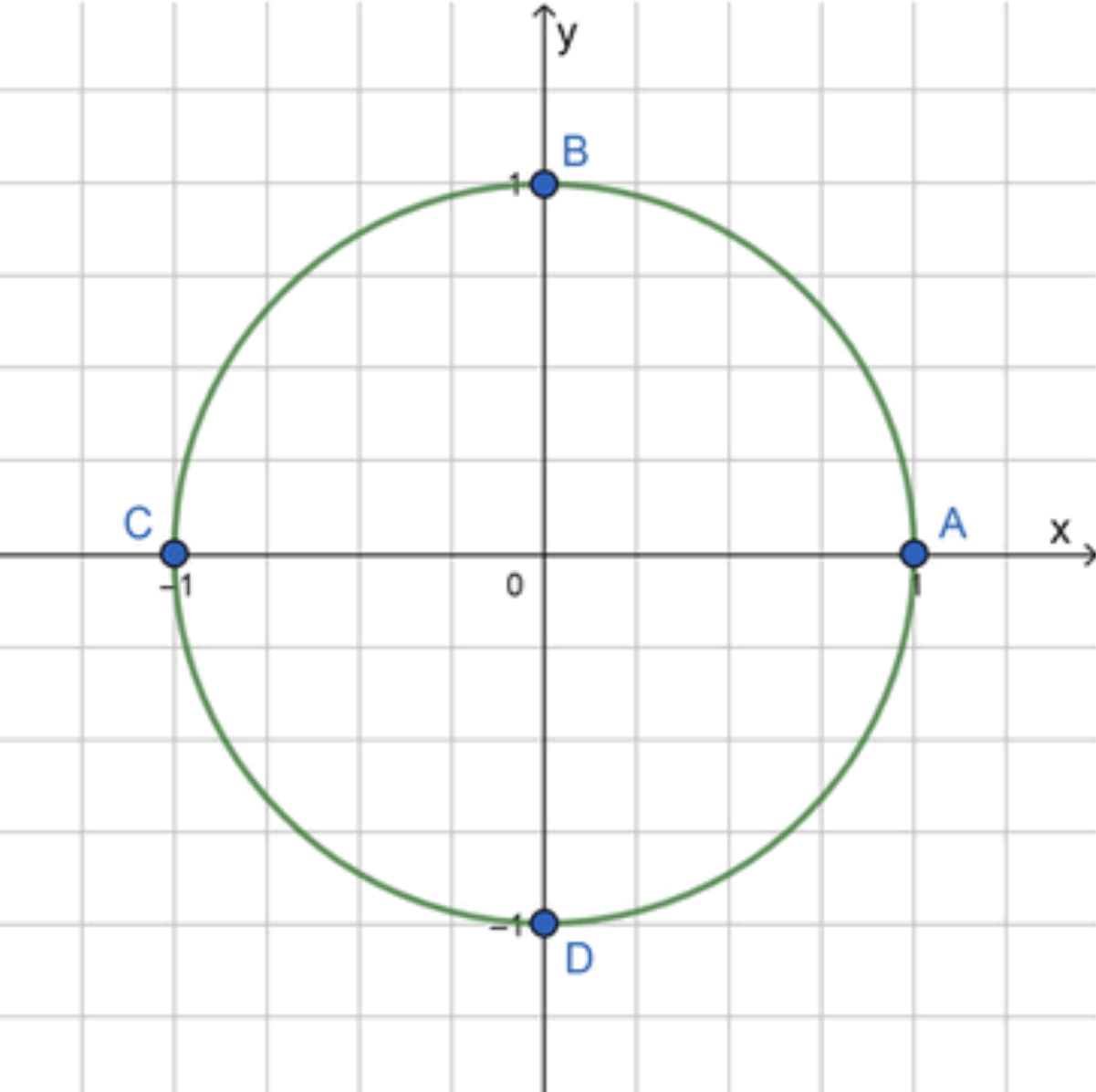
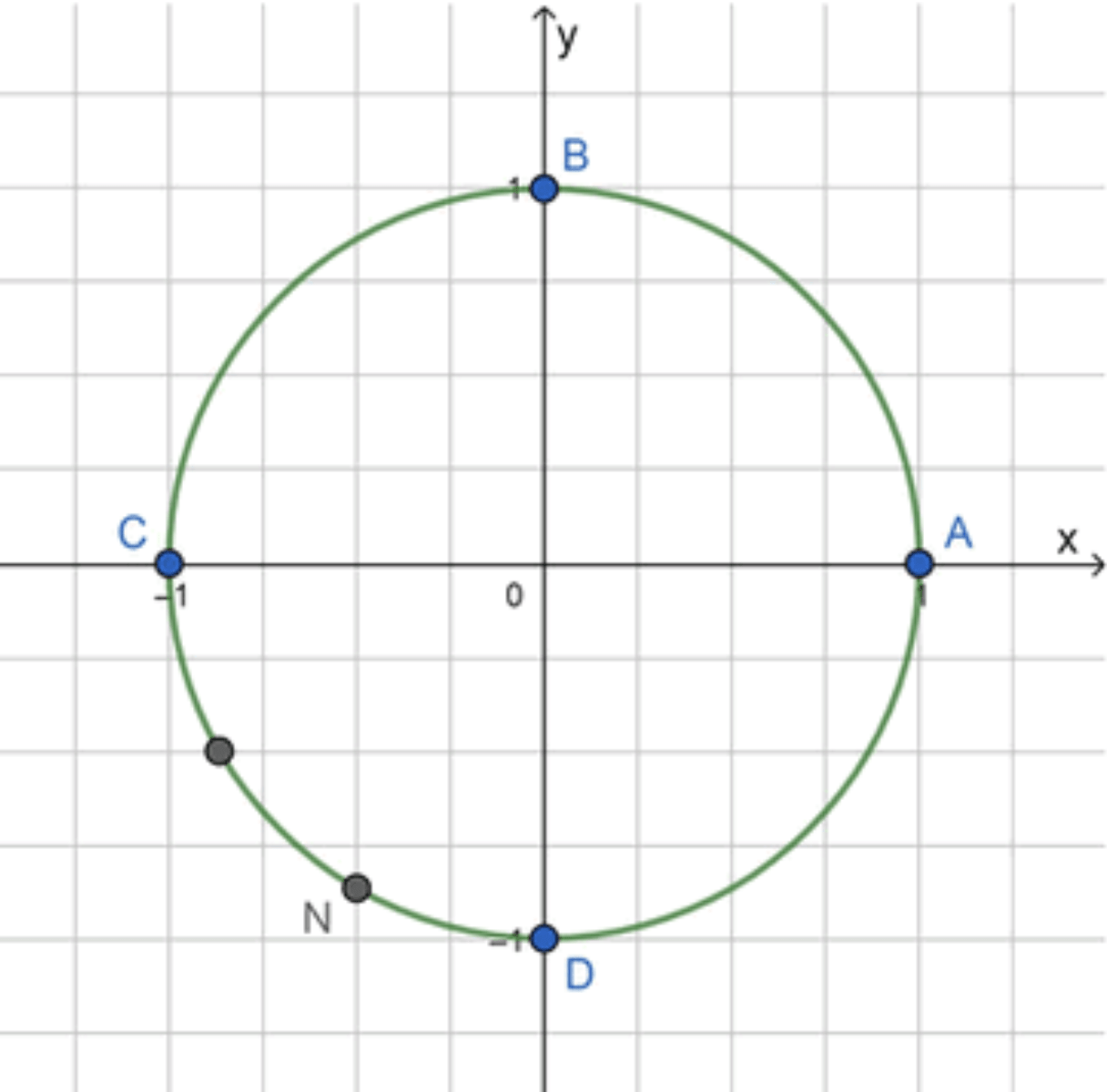
Изобразим окружность с основными точками:

а) $\frac{25\pi}{4} = \frac{25\pi}{4} — 6\pi = \frac{\pi}{4}$;
Разделим $AB$ на две равные части:

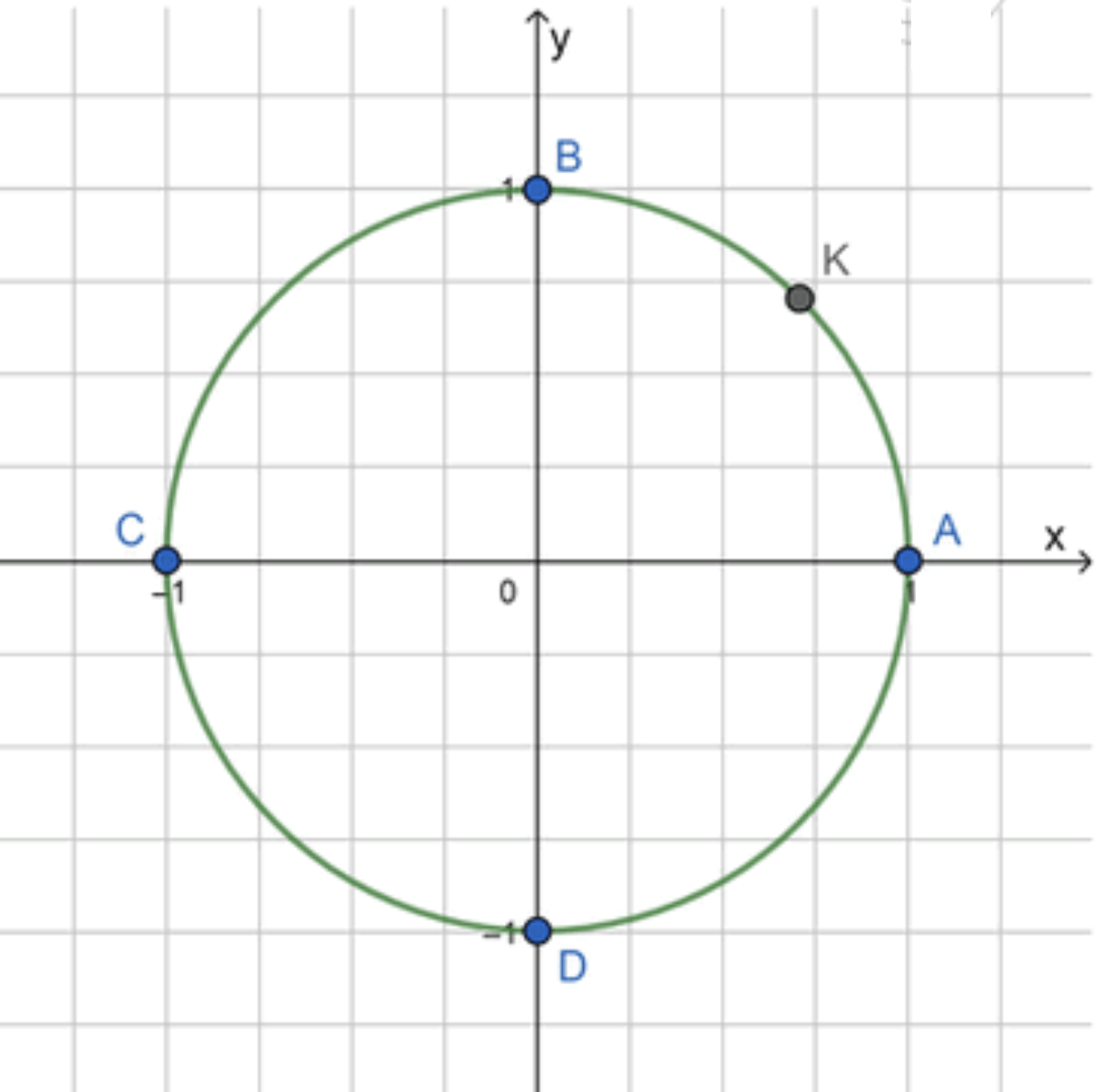
$$AK = \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4};$$

Ответ: $K = K\left(\frac{25\pi}{4}\right)$.

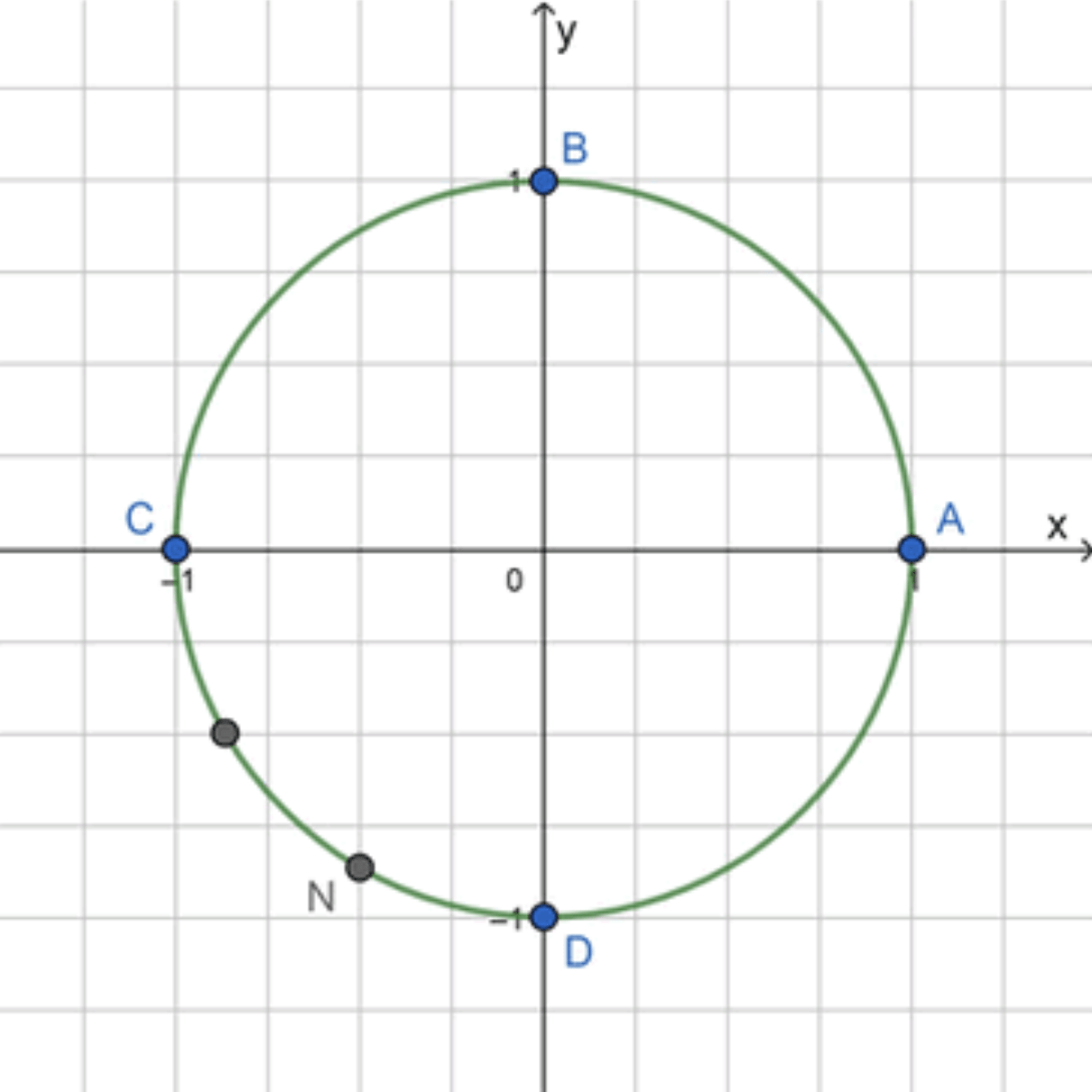
б) $-\frac{26\pi}{3} = 10\pi — \frac{26\pi}{3} = \frac{4\pi}{3} = \pi + \frac{\pi}{3}$;
Разделим $CD$ на три равных части:

$$AN = AC + CN = \pi + \frac{2}{3} \cdot \frac{\pi}{2} = \pi + \frac{\pi}{3} = \frac{4\pi}{3};$$

Ответ: $N = N\left(-\frac{26\pi}{3}\right)$.

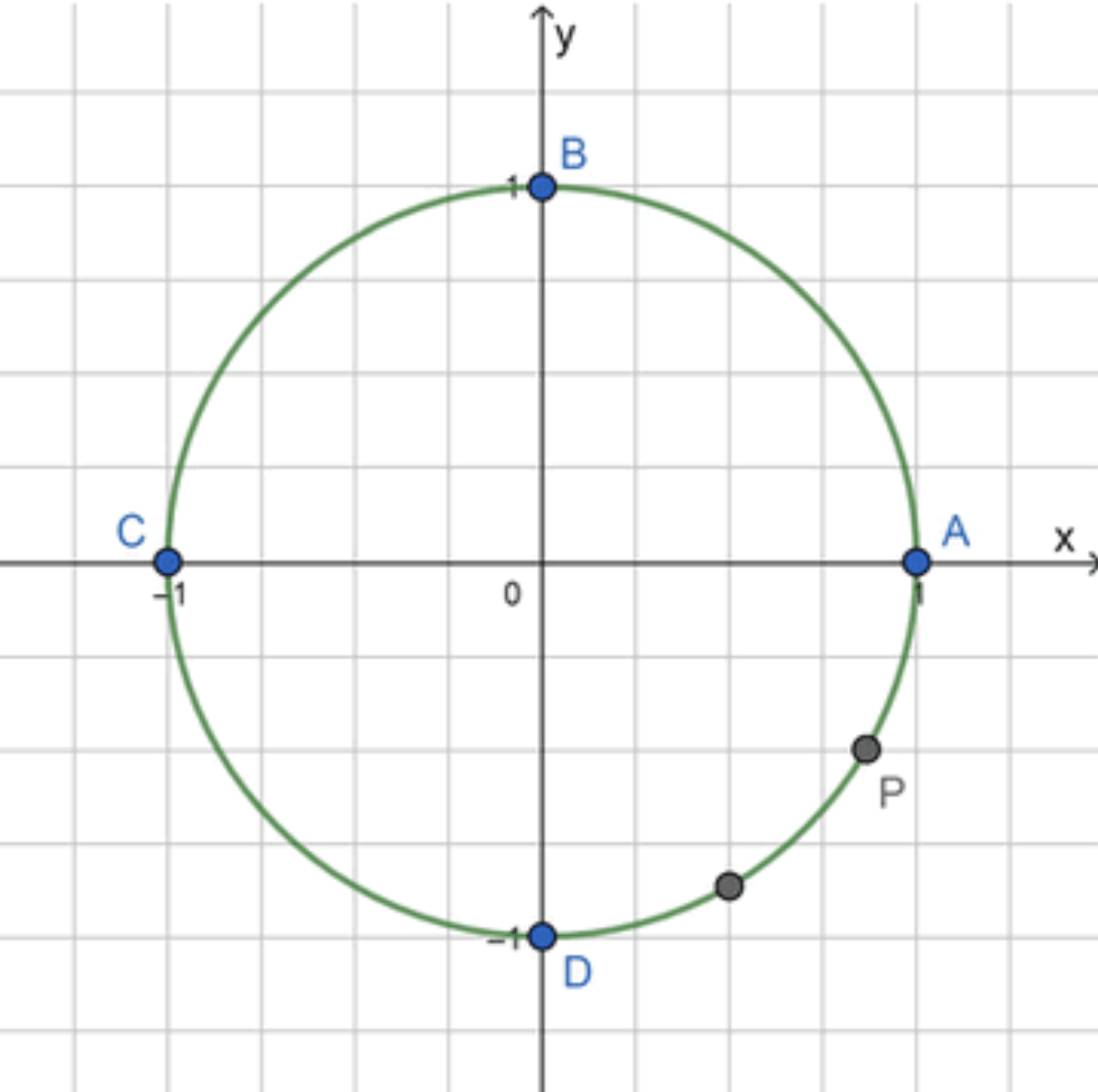
в) $-\frac{25\pi}{6} = 6\pi — \frac{25\pi}{6} = \frac{11\pi}{6} = \frac{3\pi}{2} + \frac{\pi}{3}$;
Разделим $DA$ на три равных части:

$$AP = AD + DP = \frac{3\pi}{2} + \frac{2}{3} \cdot \frac{\pi}{2} = \frac{3\pi}{2} + \frac{\pi}{3} = \frac{11\pi}{6};$$

Ответ: $P = P\left(-\frac{25\pi}{6}\right)$.

г) $\frac{16\pi}{3} = \frac{16\pi}{3} — 4\pi = \frac{4\pi}{3} = \pi + \frac{\pi}{3}$;
Разделим $CD$ на три равных части:

$$AN = AC + CN = \pi + \frac{2}{3} \cdot \frac{\pi}{2} = \pi + \frac{\pi}{3} = \frac{4\pi}{3};$$

Ответ: $N = N\left(\frac{16\pi}{3}\right)$.

а) $\frac{25\pi}{4}$

Шаг 1. Приводим к углу от 0 до $2\pi$

$$\frac{25\pi}{4} = 6\pi + \frac{\pi}{4} \Rightarrow \text{вычтем } 6\pi = \frac{24\pi}{4}:$$ $$\frac{25\pi}{4} — \frac{24\pi}{4} = \frac{\pi}{4}$$

Шаг 2. Определим, где находится $\frac{\pi}{4}$

• Угол $\frac{\pi}{4}$ находится в первой четверти, между $0$ и $\frac{\pi}{2}$, то есть между точками $A$ и $B$.
• $AB = \frac{\pi}{2}$

Шаг 3. Разделим дугу $AB$ на 2 части

$$AK = \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4}$$

Шаг 4. Ответ:

$$K = K\left(\frac{25\pi}{4}\right)$$

б) $-\frac{26\pi}{3}$

Шаг 1. Преобразуем в положительный угол

• Отрицательный угол, нужно привести его к положительному значению:

$$— \frac{26\pi}{3} = 10\pi — \frac{26\pi}{3} = \frac{30\pi}{3} — \frac{26\pi}{3} = \frac{4\pi}{3}$$

Шаг 2. Разложим угол:

$$\frac{4\pi}{3} = \pi + \frac{\pi}{3}$$

• Значит, точка лежит в третьей четверти, после точки $C$ (угол $\pi$).

Шаг 3. Дуга $CD = \frac{\pi}{2}$

Разделим её на 3 части:

$$\text{Одна часть} = \frac{\pi}{2} : 3 = \frac{\pi}{6}$$

Нам нужно пройти от точки $C$ 2 части:

$$CN = 2 \cdot \frac{\pi}{6} = \frac{\pi}{3}$$

Шаг 4. Сложим:

$$AN = AC + CN = \pi + \frac{\pi}{3} = \frac{4\pi}{3}$$

Шаг 5. Ответ:

$$N = N\left(-\frac{26\pi}{3}\right)$$

в) $-\frac{25\pi}{6}$

Шаг 1. Приведение к положительному углу

$$6\pi = \frac{36\pi}{6}, \quad \Rightarrow \frac{36\pi}{6} — \frac{25\pi}{6} = \frac{11\pi}{6}$$

Шаг 2. Определим, где находится угол $\frac{11\pi}{6}$

• Это угол между $\frac{3\pi}{2} = \frac{9\pi}{6}$ и $2\pi = \frac{12\pi}{6}$
• Значит, это четвёртая четверть, между точками $D$ и $A$

$$\frac{11\pi}{6} = \frac{3\pi}{2} + \frac{\pi}{3}$$

Шаг 3. Дуга $DA = \frac{\pi}{2} = \frac{3\pi}{6}$

Разделим её на 3 части:

$$\text{Одна часть} = \frac{\pi}{6}$$

Чтобы попасть в точку $P$, нужно пройти две части:

$$DP = 2 \cdot \frac{\pi}{6} = \frac{\pi}{3}$$

Шаг 4. Полный путь:

$$AP = AD + DP = \frac{3\pi}{2} + \frac{\pi}{3} = \frac{9\pi}{6} + \frac{2\pi}{6} = \frac{11\pi}{6}$$

Шаг 5. Ответ:

$$P = P\left(-\frac{25\pi}{6}\right)$$

г) $\frac{16\pi}{3}$

Шаг 1. Приведение к $[0, 2\pi)$

$$4\pi = \frac{12\pi}{3}, \quad \frac{16\pi}{3} — \frac{12\pi}{3} = \frac{4\pi}{3}$$

Шаг 2. Аналогично пункту б:

$$\frac{4\pi}{3} = \pi + \frac{\pi}{3} \Rightarrow \text{точка находится после } C \text{ на } \frac{\pi}{3}$$

Шаг 3. Разделим дугу $CD = \frac{\pi}{2}$ на 3 части:

$$\frac{\pi}{6} \Rightarrow CN = 2 \cdot \frac{\pi}{6} = \frac{\pi}{3}$$

Шаг 4. Сложим:

$$AN = \pi + \frac{\pi}{3} = \frac{4\pi}{3}$$

Шаг 5. Ответ:

$$N=N\left(\frac{16\pi }{3}\right)$$