ГДЗ 10-11 Класс Номер 4.5 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Найдите на числовой окружности точку, которая соответствует заданному числу:

а) $\frac{\pi}{2}$;

б) $\pi$;

в) $\frac{3\pi}{2}$;

г) $2\pi$

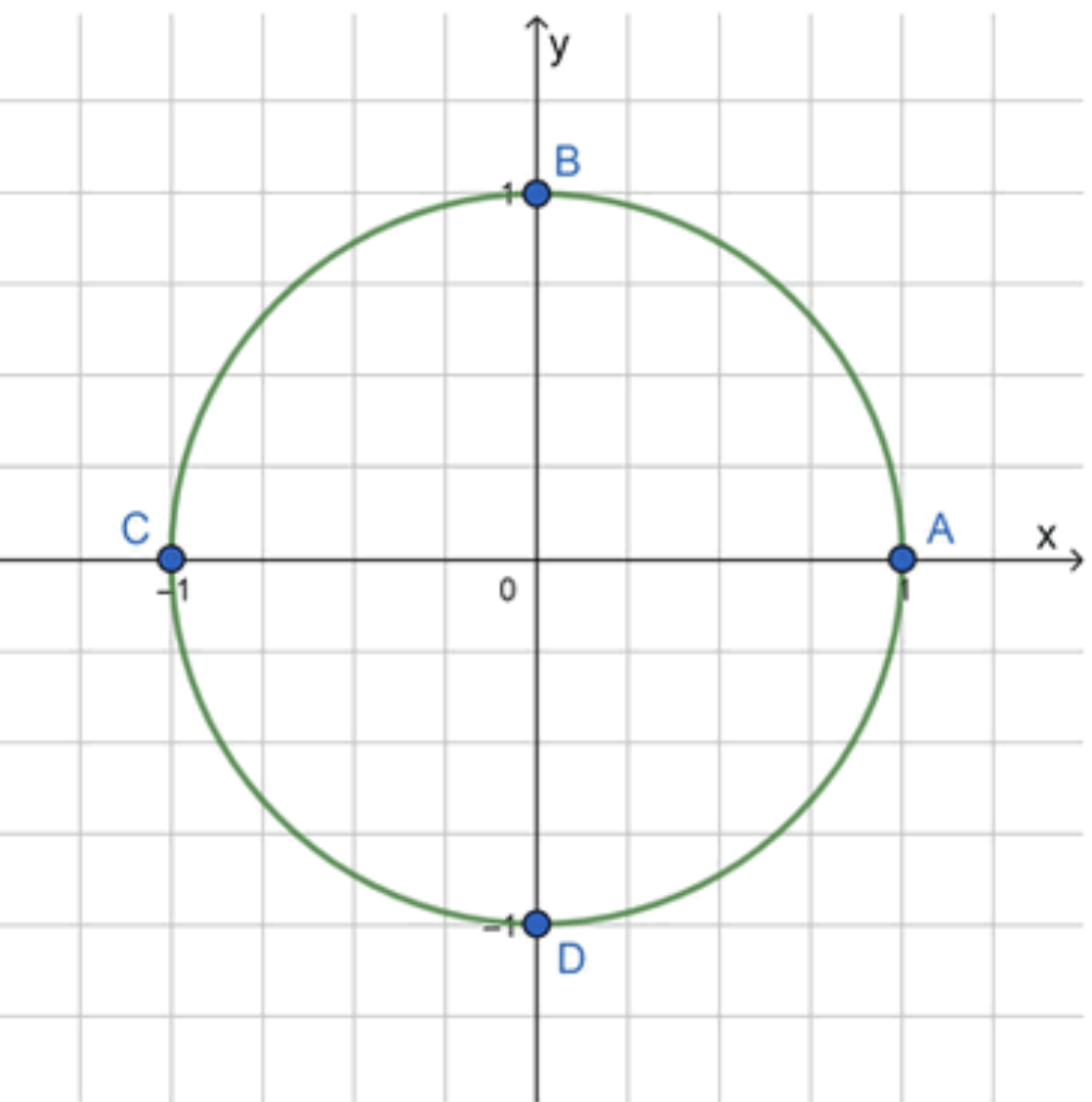
Изобразим окружность с основными точками:

а) $\frac{\pi}{2}$;
Ответ: $B = B\left(\frac{\pi}{2}\right)$.

б) $\pi$;
Ответ: $C = C(\pi)$.

в) $\frac{3\pi}{2}$;
Ответ: $D = D\left(\frac{3\pi}{2}\right)$.

г) $2\pi$;
Ответ: $A = A(2\pi)$.

Окружность и единичная окружность

Предположим, что окружность имеет радиус 1 (единичная окружность). На такой окружности все точки имеют координаты $(\cos(\theta), \sin(\theta))$, где $\theta$ — угол, который образует радиус с положительным направлением оси абсцисс (оси $X$).

Пункт а) $\frac{\pi}{2}$

Для угла $\theta = \frac{\pi}{2}$ мы можем вычислить координаты точки на окружности. Этот угол соответствует четверти окружности, начиная от оси $X$ и двигаясь против часовой стрелки.

• $\cos\left(\frac{\pi}{2}\right) = 0$,
• $\sin\left(\frac{\pi}{2}\right) = 1$.

Таким образом, точка $B$ имеет координаты:

$$B = \left( \cos\left(\frac{\pi}{2}\right), \sin\left(\frac{\pi}{2}\right) \right) = (0, 1).$$

Ответ: $B = B\left(\frac{\pi}{2}\right)$ — точка $B$ на окружности с координатами $(0, 1)$.

Пункт б) $\pi$

Для угла $\theta = \pi$, который соответствует полукруге окружности, мы двигаемся от положительного направления оси $X$ до отрицательного. Это точка, находящаяся на оси $X$, но с отрицательным значением координаты $x$.

• $\cos(\pi) = -1$,
• $\sin(\pi) = 0$.

Таким образом, точка $C$ имеет координаты:

$$C = \left( \cos(\pi), \sin(\pi) \right) = (-1, 0).$$

Ответ: $C = C(\pi)$ — точка $C$ на окружности с координатами $(-1, 0)$.

Пункт в) $\frac{3\pi}{2}$

Для угла $\theta = \frac{3\pi}{2}$ мы находимся в третьей четверти окружности, на оси $Y$, но с отрицательным значением.

• $\cos\left(\frac{3\pi}{2}\right) = 0$,
• $\sin\left(\frac{3\pi}{2}\right) = -1$.

Таким образом, точка $D$ имеет координаты:

$$D = \left( \cos\left(\frac{3\pi}{2}\right), \sin\left(\frac{3\pi}{2}\right) \right) = (0, -1).$$

Ответ: $D = D\left(\frac{3\pi}{2}\right)$ — точка $D$ на окружности с координатами $(0, -1)$.

Пункт г) $2\pi$

Для угла $\theta = 2\pi$ мы возвращаемся на начальную точку, так как угол $2\pi$ соответствует полному обороту по окружности.

• $\cos(2\pi) = 1$,
• $\sin(2\pi) = 0$.

Таким образом, точка $A$ имеет координаты:

$$A = \left( \cos(2\pi), \sin(2\pi) \right) = (1, 0).$$

Ответ: $A = A(2\pi)$ — точка $A$ на окружности с координатами $(1, 0)$.

Итоговые ответы:

а) $B = B\left(\frac{\pi}{2}\right) = (0, 1)$,

б) $C = C(\pi) = (-1, 0)$,

в) $D = D\left(\frac{3\pi}{2}\right) = (0, -1)$,

г) $A = A(2\pi) = (1, 0)$.