ГДЗ 10-11 Класс Номер 4.6 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Найдите на числовой окружности точку, которая соответствует заданному числу:

а) $7\pi$

б) $4\pi$

в) $10\pi$

г) $3\pi$

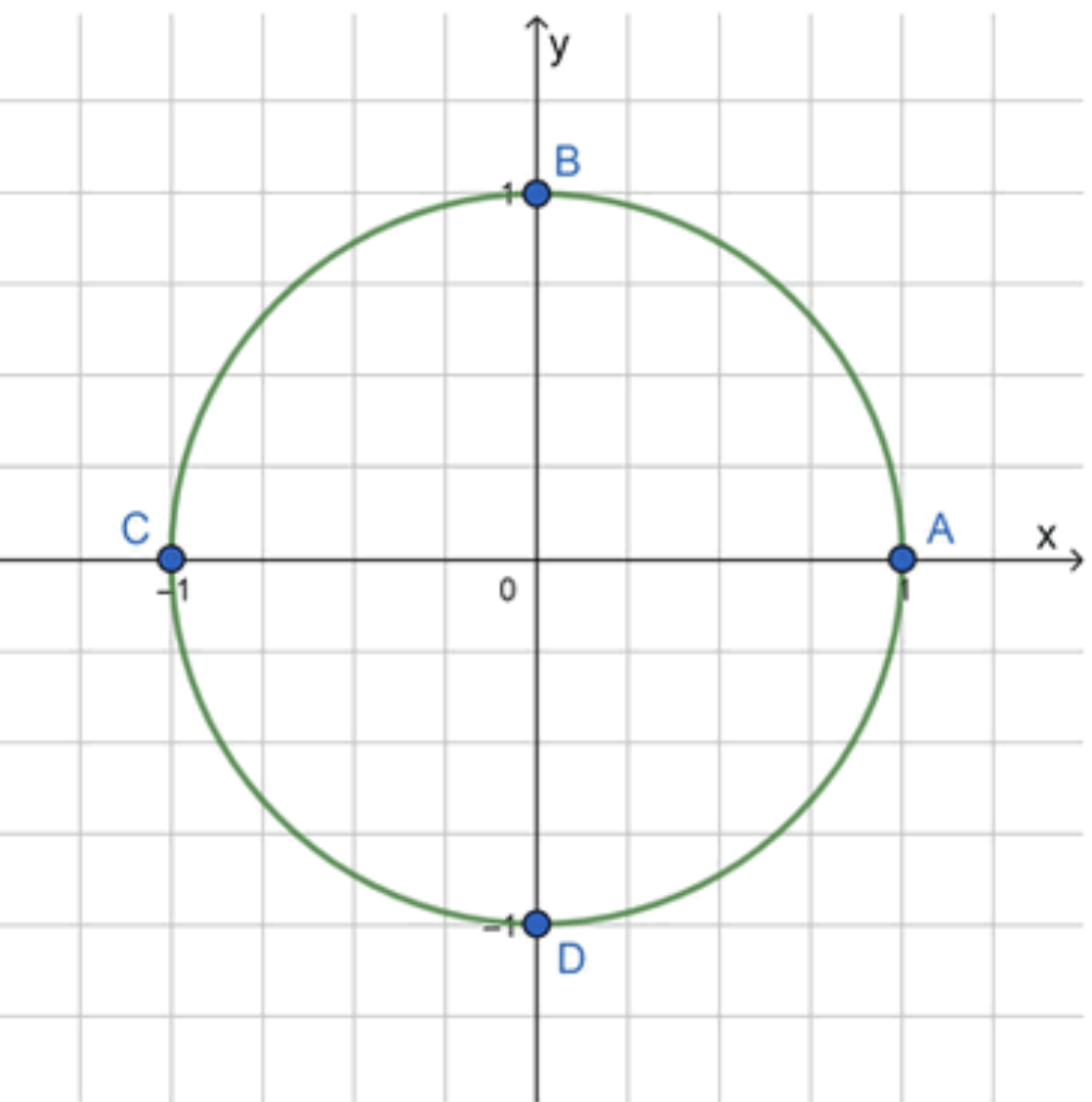
Изобразим окружность с основными точками:

а) $7\pi = 3 \cdot 2\pi + \pi$;
Ответ: $C = C(7\pi)$.

б) $4\pi = 2 \cdot 2\pi + 0$;
Ответ: $A = A(4\pi)$.

в) $10\pi = 5 \cdot 2\pi + 0$;
Ответ: $A = A(10\pi)$.

г) $3\pi = 2\pi + \pi$;
Ответ: $C = C(3\pi)$.

Числовая окружность и её точки

Числовая окружность — это окружность, на которой каждый угол (в радианах) можно представить как точку. Окружность делится на полные круги, каждый из которых равен $2\pi$ радиан.

• Точка на окружности, соответствующая числу $0$, лежит на положительной оси $x$ (это соответствует углу $0$ радиан).
• Точка, соответствующая числу $\pi$, лежит на отрицательной оси $x$.
• Точка, соответствующая числу $2\pi$, снова на положительной оси $x$.
• Точка, соответствующая числу $3\pi$, лежит на отрицательной оси $x$, но сдвинута на угол $\pi$ от точки $2\pi$, и так далее.

Каждое число на окружности можно представить в виде $n \cdot 2\pi + \text{остаток}$, где остаток — это угол, который не является полным кругом. Таким образом, нам нужно использовать понятие остатка от деления числа на $2\pi$, чтобы определить, где находится точка на окружности.

а) $7\pi = 3 \cdot 2\pi + \pi$

Мы видим, что $7\pi$ можно представить как $3 \cdot 2\pi + \pi$. То есть, $7\pi$ — это три полных оборота (каждый по $2\pi$) и ещё дополнительный угол $\pi$.

• Это означает, что на окружности мы сделаем три полных оборота (что не изменит положение) и окажемся на точке, которая соответствует углу $\pi$.
• $\pi$ соответствует точке на числовой окружности, которая расположена на отрицательной оси $x$, то есть в точке $C$.

Ответ: $C = C(7\pi)$.

б) $4\pi = 2 \cdot 2\pi + 0$

Здесь $4\pi$ представлено как $2 \cdot 2\pi + 0$, то есть два полных оборота и никакого дополнительного угла.

• Это означает, что на окружности мы делаем два полных оборота, и остаёмся в той же точке, где начинаем, то есть на положительной оси $x$, которая соответствует числу $0$ радиан.
• Точка, соответствующая числу $0$, это точка $A$.

Ответ: $A = A(4\pi)$.

в) $10\pi = 5 \cdot 2\pi + 0$

Здесь $10\pi$ представлено как $5 \cdot 2\pi + 0$, то есть пять полных оборотов и никакого дополнительного угла.

• Пять полных оборотов также не изменяют положение, и мы остаёмся в той же точке, где начинаем, то есть снова на положительной оси $x$.
• Точка, соответствующая числу $0$, это точка $A$.

Ответ: $A = A(10\pi)$.

г) $3\pi = 2\pi + \pi$

Здесь $3\pi$ представлено как $2\pi + \pi$, то есть два полных оборота и дополнительный угол $\pi$.

• После двух полных оборотов мы окажемся в той же точке, где начинаем (на положительной оси $x$), а затем сделаем ещё поворот на угол $\pi$, что приведёт нас к точке, соответствующей $\pi$, то есть на отрицательной оси $x$.
• Это будет точка $C$.

Ответ: $C = C(3\pi)$.

Итоговые ответы:

а) $C = C(7\pi)$

б) $A = A(4\pi)$

в) $A = A(10\pi)$

г) $C = C(3\pi)$