ГДЗ 10-11 Класс Номер 4.7 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Найдите на числовой окружности точку, которая соответствует заданному числу:

а) $\frac{\pi}{3}$;

б) $\frac{\pi}{4}$;

в) $\frac{\pi}{6}$;

г) $\frac{\pi}{8}$

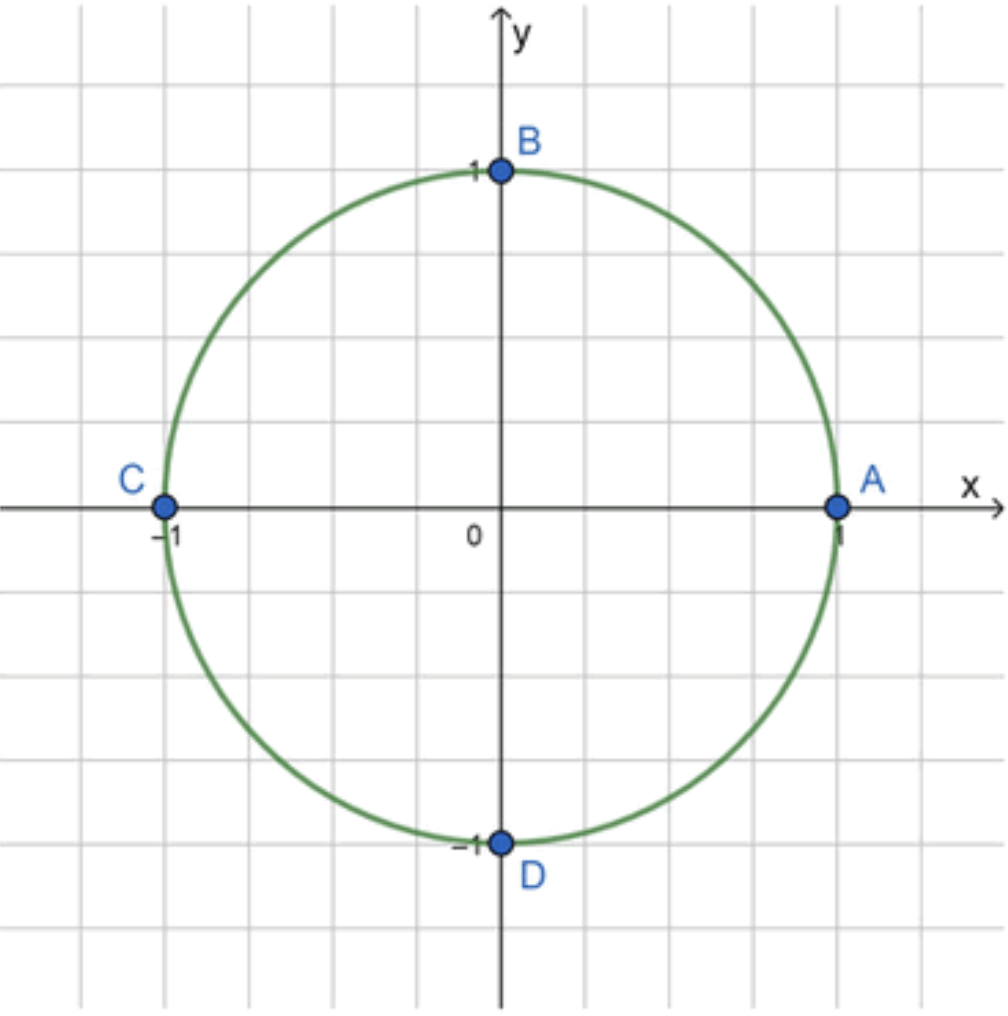
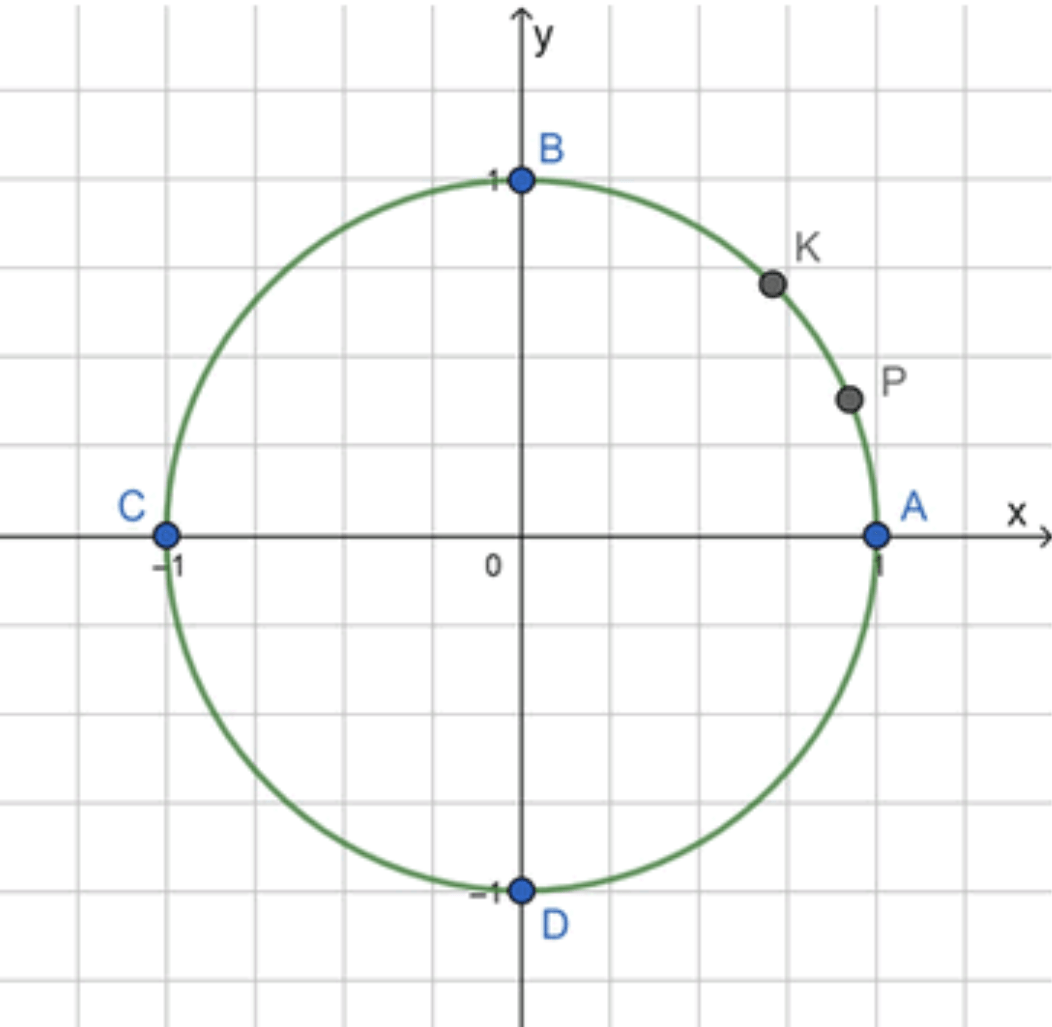
Изобразим окружность с основными точками:

а) $\frac{\pi}{3}$;

Разделим $AB$ на три равные части:

$$AM = \frac{2}{3} \cdot \frac{\pi}{2} = \frac{\pi}{3};$$

Ответ: $M = M\left(\frac{\pi}{3}\right)$.

б) $\frac{\pi}{4}$;

Разделим $AB$ на две равные части:

$$AK = \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4};$$

Ответ: $K = K\left(\frac{\pi}{4}\right)$.

в) $\frac{\pi}{6}$;

Разделим $AB$ на три равные части:

$$AN = \frac{1}{3} \cdot \frac{\pi}{2} = \frac{\pi}{6};$$

Ответ: $N = N\left(\frac{\pi}{6}\right)$.

г) $\frac{\pi}{8}$;

Разделим $AB$ на две равные части:

$$AK = \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4};$$

Разделим $AK$ на две равные части:

$$AP = \frac{1}{2} \cdot \frac{\pi}{4} = \frac{\pi}{8};$$

Ответ: $P = P\left(\frac{\pi}{8}\right)$.

Окружность используется для отложения углов в радианах. Начальная точка — точка $A$, которая соответствует нулевому углу (или $0$ радиан). Дуга от точки $A$ до точки $B$, которая соответствует углу $\frac{\pi}{2}$ (90°), представляет собой одну четверть всей окружности (1/4 круга).

а) $\frac{\pi}{3}$

Шаг 1: Определим дугу $AB$

• Дуга $AB$ соответствует углу $\frac{\pi}{2}$ радиан.
• Это 90 градусов или 1/4 окружности.

Шаг 2: Требуется отложить угол $\frac{\pi}{3}$

• Заметим: $\frac{\pi}{3} < \frac{\pi}{2}$, т.е. точка находится между $A$ и $B$, но ближе к $B$.

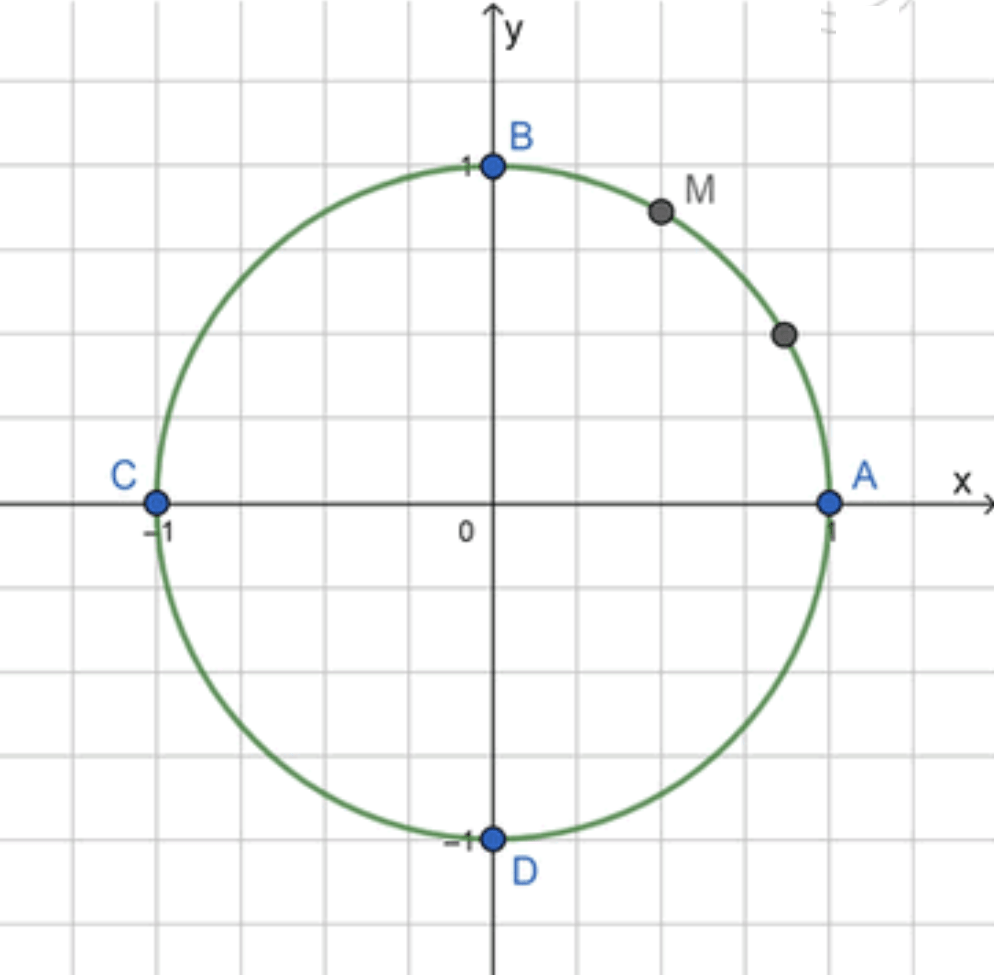
Шаг 3: Разделим дугу $AB$ на 3 равные части

• Длина дуги $AB = \frac{\pi}{2}$.
• Делим её на 3 части:

  $$\text{Одна часть} = \frac{1}{3} \cdot \frac{\pi}{2} = \frac{\pi}{6}.$$

Шаг 4: Чтобы получить $\frac{\pi}{3}$, нужно взять две такие части от точки $A$

$$AM = 2 \cdot \frac{\pi}{6} = \frac{2\pi}{6} = \frac{\pi}{3}.$$

Шаг 5: Отметим точку $M$ на окружности

• Точка $M$ располагается на расстоянии $\frac{\pi}{3}$ по дуге от точки $A$ в направлении против часовой стрелки.

Ответ:

$$M = M\left(\frac{\pi}{3}\right)$$

б) $\frac{\pi}{4}$

Шаг 1: Определим дугу $AB = \frac{\pi}{2}$

Шаг 2: Требуется отложить угол $\frac{\pi}{4}$

• Заметим: $\frac{\pi}{4} = 45^\circ$, половина от $\frac{\pi}{2}$.

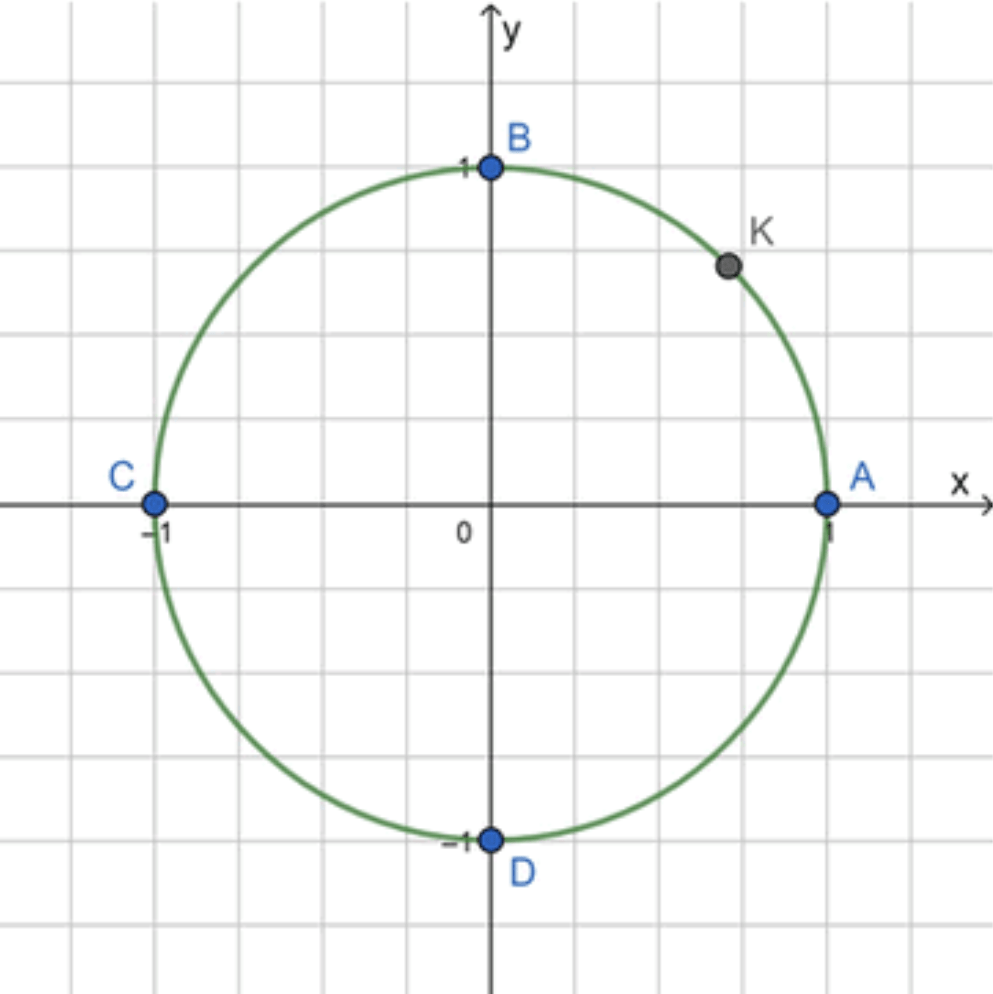
Шаг 3: Разделим дугу $AB$ на 2 равные части

$$AK = \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4}.$$

Шаг 4: Отметим точку $K$ на окружности

• Точка $K$ находится ровно посередине дуги $AB$.

Ответ:

$$K = K\left(\frac{\pi}{4}\right)$$

в) $\frac{\pi}{6}$

Шаг 1: У нас есть дуга $AB = \frac{\pi}{2}$

Шаг 2: Требуется отложить угол $\frac{\pi}{6}$

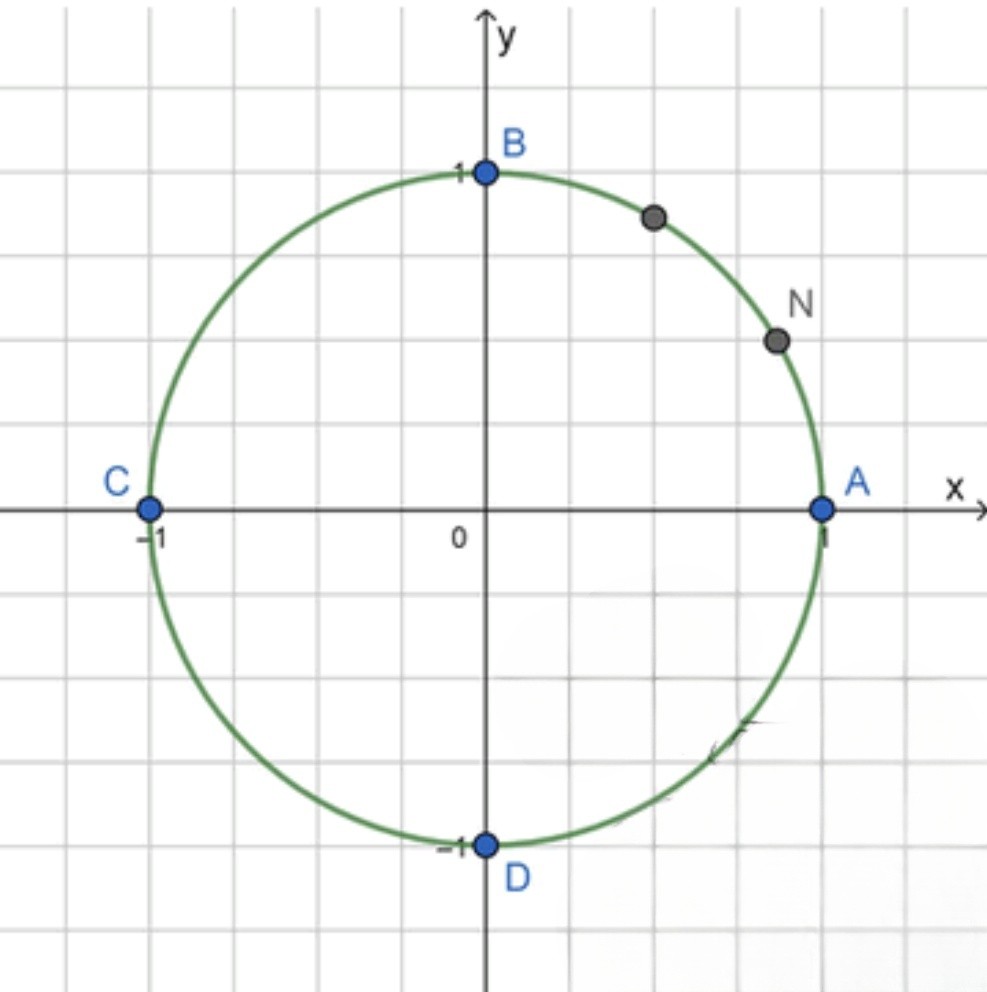
Шаг 3: Разделим дугу $AB$ на 3 равные части

$$\text{Одна часть} = \frac{1}{3} \cdot \frac{\pi}{2} = \frac{\pi}{6}.$$

Шаг 4: Чтобы получить $\frac{\pi}{6}$, берём одну такую часть:

$$AN = \frac{\pi}{6}.$$

Шаг 5: Отметим точку $N$

• Она ближе к точке $A$, чем к точке $B$, на 1/3 от всей дуги $AB$.

Ответ:

$$N = N\left(\frac{\pi}{6}\right)$$

г) $\frac{\pi}{8}$

Шаг 1: Дуга $AB = \frac{\pi}{2}$

Шаг 2: Требуется построить угол $\frac{\pi}{8}$

Шаг 3: Сначала разделим дугу $AB$ пополам

$$AK = \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4}.$$

• Это мы уже делали в пункте (б). Точка $K$ уже построена.

Шаг 4: Теперь разделим отрезок $AK$ ещё раз пополам

$$AP = \frac{1}{2} \cdot \frac{\pi}{4} = \frac{\pi}{8}.$$

Шаг 5: Отметим точку $P$

• Точка $P$ находится между точками $A$ и $K$, на четверть всей дуги $AB$, т.е. ближе к $A$.

Ответ:

$$P = P\left(\frac{\pi}{8}\right)$$