ГДЗ 10-11 Класс Номер 4.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Найдите на числовой окружности точку, которая соответствует заданному числу:

а) $\frac{2\pi }{3}$

б) $\frac{3\pi }{4}$

в) $\frac{5\pi }{6}$

г) $\frac{5\pi }{4}$$$

Изобразим окружность с основными точками:

а) $\frac{2\pi}{3} = \frac{\pi}{2} + \frac{\pi}{6}$;

Разделим $BC$ на три равных части:

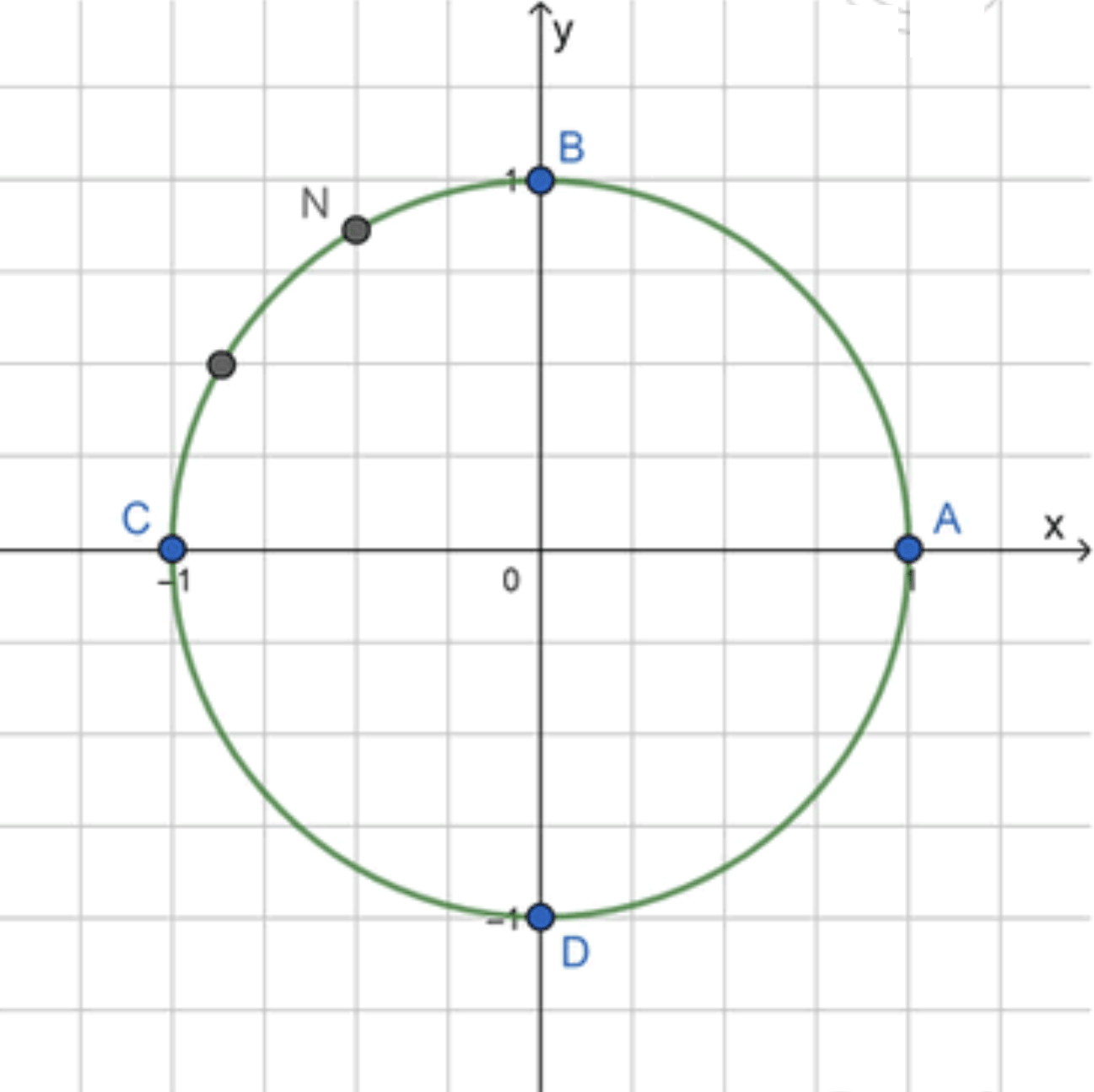
$$AN = AB + BN = \frac{\pi}{2} + \frac{1}{3} \cdot \frac{\pi}{2} = \frac{\pi}{2} + \frac{\pi}{6} = \frac{2\pi}{3}$$

Ответ: $N = N\left(\frac{2\pi}{3}\right)$.

б) $\frac{3\pi}{4} = \frac{\pi}{2} + \frac{\pi}{4}$;

Разделим $BC$ на две равные части:

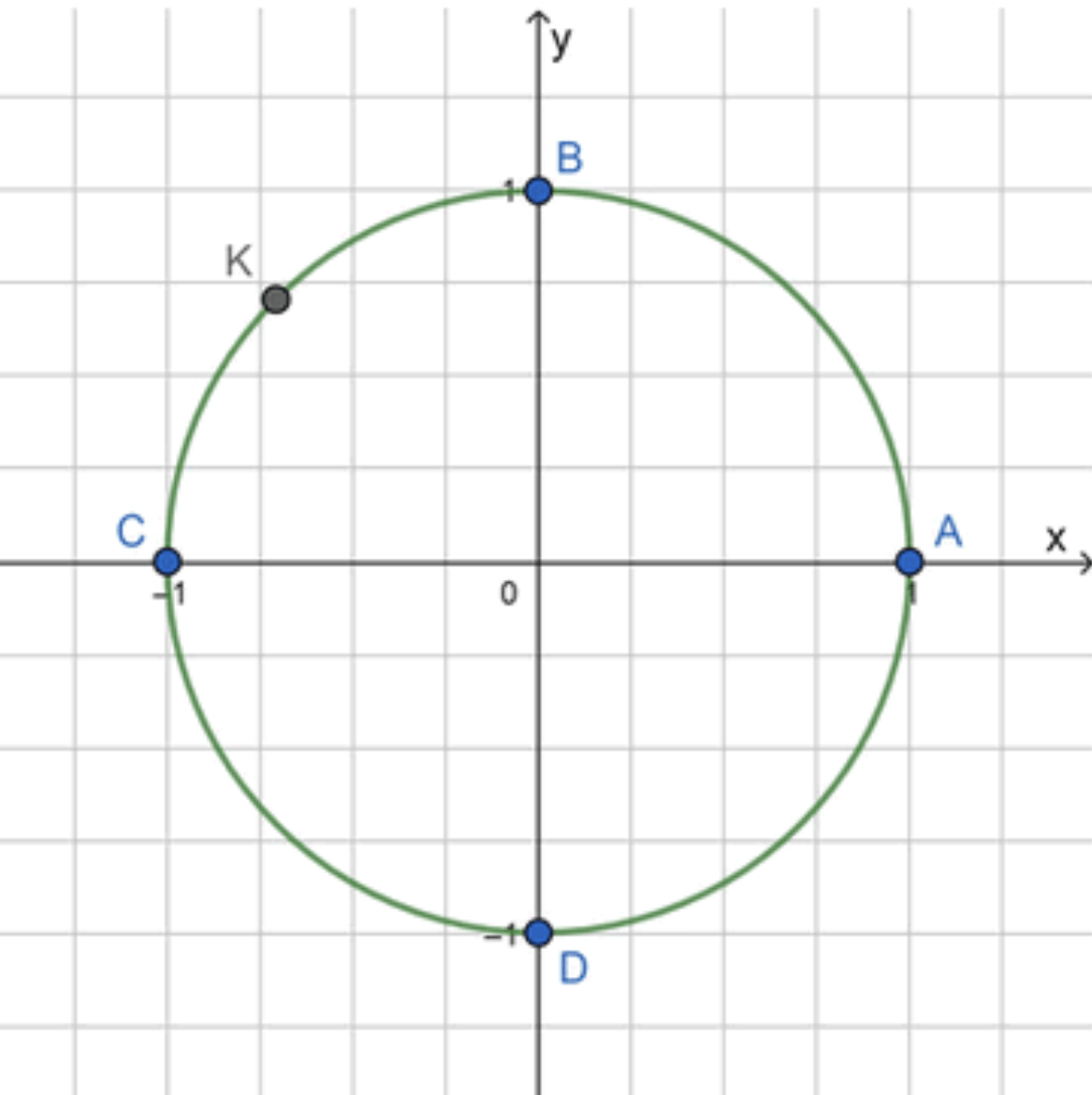
$$AK = AB + BK = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}$$

Ответ: $K = K\left(\frac{3\pi}{4}\right)$.

в) $\frac{5\pi}{6} = \pi + \frac{\pi}{3}$;

Разделим $BC$ на три равных части:

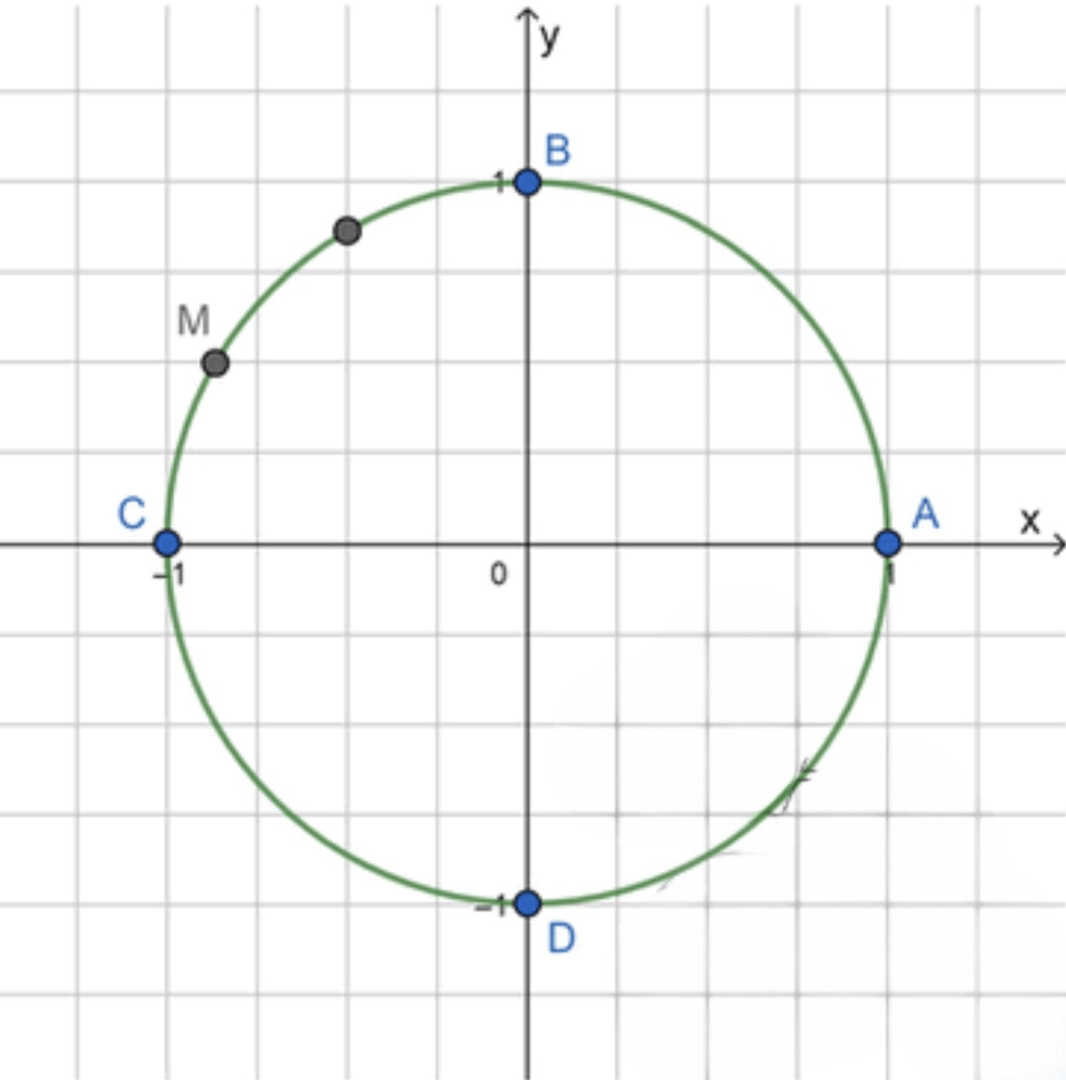
$$AM = AB + BM = \frac{\pi}{2} + \frac{2}{3} \cdot \frac{\pi}{2} = \frac{\pi}{2} + \frac{\pi}{3} = \frac{5\pi}{6}$$

Ответ: $M = M\left(\frac{5\pi}{6}\right)$.

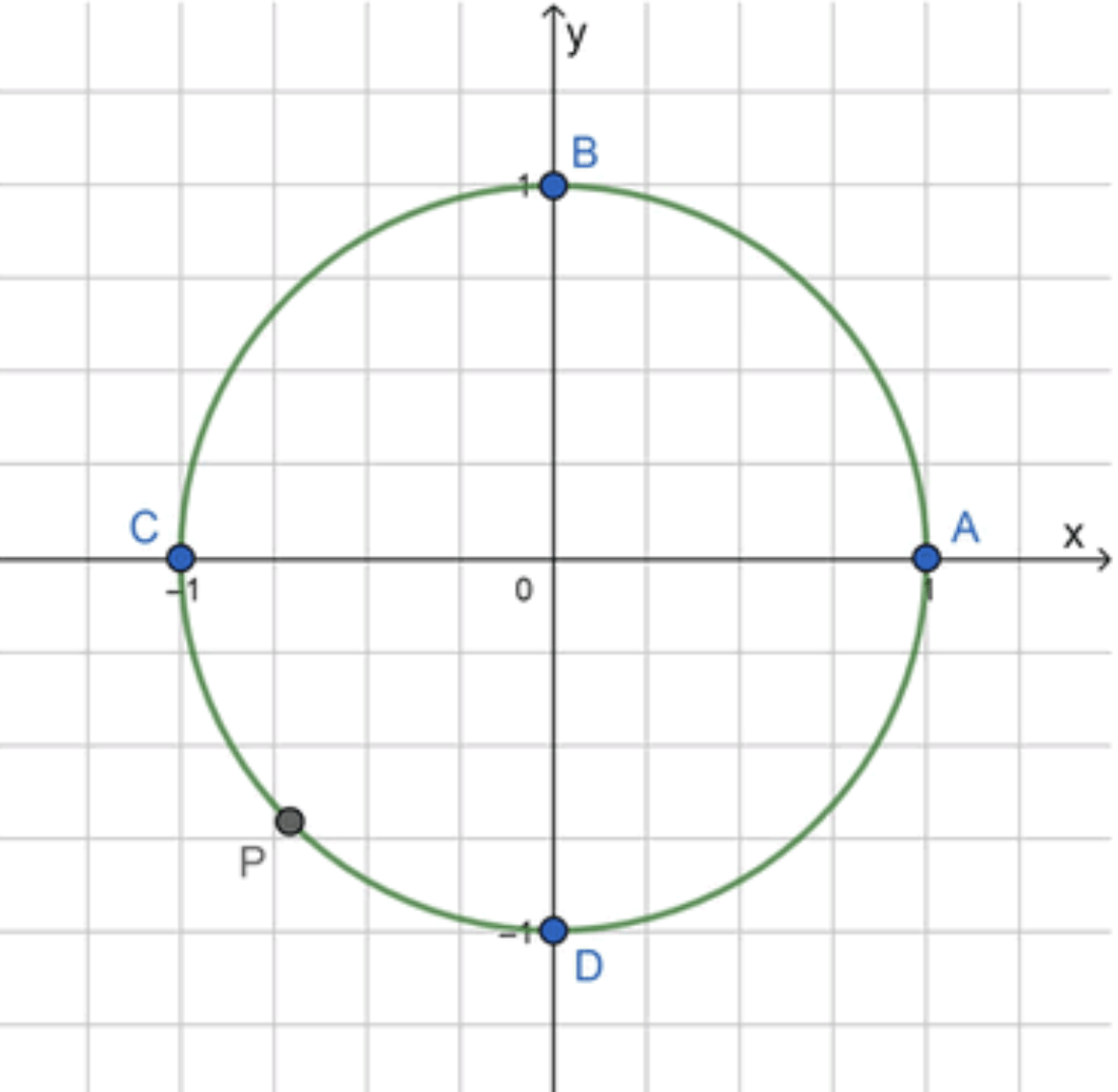
г) $\frac{5\pi}{4} = \pi + \frac{\pi}{4}$;

Разделим $CD$ на две равные части:

$$AP = AC + CP = \pi + \frac{\pi}{4} = \frac{5\pi}{4}$$

Ответ: $P = P\left(\frac{5\pi}{4}\right)$.

Основные точки — это точки, соответствующие углам кратным $\frac{\pi}{6}$, $\frac{\pi}{4}$, $\frac{\pi}{3}$, $\frac{\pi}{2}$, $\pi$, и так далее на единичной окружности.

На единичной окружности угол отсчитывается против часовой стрелки от положительного направления оси $Ox$.
Отметим базовые точки:

• $A = A(0)$ — начало отсчёта.
• $B = B\left(\frac{\pi}{2}\right)$ — вверх, на 90°.
• $C = C(\pi)$ — налево, на 180°.
• $D = D\left(\frac{3\pi}{2}\right)$ — вниз, на 270°.
• Вернувшись в $A$, угол будет $2\pi$ — полный круг.

а) $\frac{2\pi}{3} = \frac{\pi}{2} + \frac{\pi}{6}$

Цель: найти точку $N$, соответствующую углу $\frac{2\pi}{3}$.

Шаг 1: Анализ угла

$$\frac{2\pi}{3} = \frac{\pi}{2} + \frac{\pi}{6}$$

Это значит, что мы идём от $A$ сначала на угол $\frac{\pi}{2}$ (приходим в точку $B$), а потом ещё на $\frac{\pi}{6}$.

Шаг 2: Найти длину дуги $BC$

Дуга от $B\left(\frac{\pi}{2}\right)$ до $C(\pi)$ имеет угол:

$$\pi — \frac{\pi}{2} = \frac{\pi}{2}$$

Шаг 3: Разделить $BC$ на 3 части

$$\frac{\pi}{2} \div 3 = \frac{1}{3} \cdot \frac{\pi}{2} = \frac{\pi}{6}$$

Шаг 4: Перейти на одну часть дуги от $B$ к $C$

$$AN = AB + BN = \frac{\pi}{2} + \frac{\pi}{6} = \frac{2\pi}{3}$$

Ответ:

$$N = N\left(\frac{2\pi}{3}\right)$$

б) $\frac{3\pi}{4} = \frac{\pi}{2} + \frac{\pi}{4}$

Цель: найти точку $K$, соответствующую углу $\frac{3\pi}{4}$

Шаг 1: Анализ

Угол $\frac{3\pi}{4}$ — это угол чуть больше, чем $\frac{\pi}{2}$, находится во втором квадранте.

$$\frac{3\pi}{4} = \frac{\pi}{2} + \frac{\pi}{4}$$

Шаг 2: Длина дуги $BC$

$$BC = \frac{\pi}{2}$$

Шаг 3: Разделим $BC$ на 2 части

$$\frac{\pi}{2} \div 2 = \frac{\pi}{4}$$

Шаг 4: Перейдём от $B$ к $C$ на одну часть

$$AK = AB + BK = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}$$

Ответ:

$$K = K\left(\frac{3\pi}{4}\right)$$

в) $\frac{5\pi}{6} = \frac{\pi}{2} + \frac{\pi}{3}$

Цель: найти точку $M$, соответствующую углу $\frac{5\pi}{6}$

Важно: в оригинале ошибка!

Правильное разложение:

$$\frac{5\pi}{6} = \frac{\pi}{2} + \frac{\pi}{3}$$

а не $\pi + \frac{\pi}{3}$

Шаг 1: Проверим сумму

$$\frac{\pi}{2} + \frac{\pi}{3} = \frac{3\pi + 2\pi}{6} = \frac{5\pi}{6}$$

Шаг 2: Длина дуги $BC = \frac{\pi}{2}$

Шаг 3: Разделим $BC$ на 3 части

$$\frac{\pi}{2} \div 3 = \frac{1}{3} \cdot \frac{\pi}{2} = \frac{\pi}{6}$$

Чтобы пройти $\frac{\pi}{3}$ по дуге $BC$, нужно взять:

$$\frac{\pi}{3} \div \frac{\pi}{6} = 2 \text{ части}$$

Шаг 4: Двигаемся на 2 части от $B$

$$AM = AB + BM = \frac{\pi}{2} + 2 \cdot \frac{\pi}{6} = \frac{\pi}{2} + \frac{\pi}{3} = \frac{5\pi}{6}$$

Ответ:

$$M = M\left(\frac{5\pi}{6}\right)$$

г) $\frac{5\pi}{4} = \pi + \frac{\pi}{4}$

Цель: найти точку $P$, соответствующую углу $\frac{5\pi}{4}$

Шаг 1: Анализ

$$\frac{5\pi}{4} = \pi + \frac{\pi}{4}$$

Угол $\pi$ — это точка $C$, а $\frac{5\pi}{4}$ — точка на дуге от $C$ к $D$ (третий квадрант)

Шаг 2: Длина дуги $CD = \frac{3\pi}{2} — \pi = \frac{\pi}{2}$

Шаг 3: Разделим $CD$ на 2 части

$$\frac{\pi}{2} \div 2 = \frac{\pi}{4}$$

Шаг 4: Перейдём от $C$ к $D$ на одну часть

$$AP = AC + CP = \pi + \frac{\pi}{4} = \frac{5\pi}{4}$$

Ответ:

$$P=P\left(\frac{5\pi }{4}\right)$$