ГДЗ 10-11 Класс Номер 4.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Найдите на числовой окружности точку, которая соответствует заданному числу:

а) $\frac{4\pi }{3}$

б) $\frac{5\pi }{3}$

в) $\frac{7\pi }{6}$

г) $\frac{11\pi }{6}$

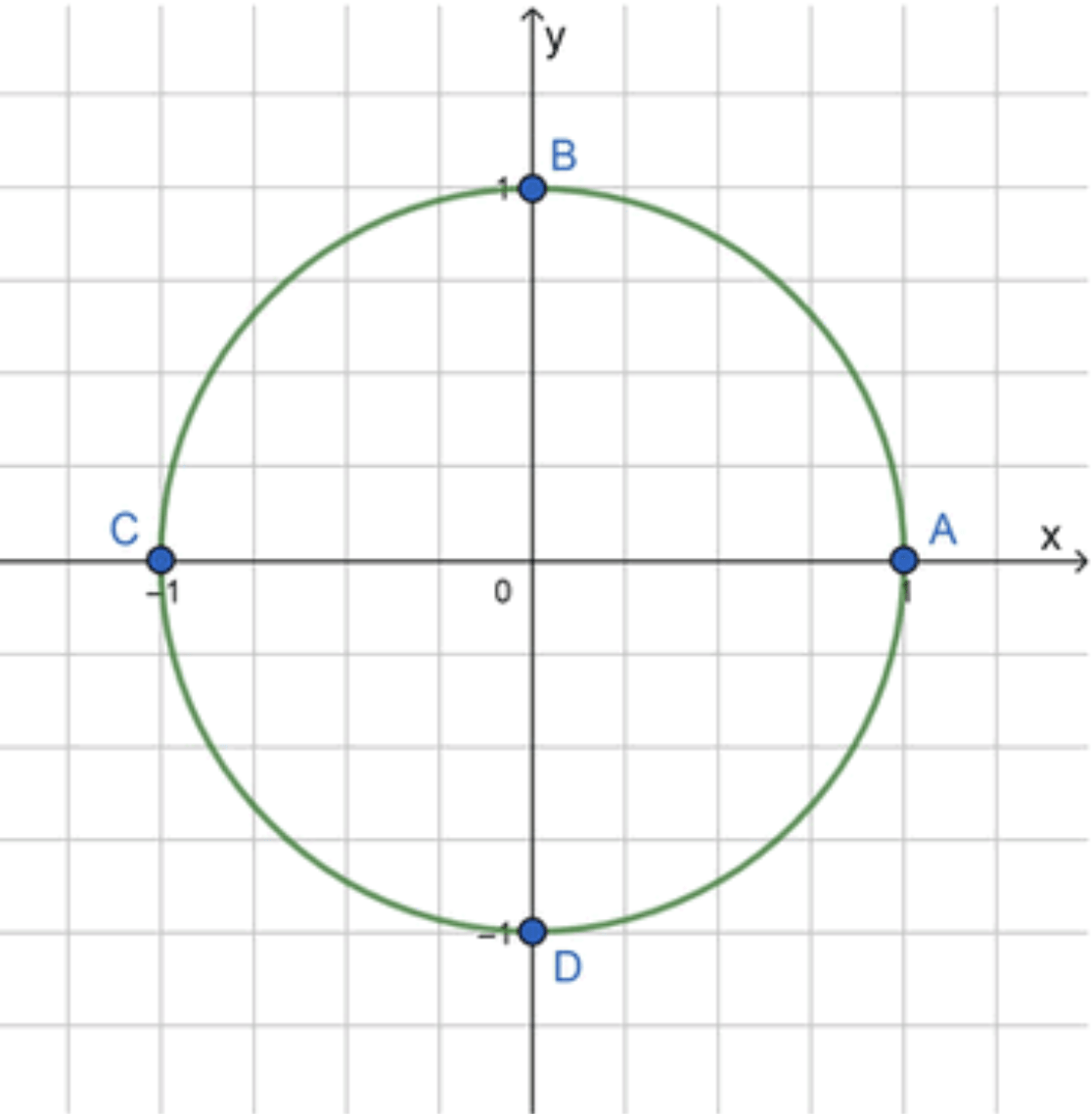
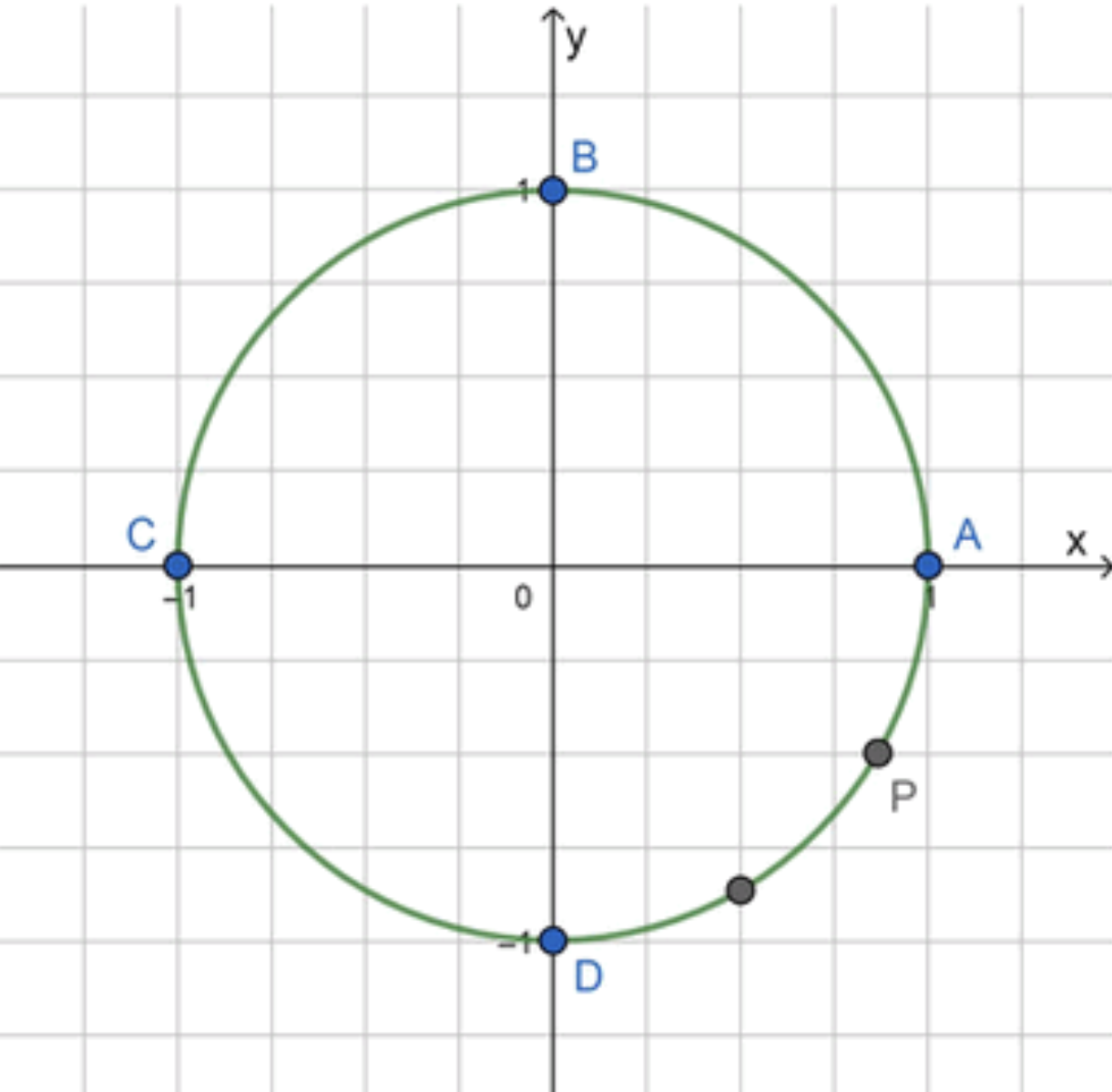
Изобразим окружность с основными точками:

а) $\frac{4\pi}{3} = \pi + \frac{\pi}{3}$;
Разделим $CD$ на три равных части:

$$AN = AC + CN = \pi + \frac{2}{3} \cdot \frac{\pi}{2} = \pi + \frac{\pi}{3} = \frac{4\pi}{3};$$

Ответ: $N = N\left(\frac{4\pi}{3}\right)$.

б) $\frac{5\pi}{3} = \frac{3\pi}{2} + \frac{\pi}{6}$;
Разделим $DA$ на три равных части:

$$AK = AD + DK = \frac{3\pi}{2} + \frac{1}{3} \cdot \frac{\pi}{2} = \frac{3\pi}{2} + \frac{\pi}{6} = \frac{5\pi}{3};$$

Ответ: $K = K\left(\frac{5\pi}{3}\right)$.

в) $\frac{7\pi}{6} = \pi + \frac{\pi}{6}$;
Разделим $CD$ на три равных части:

$$AM = AC + CM = \pi + \frac{1}{3} \cdot \frac{\pi}{2} = \pi + \frac{\pi}{6} = \frac{7\pi}{6};$$

Ответ: $M = M\left(\frac{7\pi}{6}\right)$.

г) $\frac{11\pi}{6} = \frac{3\pi}{2} + \frac{\pi}{3}$;
Разделим $DA$ на три равных части:

$$AP = AD + DP = \frac{3\pi}{2} + \frac{2}{3} \cdot \frac{\pi}{2} = \frac{3\pi}{2} + \frac{\pi}{3} = \frac{11\pi}{6};$$

Ответ: $P = P\left(\frac{11\pi}{6}\right)$.

а) Найти точку, соответствующую углу $\frac{4\pi}{3}$

Шаг 1: Разложим угол

$$\frac{4\pi}{3} = \pi + \frac{\pi}{3}$$

То есть угол $\frac{4\pi}{3}$ расположен в третьей четверти — сразу после $\pi$, но не доходя до $\frac{3\pi}{2}$.

Шаг 2: Уточним путь вдоль окружности

• От $A$ до $C$ (т.е. от $0$ до $\pi$) — это половина окружности.
• От $C$ до $D$ — это ещё $\frac{\pi}{2}$ (четверть окружности).

Значит, чтобы дойти от $C$ до нужного угла $\frac{4\pi}{3}$, нужно пройти дополнительную часть отрезка $CD$.

Шаг 3: Найдём, какую долю от $CD$ нужно пройти

$$\frac{4\pi}{3} — \pi = \frac{\pi}{3}$$

Значит, мы находимся на расстоянии $\frac{\pi}{3}$ от точки $C$.

Так как весь отрезок $CD = \frac{\pi}{2}$, а $\frac{\pi}{3} = \frac{2}{3} \cdot \frac{\pi}{2}$, то:

$$\text{Доля отрезка } CD: \quad \frac{\pi}{3} = \frac{2}{3} \cdot \frac{\pi}{2}$$

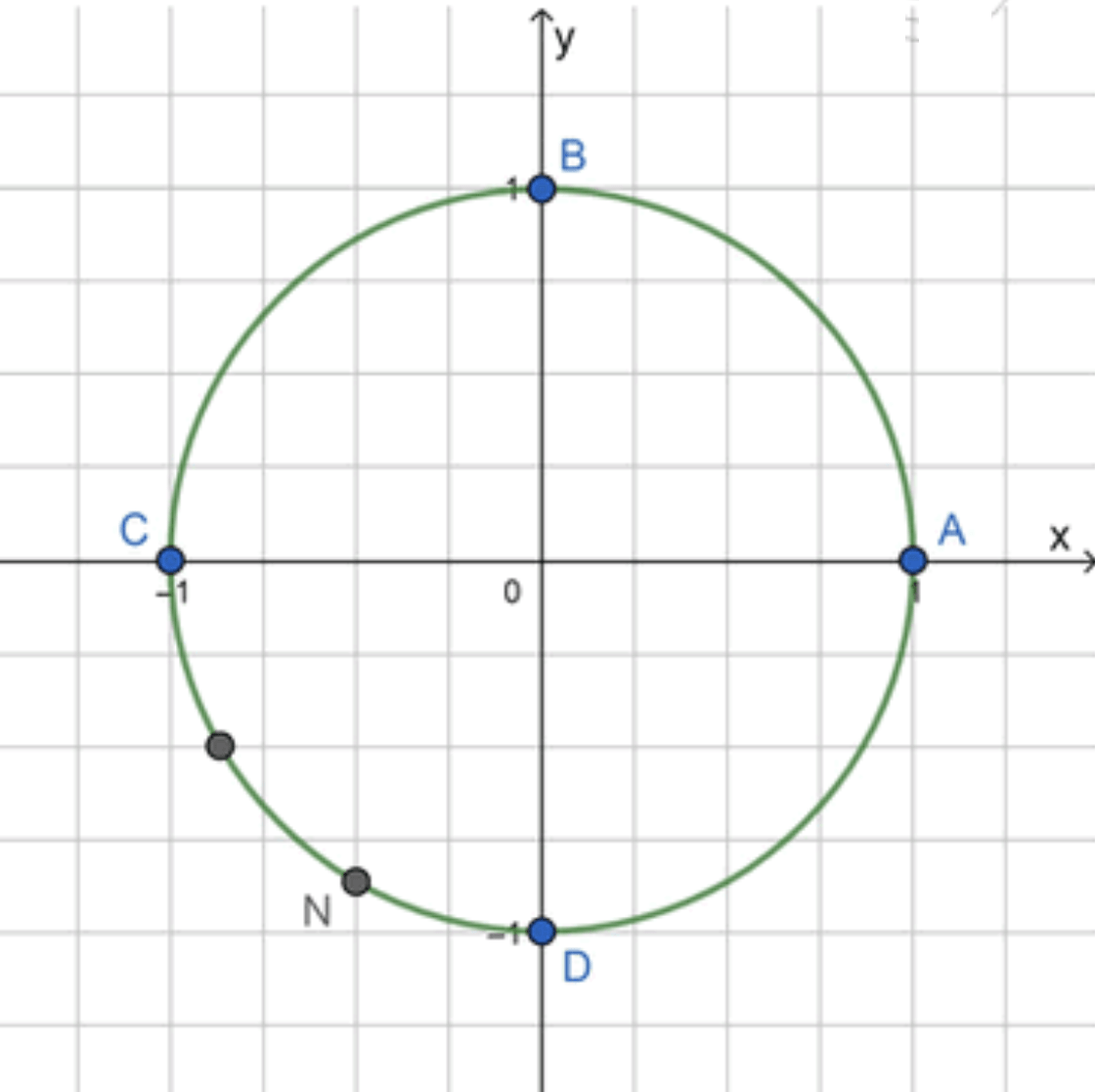
Шаг 4: Обозначим эту точку как $N$

Путь от точки $A$ до точки $N$:

$$AN = AC + CN = \pi + \frac{2}{3} \cdot \frac{\pi}{2} = \pi + \frac{\pi}{3} = \frac{4\pi}{3}$$

Ответ: $N = N\left(\frac{4\pi}{3}\right)$

б) Найти точку, соответствующую углу $\frac{5\pi}{3}$

Шаг 1: Разложим угол

$$\frac{5\pi}{3} = \frac{3\pi}{2} + \frac{\pi}{6}$$

То есть угол находится в четвёртой четверти, между $\frac{3\pi}{2}$ и $2\pi$.

Шаг 2: Пройденный путь

• От $A$ до $D$ — это $\frac{3\pi}{2}$,
• После этого надо пройти ещё $\frac{\pi}{6}$.

Шаг 3: Уточним, какую долю отрезка $DA$ надо пройти

• Отрезок $DA = \frac{\pi}{2}$,
• $\frac{\pi}{6} = \frac{1}{3} \cdot \frac{\pi}{2}$

Значит, нужно пройти треть отрезка $DA$.

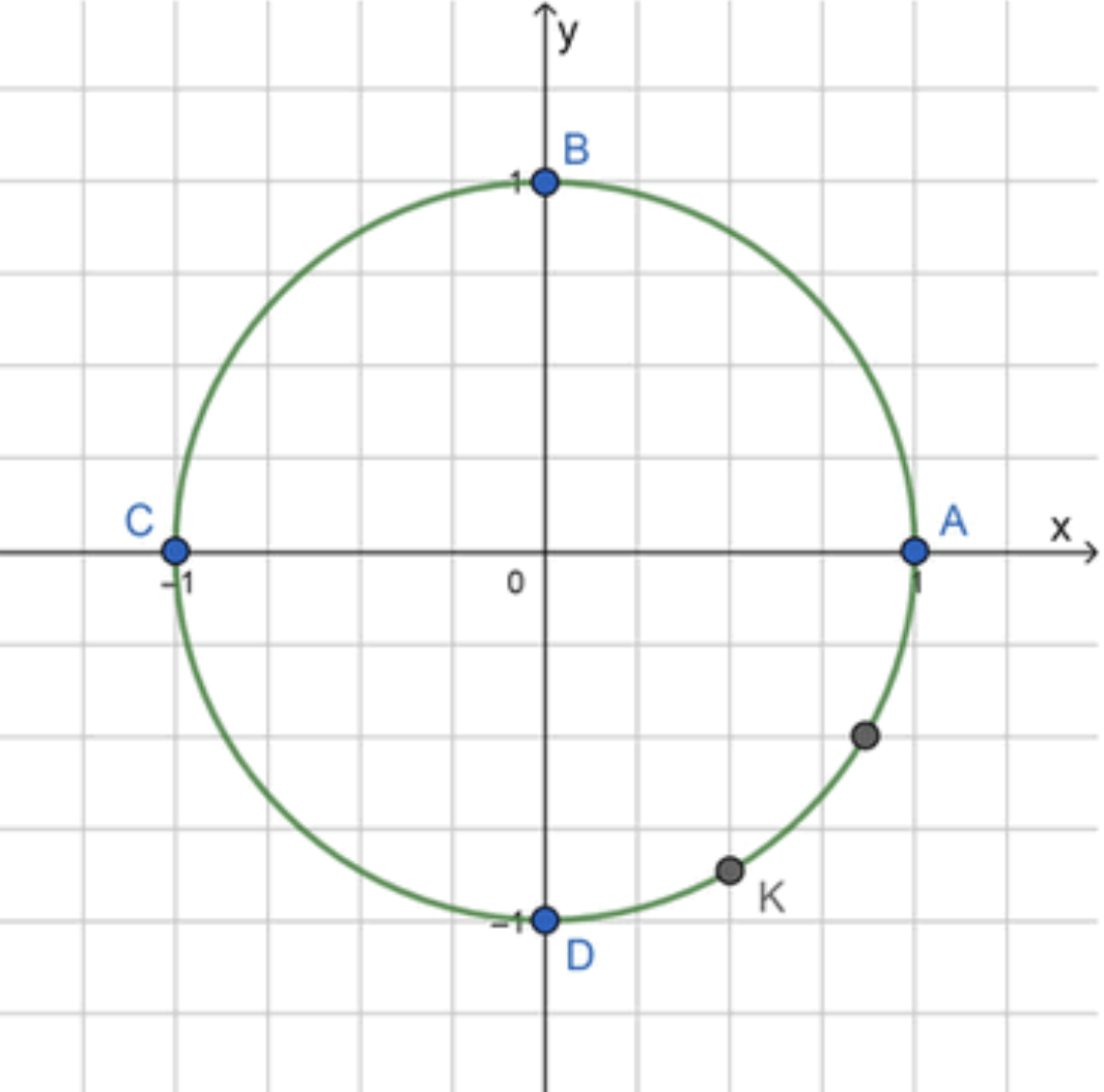
Шаг 4: Обозначим эту точку как $K$

$$AK = AD + DK = \frac{3\pi}{2} + \frac{1}{3} \cdot \frac{\pi}{2} = \frac{3\pi}{2} + \frac{\pi}{6} = \frac{5\pi}{3}$$

Ответ: $K = K\left(\frac{5\pi}{3}\right)$

в) Найти точку, соответствующую углу $\frac{7\pi}{6}$

Шаг 1: Разложим угол

$$\frac{7\pi}{6} = \pi + \frac{\pi}{6}$$

Угол находится в третьей четверти, между $\pi$ и $\frac{3\pi}{2}$.

Шаг 2: Определим расстояние от $\pi$

$$\frac{7\pi}{6} — \pi = \frac{\pi}{6}$$

Отрезок $CD = \frac{\pi}{2}$, а $\frac{\pi}{6} = \frac{1}{3} \cdot \frac{\pi}{2}$

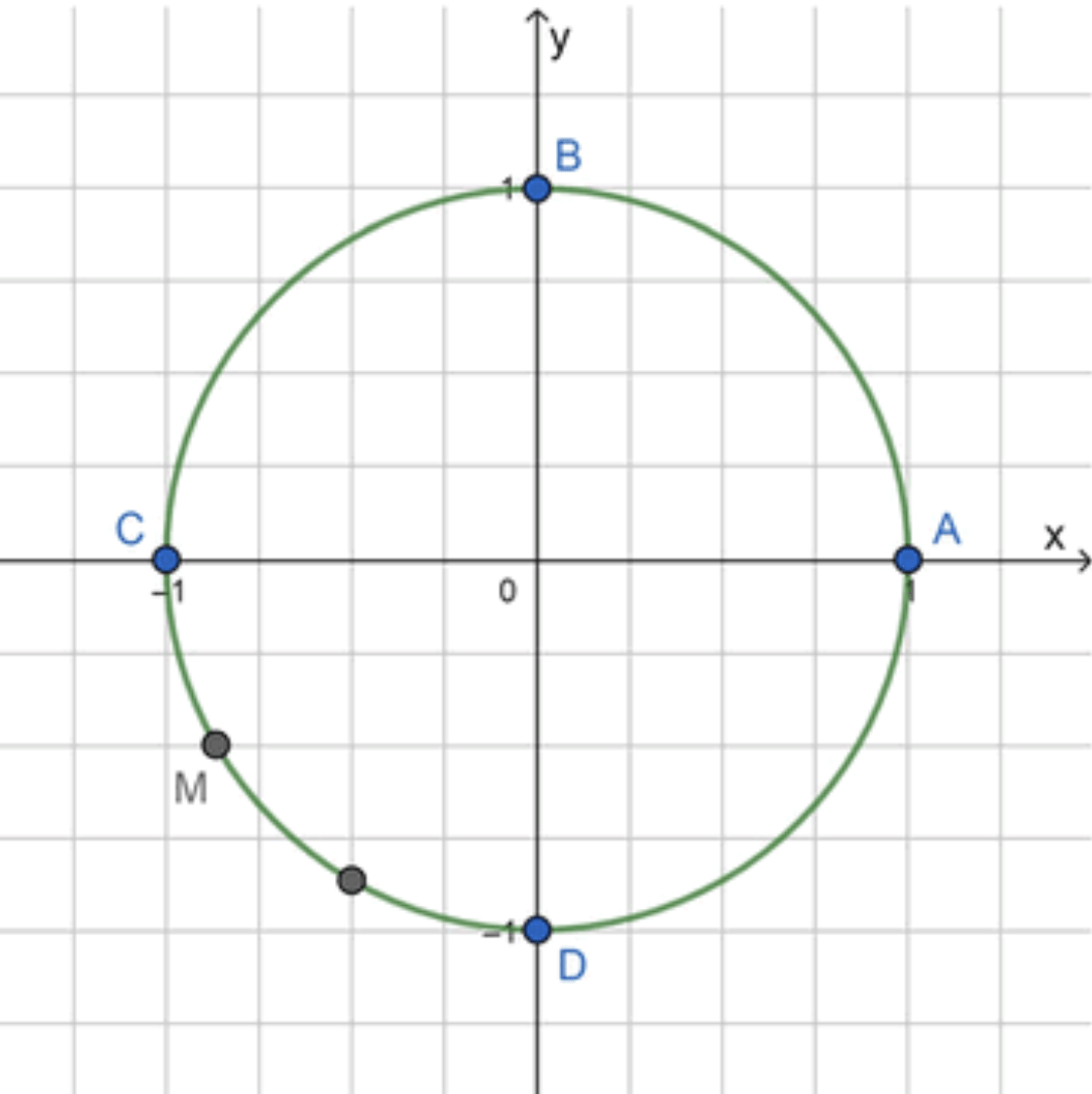
Шаг 3: Обозначим точку как $M$

$$AM = AC + CM = \pi + \frac{1}{3} \cdot \frac{\pi}{2} = \pi + \frac{\pi}{6} = \frac{7\pi}{6}$$

Ответ: $M = M\left(\frac{7\pi}{6}\right)$

г) Найти точку, соответствующую углу $\frac{11\pi}{6}$

Шаг 1: Разложим угол

$$\frac{11\pi}{6} = \frac{3\pi}{2} + \frac{\pi}{3}$$

Это четвёртая четверть (между $\frac{3\pi}{2}$ и $2\pi$).

Шаг 2: Определим, какую часть отрезка $DA$ нужно пройти

• $\frac{\pi}{3} = \frac{2}{3} \cdot \frac{\pi}{2}$

Шаг 3: Обозначим точку как $P$

$$AP = AD + DP = \frac{3\pi}{2} + \frac{2}{3} \cdot \frac{\pi}{2} = \frac{3\pi}{2} + \frac{\pi}{3} = \frac{11\pi}{6}$$

Ответ: $P = P\left(\frac{11\pi}{6}\right)$