ГДЗ 10-11 Класс Номер 40.24 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $\left(\frac{1}{2}\right)^x = 0{,}5x + 5$;

б) $3^x = -x + 4$;

в) $\left(\frac{1}{7}\right)^x = 2x + 9$;

г) $3^{\frac{x}{2}} = -0{,}5x + 4$

Решить уравнение:

а) $\left(\frac{1}{2}\right)^x = 0{,}5x + 5$;

$y = \left(\frac{1}{2}\right)^x$ — показательная функция:

$y = 0{,}5x + 5$ — уравнение прямой:

Графики функций:

Ответ: $-2$.

б) $3^x = -x + 4$;

Функция $f(x) = 3^x$ возрастает на $R$;
Функция $g(x) = -x + 4$ убывает на $R$;

Методом перебора найдем пересечение:
$f(1) = 3^1 = 3$;
$g(1) = -1 + 4 = 3$;

Ответ: $1$.

в) $\left(\frac{1}{7}\right)^x = 2x + 9$;

Функция $f(x) = \left(\frac{1}{7}\right)^x$ убывает на $R$;
Функция $g(x) = 2x + 9$ возрастает на $R$;

Методом перебора найдем пересечение:
$f(-1) = \left(\frac{1}{7}\right)^{-1} = 7$;
$g(-1) = 2 \cdot (-1) + 9 = 7$;

Ответ: $-1$.

г) $3^{\frac{x}{2}} = -0{,}5x + 4$;
$(\sqrt{3})^x = -0{,}5x + 4$;

Функция $f(x) = (\sqrt{3})^x$ возрастает на $R$;
Функция $g(x) = -0{,}5x + 4$ убывает на $R$;

Методом перебора найдем пересечение:
$f(2) = (\sqrt{3})^2 = 3$;
$g(2) = -0{,}5 \cdot 2 + 4 = 3$;

Ответ: $2$.

а) $\left(\dfrac{1}{2}\right)^x = 0{,}5x + 5$

Шаг 1: Анализ функций

Левая часть — показательная функция:

$$f(x) = \left(\dfrac{1}{2}\right)^x$$

— Основание $\frac{1}{2} < 1$, поэтому функция убывает на всей числовой прямой $\mathbb{R}$.
— Значения всегда положительные: $f(x) > 0$ при любом $x$.
— Например:

$$f(-3) = \left(\dfrac{1}{2}\right)^{-3} = 2^3 = 8$$ $$f(-2) = \left(\dfrac{1}{2}\right)^{-2} = 2^2 = 4$$ $$f(0) = \left(\dfrac{1}{2}\right)^0 = 1$$

Правая часть — линейная функция:

$$g(x) = 0{,}5x + 5$$

— Прямая, возрастает (положительный коэффициент при $x$).
— Можно построить по точкам:

$$g(-4) = 0{,}5 \cdot (-4) + 5 = -2 + 5 = 3$$ $$g(0) = 0{,}5 \cdot 0 + 5 = 5$$

Шаг 2: Графическое представление

Шаг 3: Найдём точку пересечения методом подстановки

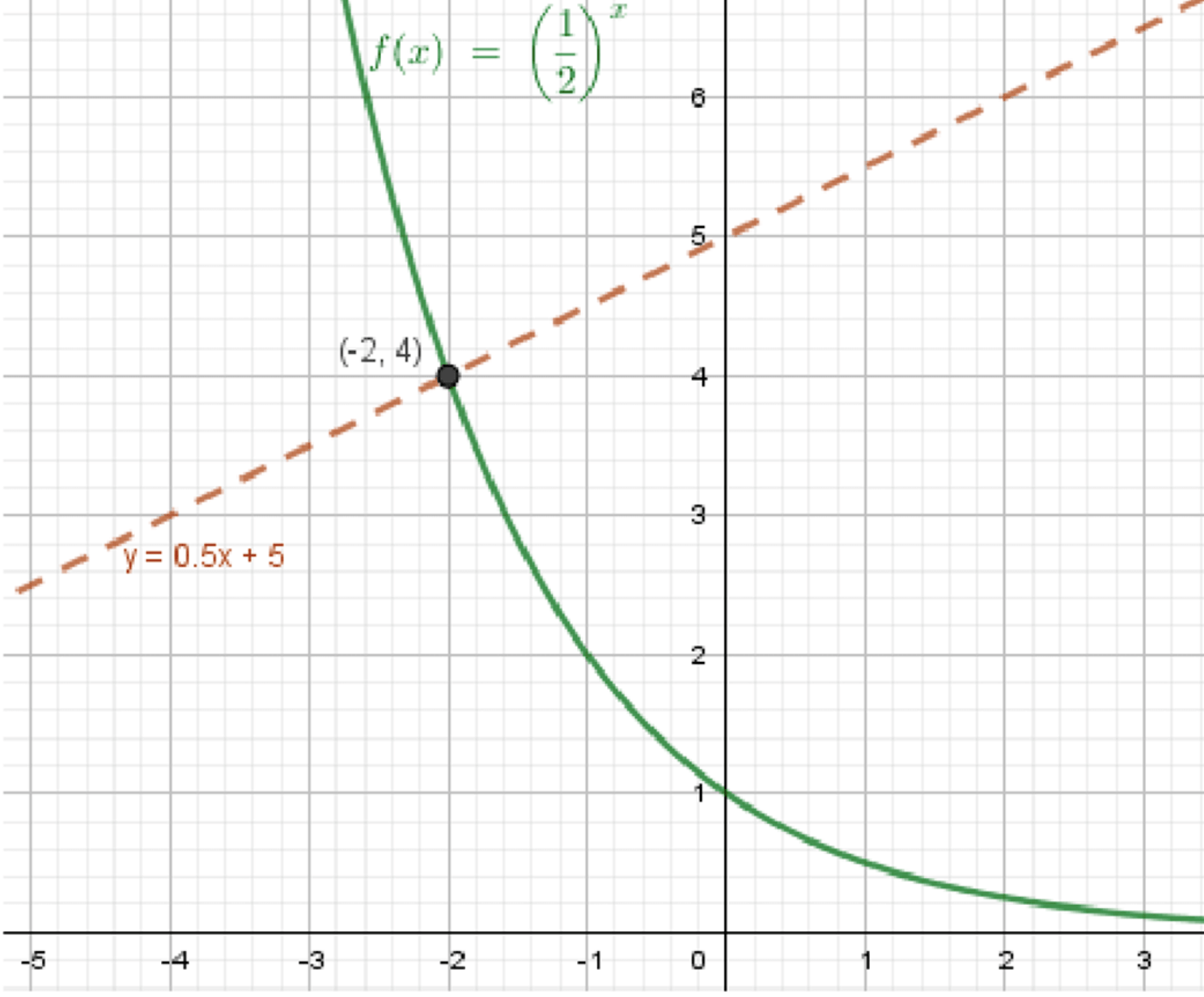
Проверим $x = -2$:

— Левая часть:

$$\left(\dfrac{1}{2}\right)^{-2} = 2^2 = 4$$

— Правая часть:

$$0{,}5 \cdot (-2) + 5 = -1 + 5 = 4$$ $$f(-2) = g(-2) = 4$$

Шаг 4: Вывод

Так как одна функция убывает, а вторая возрастает, пересечение только в одной точке.

Ответ: $-2$

б) $3^x = -x + 4$

Шаг 1: Анализ функций

Левая часть:

$$f(x) = 3^x$$

— Показательная функция с основанием $3 > 1$, возрастает на $\mathbb{R}$
— Значения положительные: $f(x) > 0$

Правая часть:

$$g(x) = -x + 4$$

— Линейная функция
— Коэффициент при $x$ отрицательный, поэтому убывает

Шаг 2: Проверим конкретное значение

Пусть $x = 1$:

— Левая часть:

$$3^1 = 3$$

— Правая часть:

$$-1 + 4 = 3$$ $$f(1) = g(1) = 3$$

Шаг 3: Вывод

Так как одна функция возрастает, а вторая убывает, решение только одно.

Ответ: $1$

в) $\left(\dfrac{1}{7}\right)^x = 2x + 9$

Шаг 1: Анализ функций

Левая часть:

$$f(x) = \left(\dfrac{1}{7}\right)^x$$

— Показательная функция, $\frac{1}{7} < 1$, значит убывает
— Значения $> 0$

Правая часть:

$$g(x) = 2x + 9$$

— Линейная, $k = 2 > 0$, значит возрастает

Шаг 2: Проверим значение $x = -1$

— Левая часть:

$$\left(\dfrac{1}{7}\right)^{-1} = 7$$

— Правая часть:

$$2 \cdot (-1) + 9 = -2 + 9 = 7$$ $$f(-1) = g(-1) = 7$$

Шаг 3: Вывод

Одна функция убывает, другая возрастает ⇒ пересечение в одной точке

Ответ: $-1$

г) $3^{\frac{x}{2}} = -0{,}5x + 4$

Шаг 1: Преобразуем левую часть

Запишем через корень:

$$3^{\frac{x}{2}} = (\sqrt{3})^x$$

Итак, уравнение:

$$(\sqrt{3})^x = -0{,}5x + 4$$

Левая часть — показательная функция:

$$f(x) = (\sqrt{3})^x$$

— Основание $\sqrt{3} > 1$ ⇒ функция возрастает

Правая часть — линейная:

$$g(x) = -0{,}5x + 4$$

— Коэффициент отрицателен ⇒ функция убывает

Шаг 2: Подстановка $x = 2$

— Левая часть:

$$(\sqrt{3})^2 = 3$$

— Правая часть:

$$-0{,}5 \cdot 2 + 4 = -1 + 4 = 3$$ $$f(2) = g(2) = 3$$

Шаг 3: Вывод

Функции возрастающая и убывающая ⇒ одна точка пересечения

Ответ: $2$