Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 40.53 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) ;
б) ;
в) ;
г)
Решить неравенство:
а) ;
Функция возрастает на ;
Функция убывает на ;
Методом перебора найдем пересечение:
;
;
Ответ: .
б) ;
Функция убывает на ;
Функция возрастает на ;
Методом перебора найдем пересечение:
;
;
Ответ: .
в) ;
Функция возрастает на ;
Функция убывает на ;
Методом перебора найдем пересечение:
;
;
Ответ: .
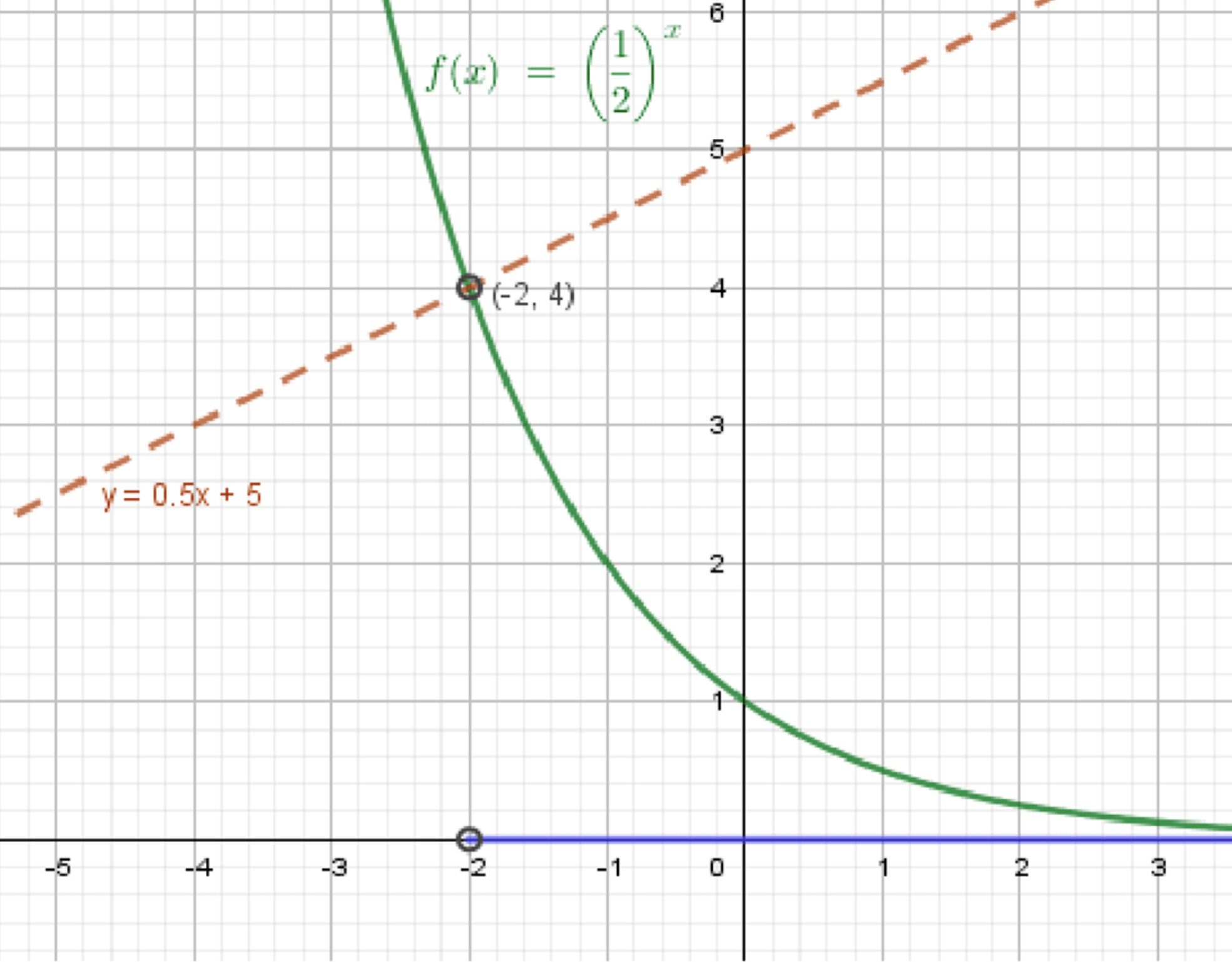
г) ;
— показательная функция:
— уравнение прямой:
Графики функций:
Ответ:
а) Решить неравенство:
Шаг 1. Функция — показательная, с основанием . Она возрастает на всей числовой прямой.
Шаг 2. Функция — линейная. Коэффициент при отрицателен, значит функция убывает на всей числовой прямой.
Шаг 3. При :
То есть графики пересекаются при .
Шаг 4. Так как возрастает, а убывает, то:
- При :
- При :
Следовательно: неравенство выполняется при
Ответ:
б) Решить неравенство:
Шаг 1. Функция — убывающая показательная функция (основание ).
Шаг 2. Функция — возрастающая линейная.
Шаг 3. Найдём точку пересечения, подставим :
Значит, графики пересекаются в точке
Шаг 4. Для :
- увеличивается
- уменьшается
⇒
Для :
- убывает
- растёт
⇒
Следовательно: неравенство выполняется при
Ответ:
в) Решить неравенство:
Шаг 1. Функция — показательная возрастающая.
Шаг 2. Функция — убывающая линейная.
Шаг 3. Найдём точку пересечения:
При :
Значит, пересекаются в точке
Шаг 4. Для :
- увеличивается
- уменьшается
⇒
Для :
- уменьшается
- увеличивается
⇒
Следовательно: неравенство выполняется при
Ответ:
г) Решить неравенство:
Шаг 1. Построим значения функции :
Шаг 2. Построим значения функции :
Шаг 3. Найдём точку пересечения. Проверим при :
Пересекаются при
Шаг 4. Функция убывает, — возрастает.
Значит:
- При : ⇒ неравенство выполняется
- При :
Следовательно: неравенство выполняется при
Ответ: