ГДЗ 10-11 Класс Номер 41.22 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y={\log }_x{x}^2\mathrm{}$

б) $y=2^{{\log }_{2}x}$

в) $y=x^{{\log }_{x}2}$

г) $y={\log }_x\frac{1}{x}$

Построить график функции:

а) $y = \log_x x^2 = 2$;
Выражение имеет смысл при:
$x > 0$;
График функции:

б) $y = 2^{\log_2 x} = x$;
Выражение имеет смысл при:
$x > 0$;
График функции:

в) $y = x^{\log_x 2} = 2$;
Выражение имеет смысл при:
$x > 0$;
График функции:

г) $y = \log_x \frac{1}{x} = \log_x x^{-1} = -1$;
Выражение имеет смысл при:
$x > 0$;
График функции:

а) $y = \log_x x^2 = 2$

Шаг 1. Анализ области определения.

Выражение $\log_x x^2$ имеет смысл при:

• $x > 0$ — основание логарифма положительное;
• $x \ne 1$ — основание логарифма не может быть равно 1 (логарифм не определён);
• $x^2 > 0$ — подлогарифмическое выражение положительно всегда при $x \ne 0$, но $x = 0$ исключается из-за первого условия.

Итак, область определения:

$$x > 0,\ x \ne 1$$

Шаг 2. Решим уравнение:

$$\log_x x^2 = 2$$

Используем свойство логарифма:

$$\log_x x^2 = 2 \cdot \log_x x = 2 \cdot 1 = 2$$

Проверка: работает при любом $x > 0, x \ne 1$

Или решим иначе:

$$\log_x x^2 = 2 \iff x^2 = x^2$$

Это тождество, которое верно при любом $x > 0, x \ne 1$

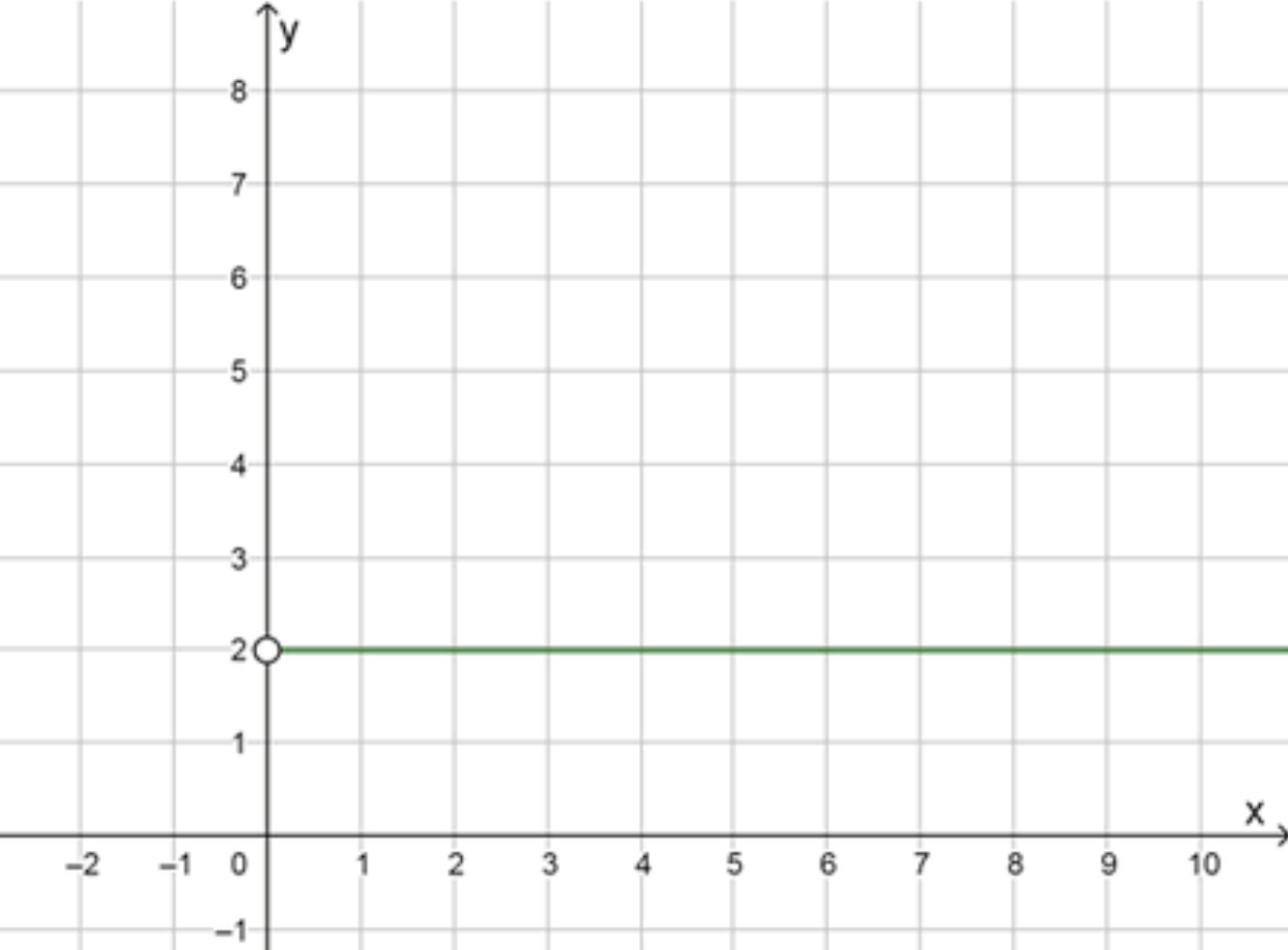
Шаг 3. Описание графика

График — это горизонтальная прямая $y = 2$, но не на всей числовой оси, а только на области:

$$x > 0,\ x \ne 1$$

Особенность:
В точке $x = 1$ — разрыв, потому что логарифм по основанию 1 не определён.

б) $y = 2^{\log_2 x} = x$

Шаг 1. Область определения

$\log_2 x$ определён только при $x > 0$

Итак, область определения:

$$x > 0$$

Шаг 2. Преобразуем выражение:

$$y = 2^{\log_2 x}$$

Используем основное логарифмическое тождество:

$$a^{\log_a x} = x \quad (a > 0, a \ne 1,\ x > 0)$$

Здесь $a = 2$, всё подходит:

$$y = x$$

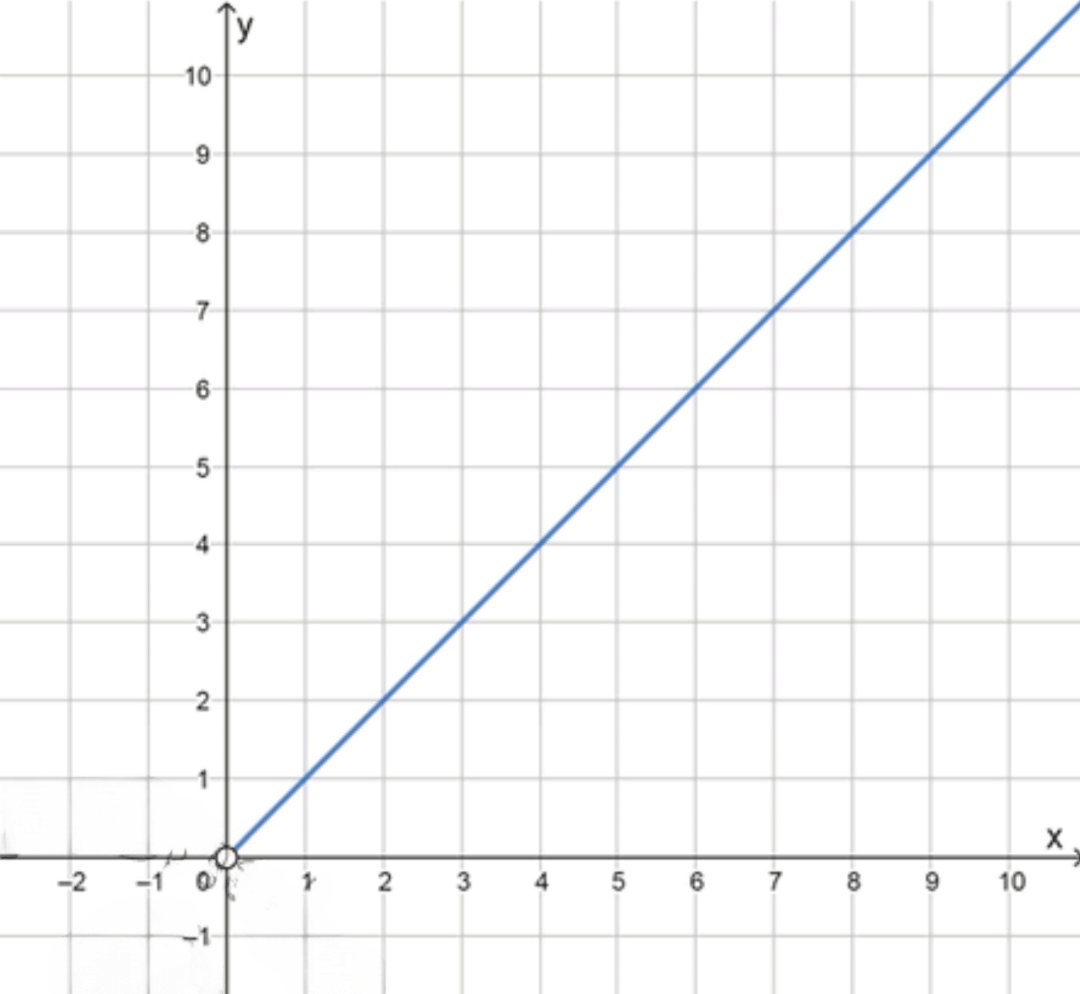
Шаг 3. Описание графика

Это прямая $y = x$, но не на всей оси, а только на:

$$x > 0$$

Особенность:
Начинается от положительных $x$, проходит через точку $(1, 1)$, не включает отрицательные значения.

в) $y = x^{\log_x 2} = 2$

Шаг 1. Область определения

• $x > 0$ — основание логарифма;
• $x \ne 1$ — логарифм не определён при $\log_1 2$;
• степень $\log_x 2$ существует, когда $x > 0,\ x \ne 1$

Итак, область определения:

$$x > 0,\ x \ne 1$$

Шаг 2. Преобразуем:

$$y = x^{\log_x 2}$$

Используем тождество:

$$x^{\log_x 2} = 2$$

Это тождество выполняется при всех допустимых $x$.

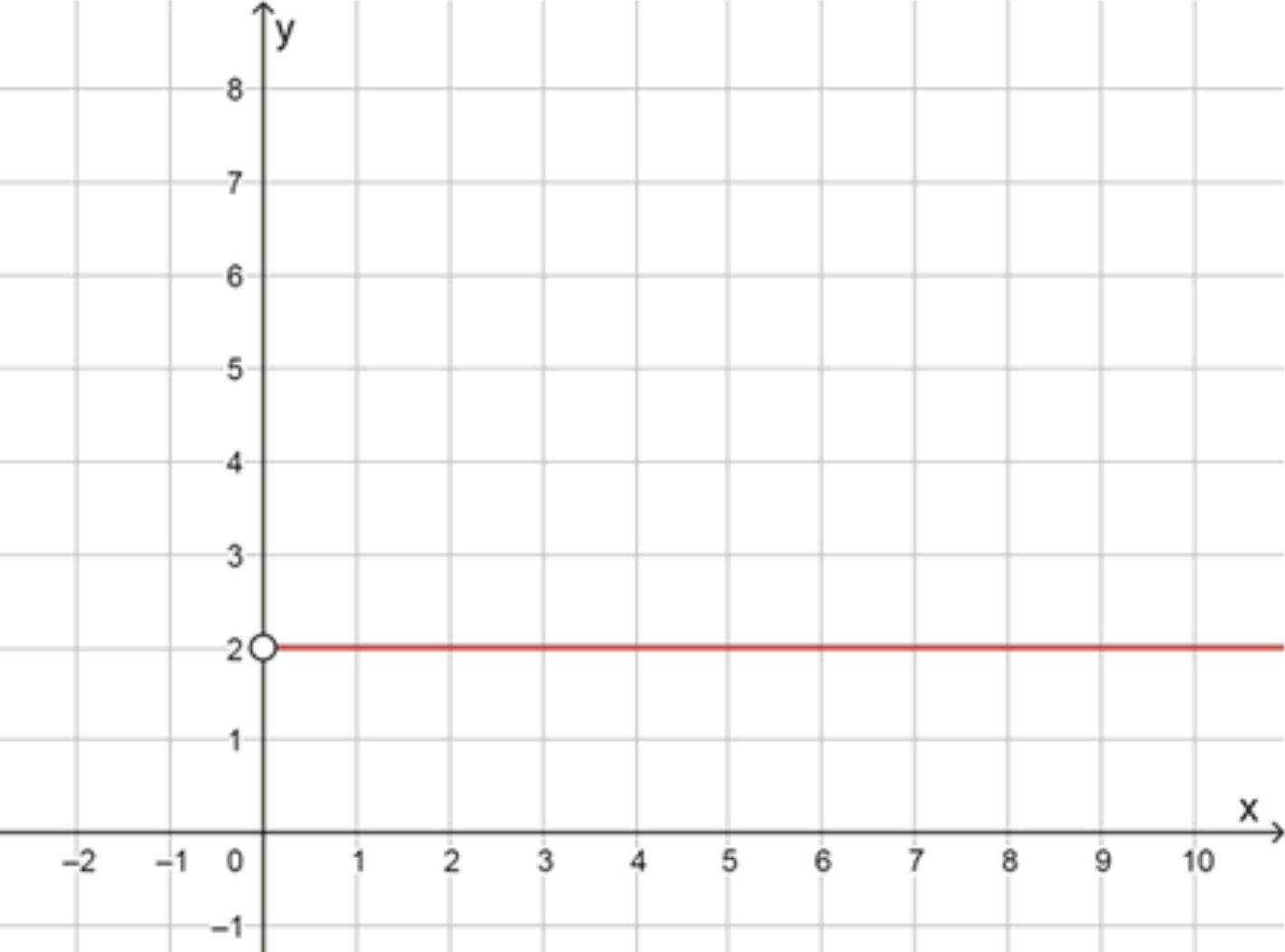
Шаг 3. Описание графика

График — горизонтальная прямая $y = 2$, при условии:

$$x > 0,\ x \ne 1$$

Особенность:
Прямая $y = 2$, но в точке $x = 1$ — разрыв (значение не определено, потому что логарифм по основанию 1 не существует).

г) $y = \log_x \frac{1}{x} = \log_x x^{-1} = -1$

Шаг 1. Область определения

• $x > 0$ — основание логарифма;
• $x \ne 1$ — логарифм по основанию 1 не определён;
• $\frac{1}{x} > 0$ — это всегда верно при $x > 0$

Итак, область определения:

$$x > 0,\ x \ne 1$$

Шаг 2. Преобразуем:

$$\log_x \frac{1}{x} = \log_x x^{-1} = -1 \cdot \log_x x = -1 \cdot 1 = -1$$

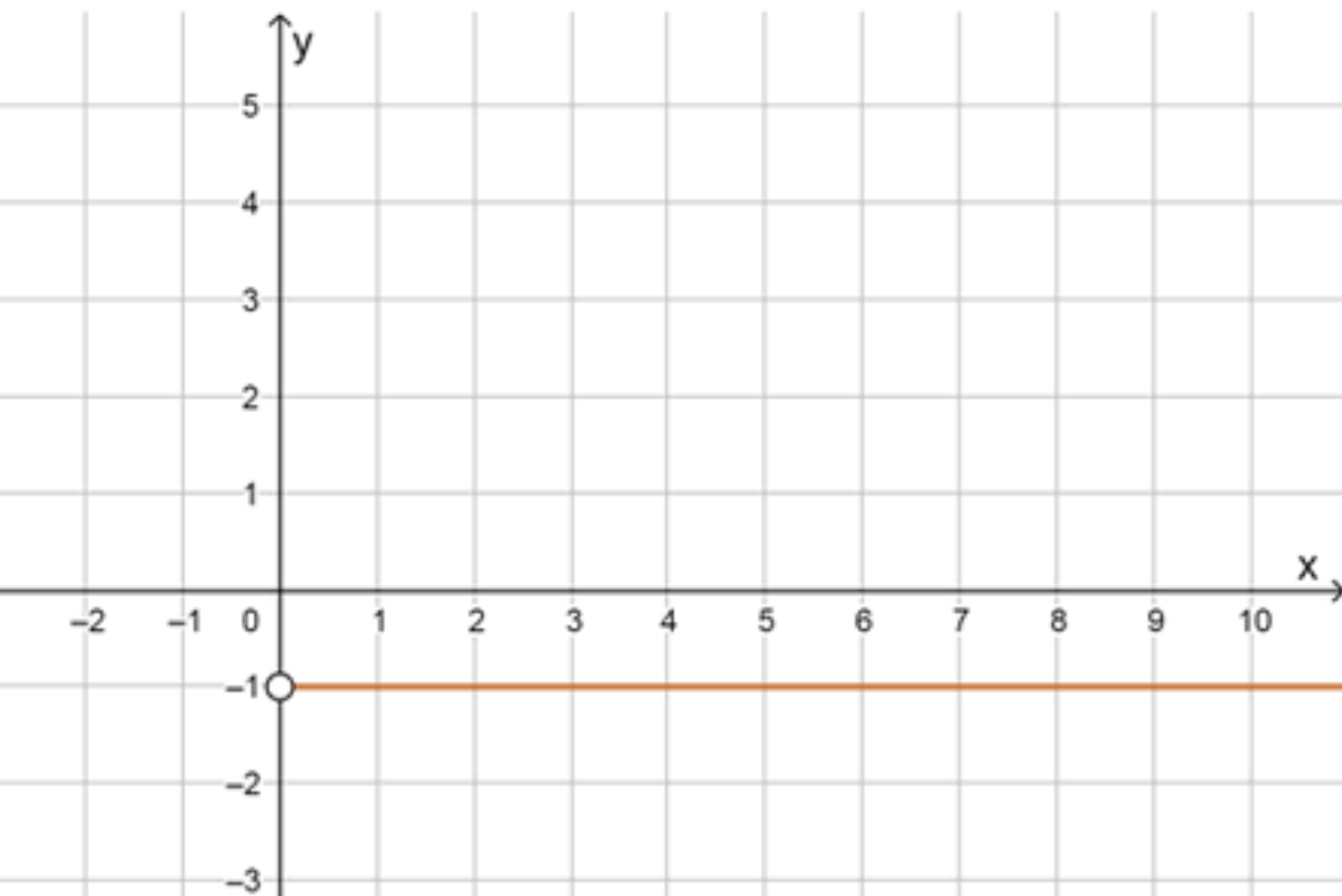
Шаг 3. Описание графика

График — горизонтальная прямая $y = -1$, но только на:

$$x > 0,\ x \ne 1$$

Особенность:
В точке $x = 1$ — разрыв (логарифм по основанию 1 не определён).
На всём остальном положительном интервале график остаётся на уровне $y = -1$.