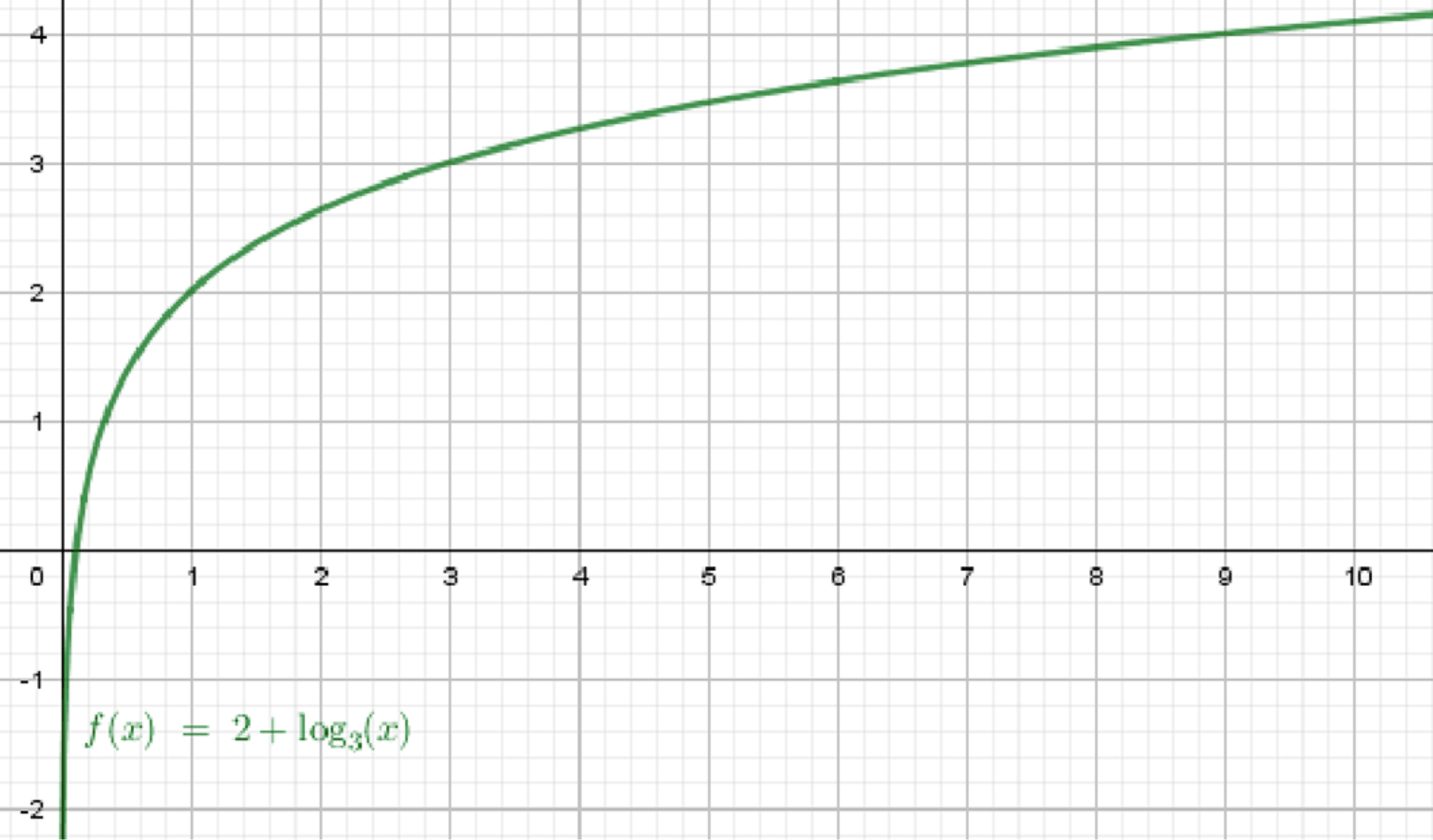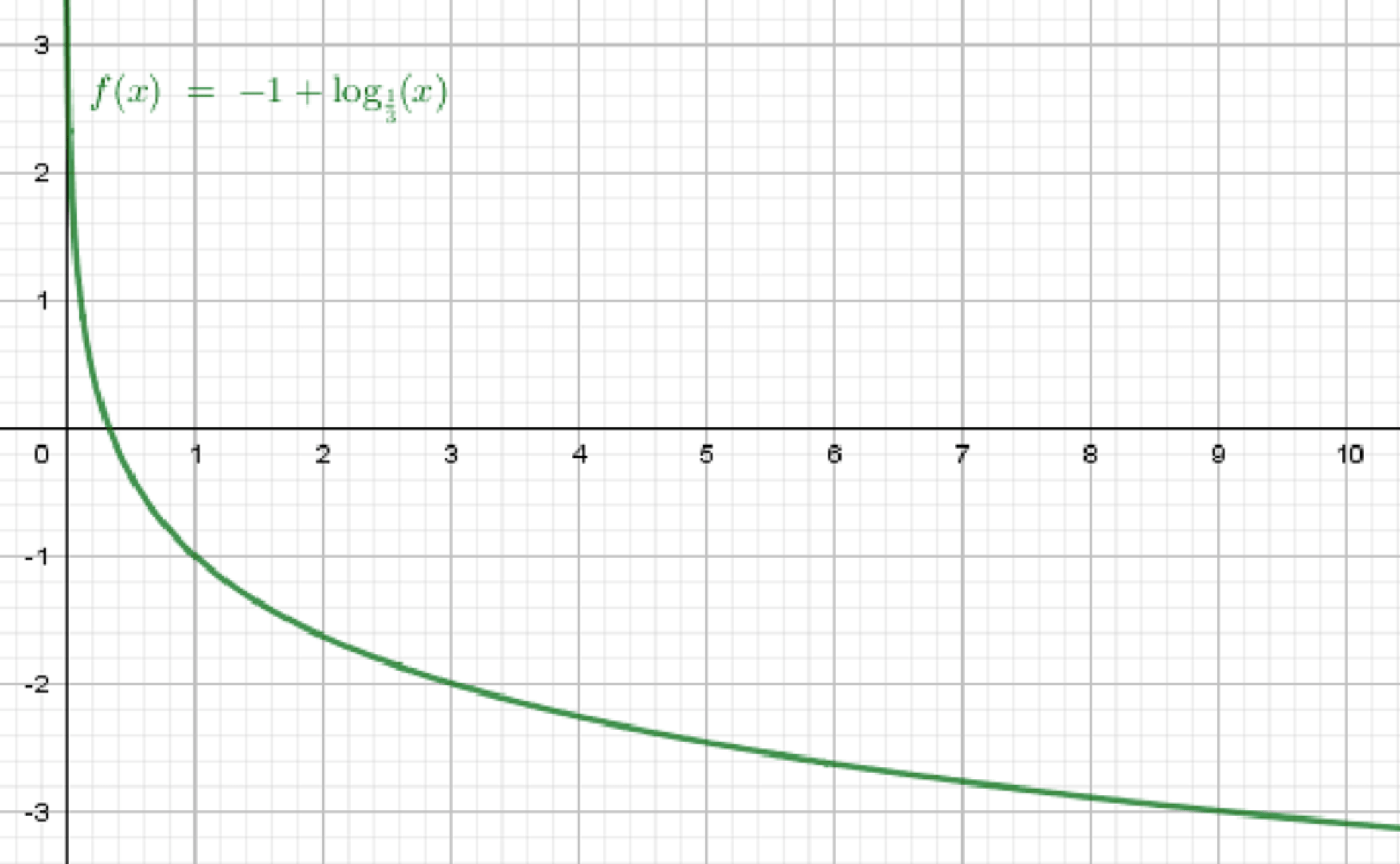ГДЗ 10-11 Класс Номер 42.11 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = 2 + \log_3 x$;

б) $y = -1 + \log_{\frac{1}{3}} x$;

в) $y = -3 + \log_4 x$;

г) $y = 0{,}5 + \log_{0{,}1} x$

Построить график функции:

а) $y = 2 + \log_3 x$;
Построим график функции $y = \log_3 x$;
Переместим его на 2 единицы вверх:

б) $y = -1 + \log_{\frac{1}{3}} x$;
Построим график функции $y = \log_{\frac{1}{3}} x$;
Переместим его на 1 единицу вниз:

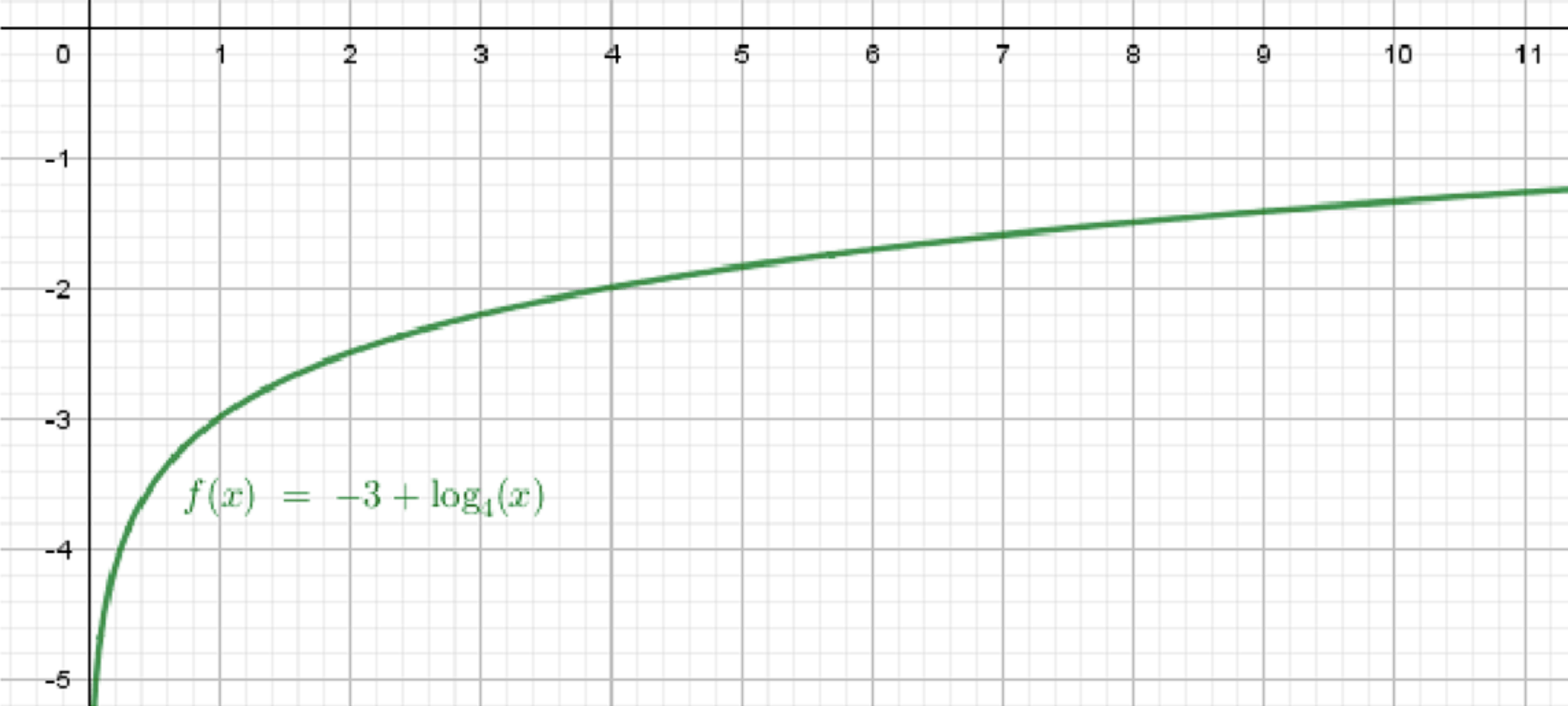
в) $y = -3 + \log_4 x$;
Построим график функции $y = \log_4 x$;
Переместим его на 3 единицы вниз:

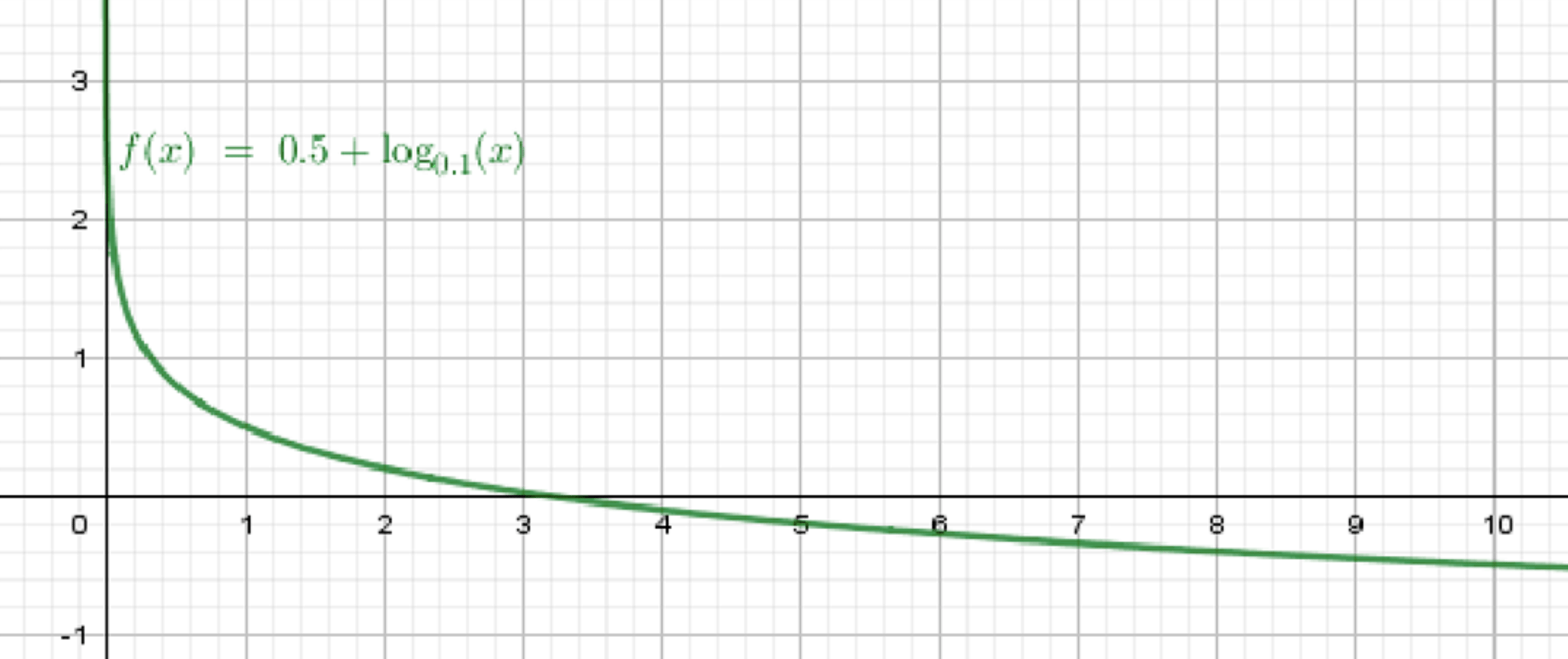
г) $y = 0{,}5 + \log_{0{,}1} x$;
Построим график функции $y = \log_{0{,}1} x$;
Переместим его на 0{,}5 единиц вверх:

а) $y = 2 + \log_3 x$

Шаг 1. Базовая функция

Рассматриваем сначала $y = \log_3 x$

• Область определения: $x > 0$
• Функция возрастает, так как основание $3 > 1$
• Вертикальная асимптота: прямая $x = 0$
• Точка на графике: $(1,\ 0)$, так как $\log_3 1 = 0$

Шаг 2. Сдвиг графика

К функции прибавлено число $+2$, значит график сдвигается вверх на 2 единицы

Шаг 3. Новый график

График функции $y = 2 + \log_3 x$:

• Область определения остаётся: $x > 0$
• Асимптота остаётся: $x = 0$
• Все значения $y$ увеличиваются на 2
• Точка $(1,\ 0)$ превращается в $(1,\ 2)$
• Функция по-прежнему возрастает

б) $y = -1 + \log_{\frac{1}{3}} x$

Шаг 1. Базовая функция

Рассматриваем $y = \log_{1/3} x$

• Основание $\frac{1}{3} < 1$, значит функция убывает
• Область определения: $x > 0$
• Асимптота: $x = 0$
• Точка $(1,\ 0)$, так как $\log_a 1 = 0$ при любом $a > 0$, $a \ne 1$

Шаг 2. Сдвиг графика

Прибавлено $-1$ — значит сдвиг вниз на 1 единицу

Шаг 3. Новый график

График функции $y = \log_{1/3} x — 1$:

• Область определения: $x > 0$
• Асимптота: $x = 0$
• Точка $(1,\ 0)$ становится $(1,\ -1)$
• Функция убывает на всём своём определении

в) $y = -3 + \log_4 x$

Шаг 1. Базовая функция

Функция $y = \log_4 x$:

• Основание $4 > 1$, значит функция возрастает
• Область определения: $x > 0$
• Асимптота: $x = 0$
• Точка $(1,\ 0)$

Шаг 2. Сдвиг вниз на 3

График сдвигается вниз на 3 единицы

Шаг 3. Новый график

График $y = \log_4 x — 3$:

• Область определения: $x > 0$
• Асимптота: остаётся $x = 0$
• Точка $(1,\ 0) \to (1,\ -3)$
• График возрастает
• Все значения функции уменьшены на 3

г) $y = 0{,}5 + \log_{0{,}1} x$

Шаг 1. Базовая функция

Функция $y = \log_{0.1} x$:

• Основание $0{,}1 < 1$, значит функция убывает
• Область определения: $x > 0$
• Асимптота: $x = 0$
• Точка $(1,\ 0)$

Шаг 2. Сдвиг вверх на 0.5

График сдвигается вверх на 0.5 единицы

Шаг 3. Новый график

График $y = \log_{0{,}1} x + 0{,}5$:

• Область определения: $x > 0$
• Асимптота: остаётся $x = 0$
• Точка $(1,\ 0) \to (1,\ 0{,}5)$
• Функция убывает