ГДЗ 10-11 Класс Номер 42.19 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x) = \begin{cases} -3x + 3, \text{ если } x \leq 1, \\ \log_{\frac{1}{3}} x, \text{ если } x > 1. \end{cases}$$

а) Вычислите $f(-8), f(-6), f(0), f(3), f(9);$

б) постройте график функции.

в) прочитайте график функции.

Дана функция:

$$f(x) = \begin{cases} -3x + 3, \text{ если } x \leq 1 \\ \log_{\frac{1}{3}} x, \text{ если } x > 1 \end{cases}$$

а) Значения функции:

$$f(-8)=-3\cdot (-8)+3=24+3=27;$$

$$f(-8) = -3 \cdot (-8) + 3 = 24 + 3 = 27;$$ $$f(-6)=-3\cdot (-6)+3=18+3=21;$$

$$f(-6) = -3 \cdot (-6) + 3 = 18 + 3 = 21;$$ $$f(0)=-3\cdot 0+3=3;$$

$$f(0) = -3 \cdot 0 + 3 = 3;$$ $$f(3)={\log }_{\frac{1}{3}}3={\log }_{\frac{1}{3}}{\left(\frac{1}{3}\right)}^{-1}=-1;$$

$$f(3) = \log_{\frac{1}{3}} 3 = \log_{\frac{1}{3}} \left(\frac{1}{3}\right)^{-1} = -1;$$ $$f(9) = \log_{\frac{1}{3}} 9 = \log_{\frac{1}{3}} \left(\frac{1}{3}\right)^{-2} = -2;$$

б) Построить график функции $y = f(x)$;

$y = -3x + 3$ — уравнение прямой:

$y = \log_{\frac{1}{3}} x$ — логарифмическая функция:

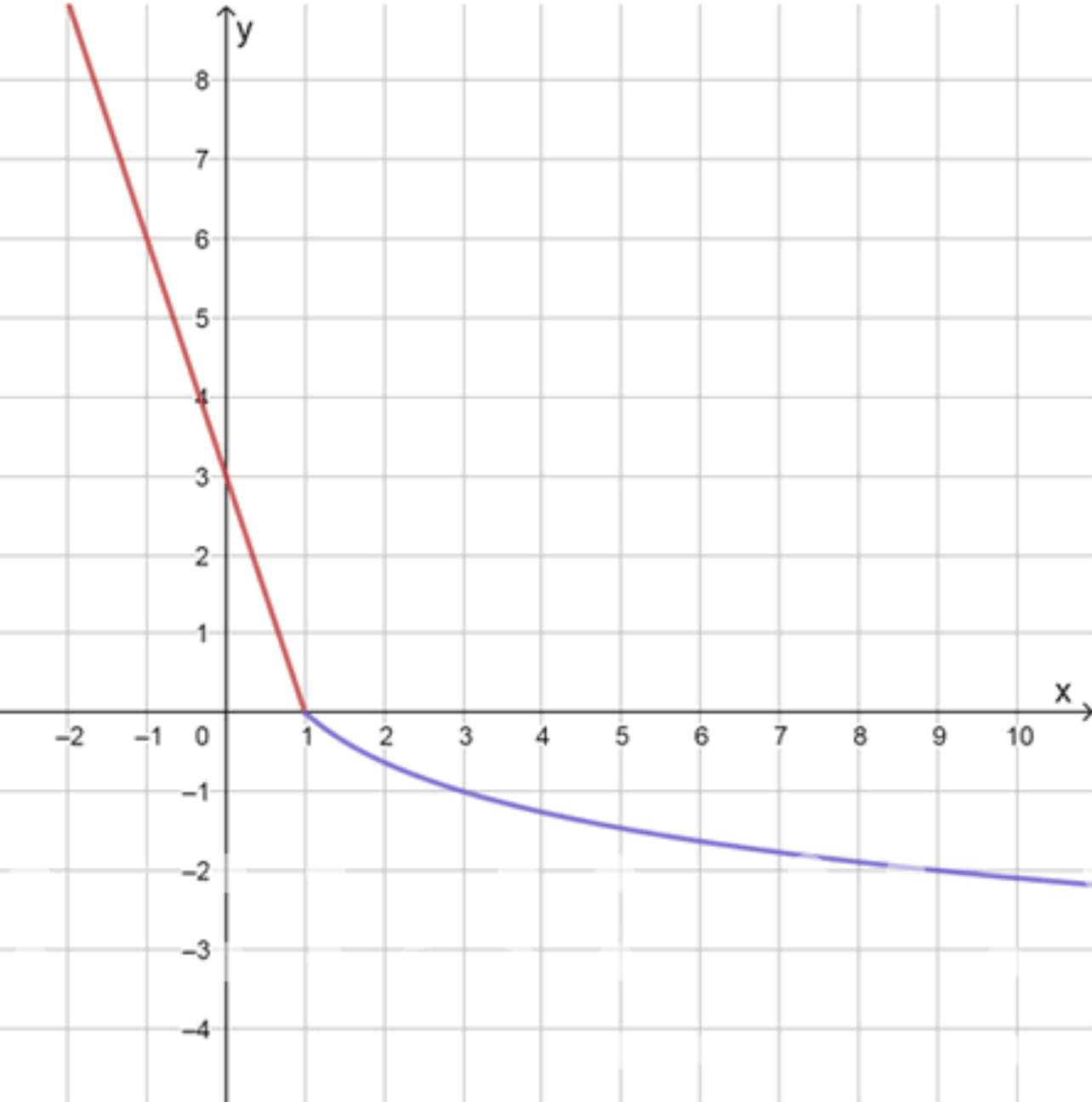
График функции:

в) Свойства функции:

$$D(f) = (-\infty; +\infty);$$

Ни чётная, ни нечётная;

Убывает на всей числовой прямой;

Не ограничена снизу, не ограничена сверху;

$y_{\text{наим}}$ — не существует, $y_{\text{наиб}}$ — не существует;

Непрерывна на всей области определения;

$$E(f) = (-\infty; +\infty);$$

Функция дифференцируема во всех точках, кроме $x = 1$.

Дана функция:

$$f(x) = \begin{cases} -3x + 3, \text{ если } x \leq 1 \\ \log_{\frac{1}{3}} x, \text{ если } x > 1 \end{cases}$$

а) Значения функции:

1. $f(-8)$:
Поскольку $-8 \leq 1$, используем первую часть определения функции:

$$f(-8) = -3 \cdot (-8) + 3 = 24 + 3 = 27$$

2. $f(-6)$:
Так как $-6 \leq 1$, также берём первую часть:

$$f(-6) = -3 \cdot (-6) + 3 = 18 + 3 = 21$$

3. $f(0)$:
Так как $0 \leq 1$, снова применяем первую часть:

$$f(0) = -3 \cdot 0 + 3 = 0 + 3 = 3$$

4. $f(3)$:
Поскольку $3 > 1$, используем вторую часть функции — логарифмическую:

$$f(3) = \log_{\frac{1}{3}} 3$$

Представим 3 как $\left(\frac{1}{3}\right)^{-1}$, тогда:

$$f(3) = \log_{\frac{1}{3}} \left( \left( \frac{1}{3} \right)^{-1} \right) = -1$$

5. $f(9)$:
Поскольку $9 > 1$, применяем логарифмическую часть:

$$f(9) = \log_{\frac{1}{3}} 9$$

Представим 9 как $\left( \frac{1}{3} \right)^{-2}$, тогда:

$$f(9) = \log_{\frac{1}{3}} \left( \left( \frac{1}{3} \right)^{-2} \right) = -2$$

б) Построить график функции $y = f(x)$:

1. Первая часть функции: $y = -3x + 3$ при $x \leq 1$:

Это уравнение прямой линии.

Угловой коэффициент: $-3$, значит прямая убывает.

Свободный член: $+3$, значит график пересекает ось $y$ в точке $(0; 3)$.

Для построения возьмём 2 точки:

Значит, отрезок графика — прямая линия, проходящая через точки $(0; 3)$ и $(1; 0)$, и продолжается влево (при $x < 1$).

Граница в точке $x = 1$ включена (так как $x \leq 1$), поэтому точка $(1; 0)$ входит в график.

2. Вторая часть функции: $y = \log_{\frac{1}{3}} x$ при $x > 1$:

Это логарифмическая функция с основанием $\frac{1}{3}$, где $0 < \frac{1}{3} < 1$, поэтому функция убывает на своём множестве определения.

Область определения: $x > 0$, но по условию — только $x > 1$.

Основные точки:

Функция стремится к $-\infty$ при $x \to +\infty$

Точка $(1; 0)$ не входит в график (так как $x > 1$), поэтому в точке $x = 1$ логарифмическая ветвь непрерывно присоединяется справа, но без включения.

в) Свойства функции:

Область определения (D(f)):
Функция определена при всех $x \in \mathbb{R}$, поскольку:

• Линейная часть работает при $x \leq 1$
• Логарифмическая часть определена при $x > 0$, но применяется только при $x > 1$, что допустимо.
  Ответ:

$$D(f) = (-\infty; +\infty)$$

Чётность/нечётность:

• Функция не симметрична относительно оси $y$ — значит, не чётная.
• Проверим нечётность: $f(-x) \ne -f(x)$ — например:
  $f(-1) = -3 \cdot (-1) + 3 = 6$, но $f(1) = 0$, а $-f(1) = 0 \ne 6$.
  Вывод: Ни чётная, ни нечётная.

Монотонность:

• Первая часть: $y = -3x + 3$ — линейная убывающая
• Вторая часть: $\log_{\frac{1}{3}} x$ — также убывающая
• Значит, функция убывает на всей числовой прямой (слева и справа от точки разрыва монотонности нет)

Ограниченность:

• Слева: $x \to -\infty$, $y \to +\infty$
• Справа: $x \to +\infty$, $y \to -\infty$
  — Значит, функция не ограничена ни сверху, ни снизу

Наименьшее и наибольшее значение:

• Нет ни минимального, ни максимального значения, так как функция не ограничена
  Ответ:
  $y_{\text{наим}}$ — не существует,
  $y_{\text{наиб}}$ — не существует

Непрерывность:

• Обе части (линейная и логарифмическая) непрерывны на своих промежутках
• Проверим в точке $x = 1$:
  • Слева: $\lim_{x \to 1^-} f(x) = -3 \cdot 1 + 3 = 0$
  • Справа: $\lim_{x \to 1^+} f(x) = \log_{\frac{1}{3}} 1 = 0$
    — Пределы совпадают, значит функция непрерывна в $x = 1$
    Вывод:
    Функция непрерывна на всей области определения

Область значений (E(f)):

• Левая часть: $-3x + 3$ при $x \leq 1$ — значения от $y \to +\infty$ до $y = 0$
• Правая часть: $\log_{\frac{1}{3}} x$ при $x > 1$ — значения от $0$ до $-\infty$
  — Совокупность значений покрывает все $\mathbb{R}$
  Ответ:

$$E(f) = (-\infty; +\infty)$$

Дифференцируемость:

• Обе части дифференцируемы на своих промежутках
• В точке $x = 1$:
  • Производная слева: $f'(x) = -3$
  • Производная справа: $f'(x) = \frac{1}{x \ln\left( \frac{1}{3} \right)} \Rightarrow f'(1) = \frac{1}{1 \cdot \ln \left( \frac{1}{3} \right)} \ne -3$
    — Производные не равны, значит в точке $x = 1$ функция не дифференцируема
    Вывод:
    Функция дифференцируема во всех точках, кроме $x = 1$