ГДЗ 10-11 Класс Номер 42.2 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте (схематично) график функции:

а) $y = \log_{\sqrt{3}} x$;

б) $y = \log_{\frac{1}{\pi}} x$;

в) $y = \lg x$;

г) $y = \log_{0,2} x$

Построить (схематично) график функции:

а) $y = \log_{\sqrt{3}} x$;
Функция монотонно возрастает:
$3 > 1$;
$\sqrt{3} > 1$;
График функции:

б) $y = \log_{\frac{1}{\pi}} x$;
Функция монотонно убывает:
$1 < \pi$;
$\frac{1}{\pi} < 1$;
График функции:

в) $y = \lg x$;
Функция монотонно возрастает:
$10 > 1$;
График функции:

г) $y = \log_{0,2} x$;
Функция монотонно убывает:
$0{,}2 < 1$;
График функции:

Общие свойства логарифмической функции $y = \log_a x$:

Область определения: $x > 0$

Функция определена только при: $a > 0, \; a \ne 1$

Монотонность:

• Если $a > 1$, функция возрастает.
• Если $0 < a < 1$, функция убывает.

График проходит через точку $(1, 0)$, потому что $\log_a 1 = 0$ для любого допустимого $a$.

Функция непрерывна и дифференцируема на $(0, +\infty)$.

При $x \to 0^+$, $y \to -\infty$; при $x \to +\infty$, $y \to +\infty$ или $y \to -\infty$ в зависимости от основания.

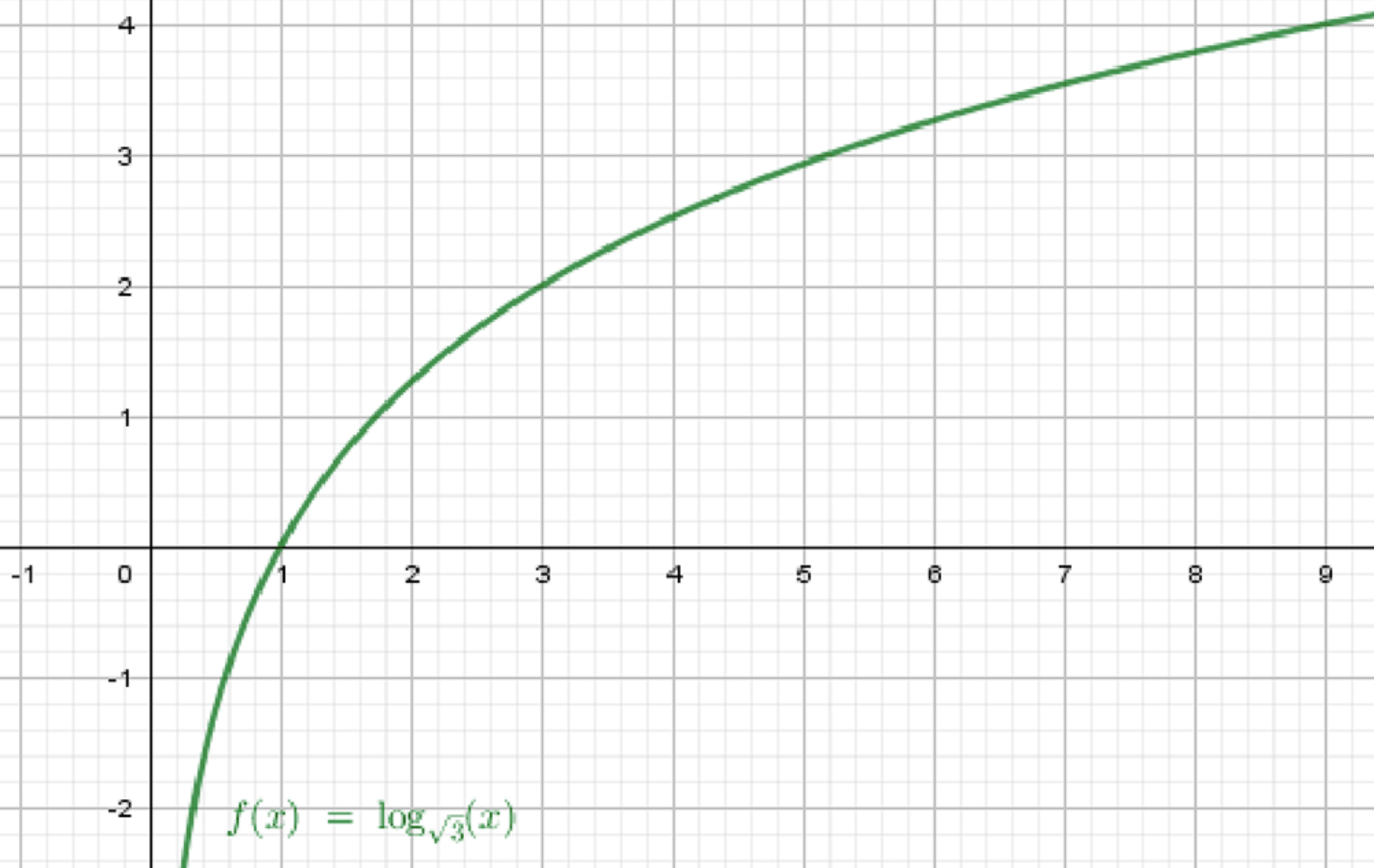
а) $y = \log_{\sqrt{3}} x$

Шаг 1. Проверим основание:

• $\sqrt{3} \approx 1{,}732$
• $\sqrt{3} > 1$ ⇒ основание больше 1
• Следовательно, функция монотонно возрастает

Шаг 2. Область определения:

• Логарифм определён только при $x > 0$

Шаг 3. Ключевые точки:

• $x = 1 \Rightarrow y = \log_{\sqrt{3}} 1 = 0$
• $x = \sqrt{3} \Rightarrow y = 1$
• $x = \frac{1}{\sqrt{3}} \Rightarrow y = -1$

Шаг 4. Поведение:

• При $x \to 0^+$, $y \to -\infty$
• При $x \to +\infty$, $y \to +\infty$

Словесное описание графика:

• Начинается от минус бесконечности по оси $y$, при $x \to 0^+$
• Монотонно возрастает
• Проходит через точку $(1, 0)$
• Чем больше $x$, тем больше $y$

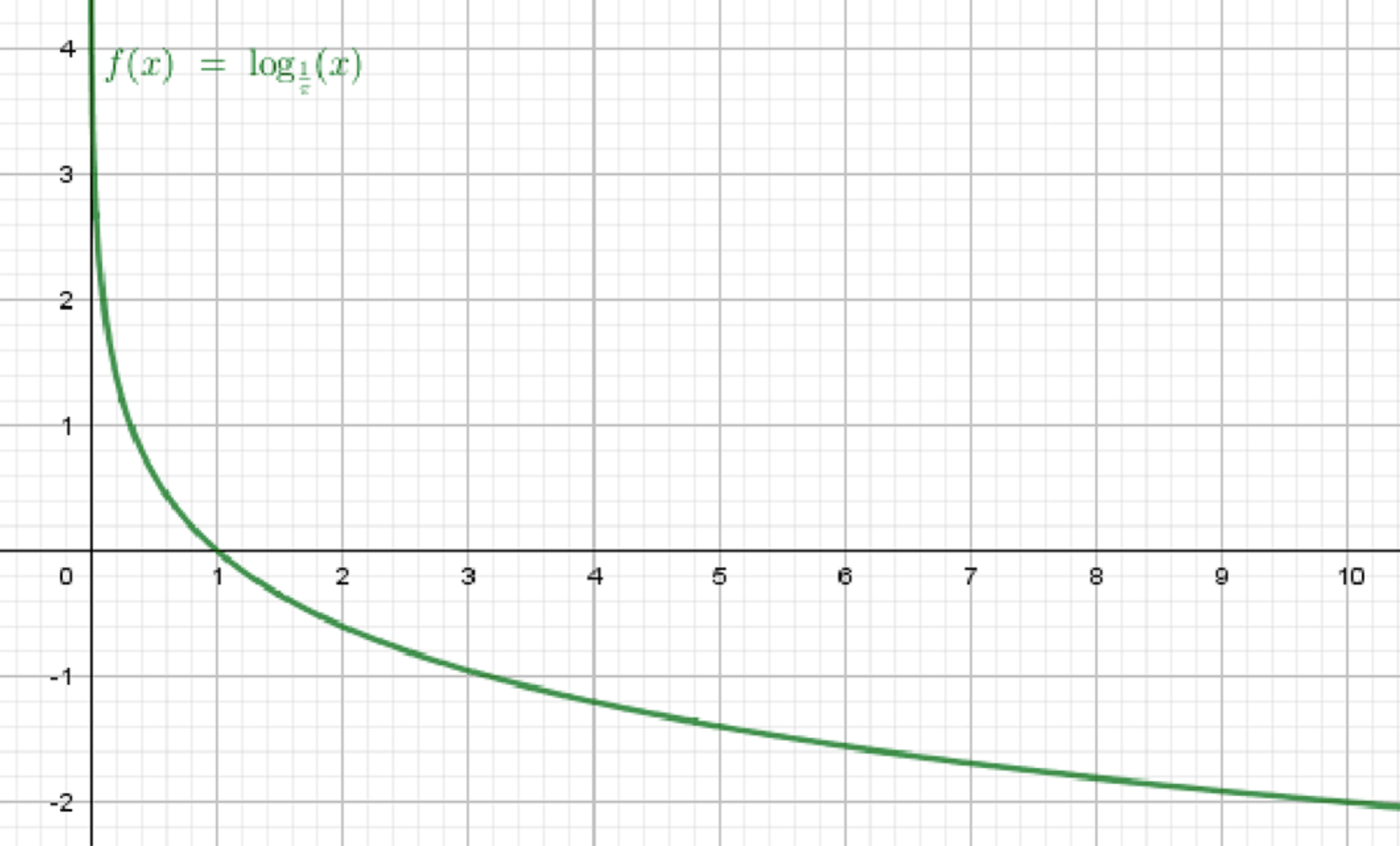
б) $y = \log_{\frac{1}{\pi}} x$

Шаг 1. Проверим основание:

• $\pi \approx 3{,}14$
• $\frac{1}{\pi} \approx 0{,}318$
• $\frac{1}{\pi} < 1$ ⇒ основание в интервале $(0, 1)$
• Следовательно, функция монотонно убывает

Шаг 2. Область определения:

• $x > 0$

Шаг 3. Ключевые точки:

• $x = 1 \Rightarrow y = \log_{1/\pi} 1 = 0$
• $x = \frac{1}{\pi} \Rightarrow y = 1$
• $x = \pi \Rightarrow y = -1$

Шаг 4. Поведение:

• При $x \to 0^+$, $y \to +\infty$
• При $x \to +\infty$, $y \to -\infty$

Словесное описание графика:

• Идёт сверху вниз
• Убывает от $+\infty$ до $-\infty$
• Проходит через точку $(1, 0)$
• Чем больше $x$, тем меньше $y$

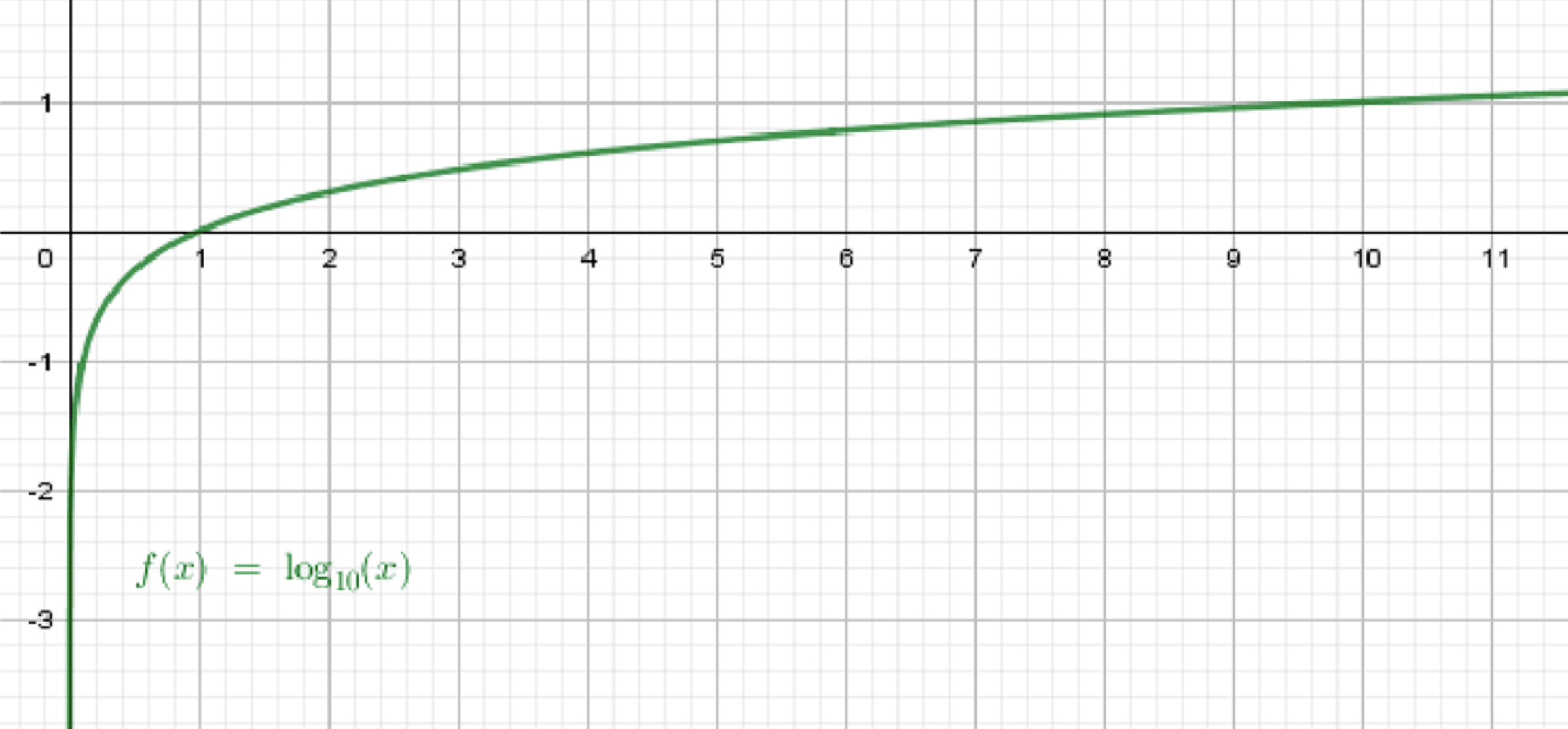
в) $y = \lg x$

Шаг 1. Это логарифм по основанию 10:

• $y = \lg x = \log_{10} x$
• Основание 10 больше 1 ⇒ функция монотонно возрастает

Шаг 2. Область определения:

• $x > 0$

Шаг 3. Ключевые точки:

• $x = 1 \Rightarrow y = \lg 1 = 0$
• $x = 10 \Rightarrow y = \lg 10 = 1$
• $x = 100 \Rightarrow y = \lg 100 = 2$
• $x = 0{,}1 \Rightarrow y = \lg 0{,}1 = -1$

Шаг 4. Поведение:

• При $x \to 0^+$, $y \to -\infty$
• При $x \to +\infty$, $y \to +\infty$

Словесное описание графика:

• Монотонно возрастает на $(0, +\infty)$
• Идёт снизу вверх
• Проходит через точку $(1, 0)$
• Имеет горизонтальный изгиб (растёт медленно при больших $x$)

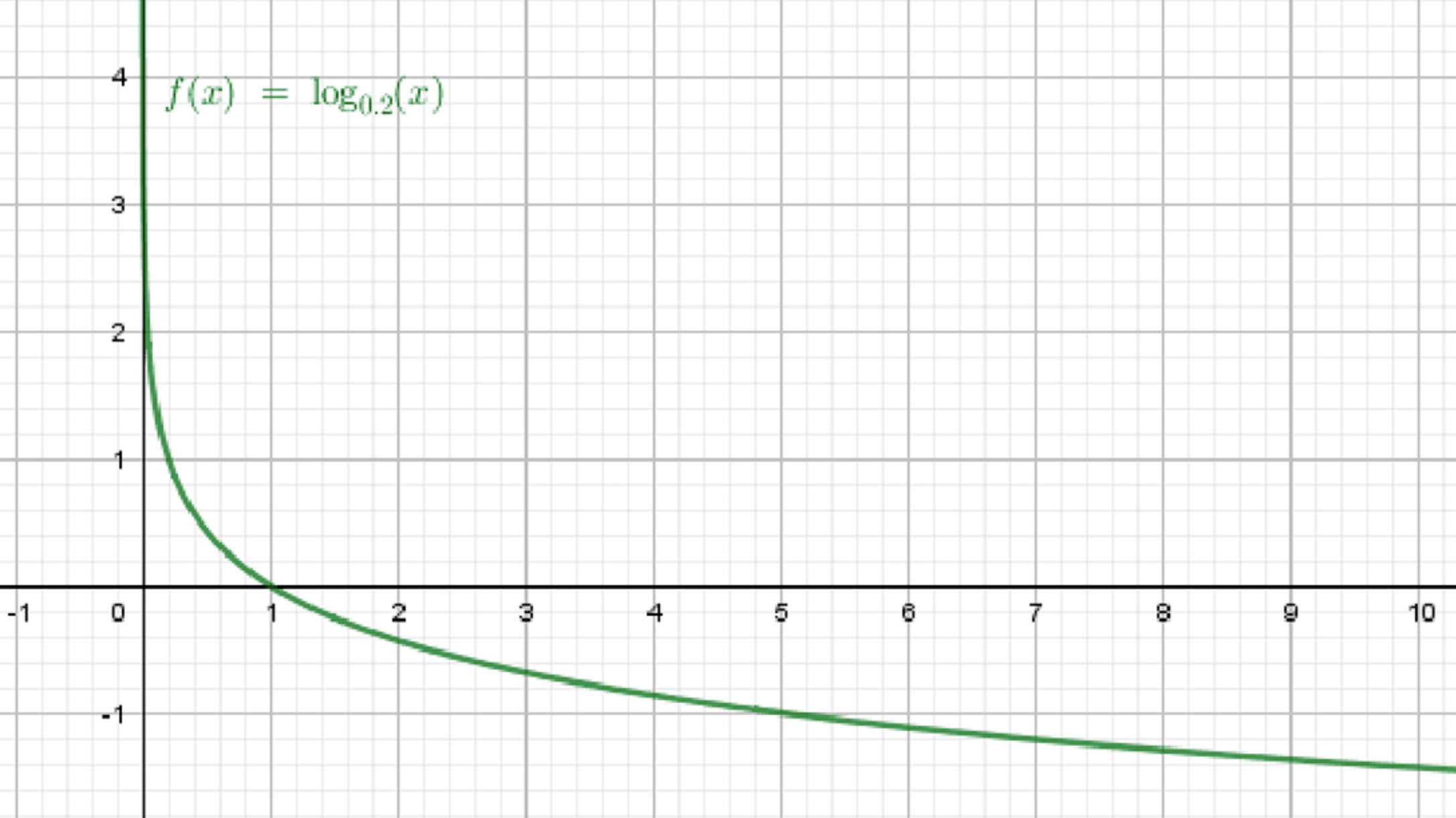
г) $y = \log_{0{,}2} x$

Шаг 1. Проверим основание:

• $0{,}2 < 1$, но $0{,}2 > 0$ ⇒ допустимое основание
• Основание в интервале $(0, 1)$ ⇒ функция монотонно убывает

Шаг 2. Область определения:

• $x > 0$

Шаг 3. Ключевые точки:

• $x = 1 \Rightarrow y = \log_{0{,}2} 1 = 0$
• $x = 0{,}2 \Rightarrow y = 1$
• $x = 5 \Rightarrow y < 0$

Дополнительно:

$$\log_{0{,}2} x = \frac{\log_{10} x}{\log_{10} 0{,}2}$$

Знаменатель отрицательный ⇒ знак логарифма меняется ⇒ функция убывает

Шаг 4. Поведение:

• При $x \to 0^+$, $y \to +\infty$
• При $x \to +\infty$, $y \to -\infty$

Словесное описание графика:

• Монотонно убывает
• Идёт сверху вниз
• Проходит через точку $(1, 0)$
• Чем больше $x$, тем меньше $y$