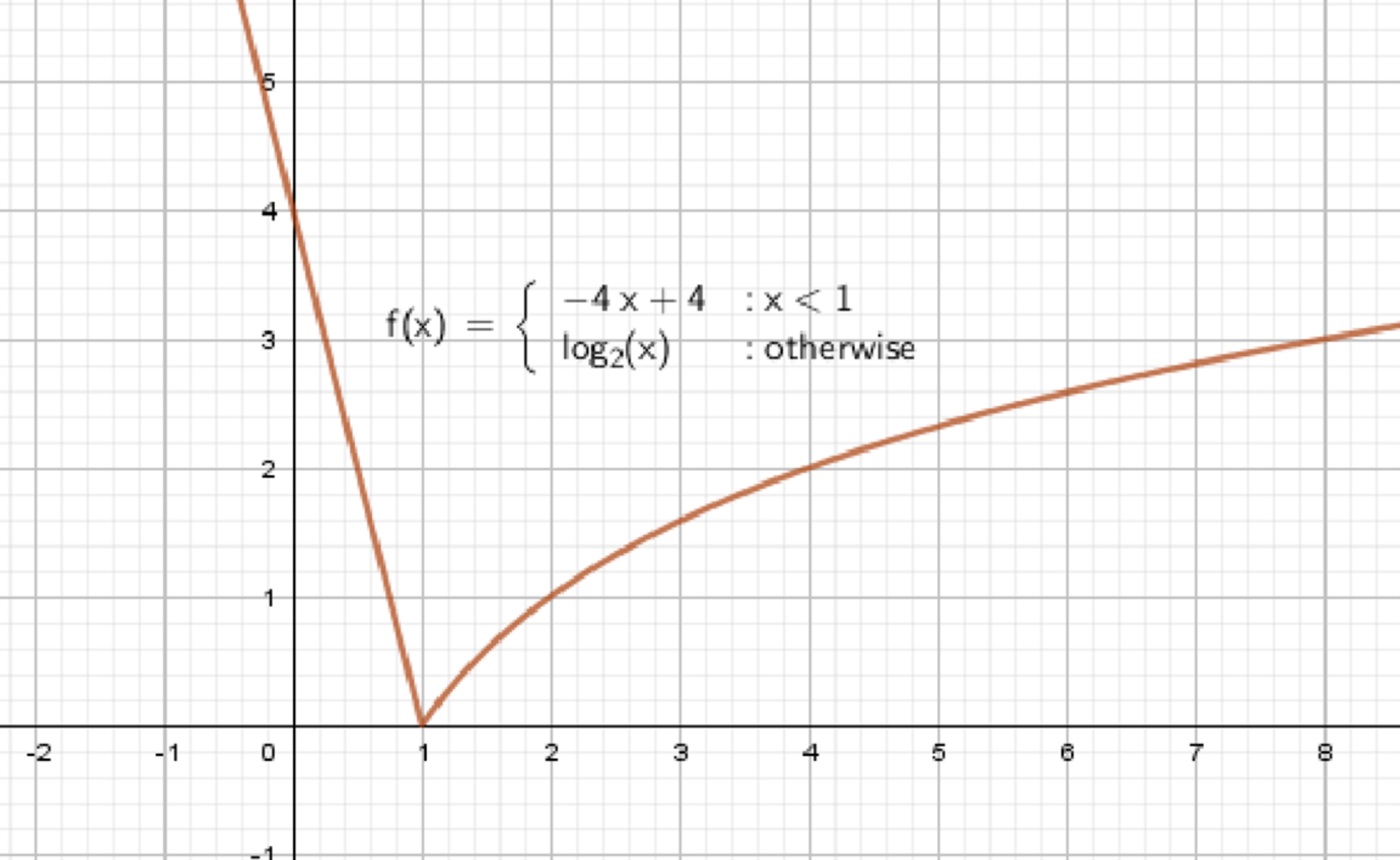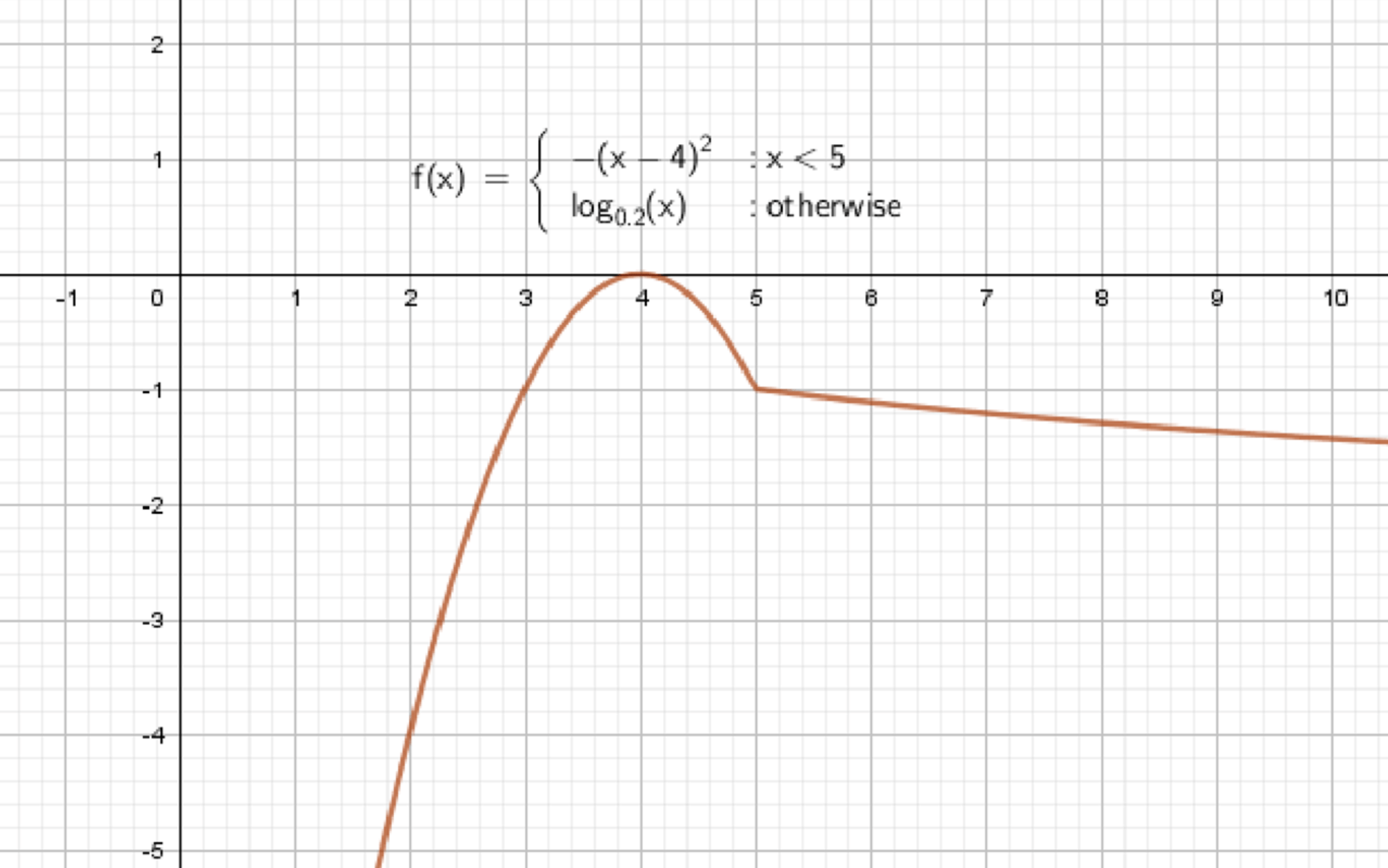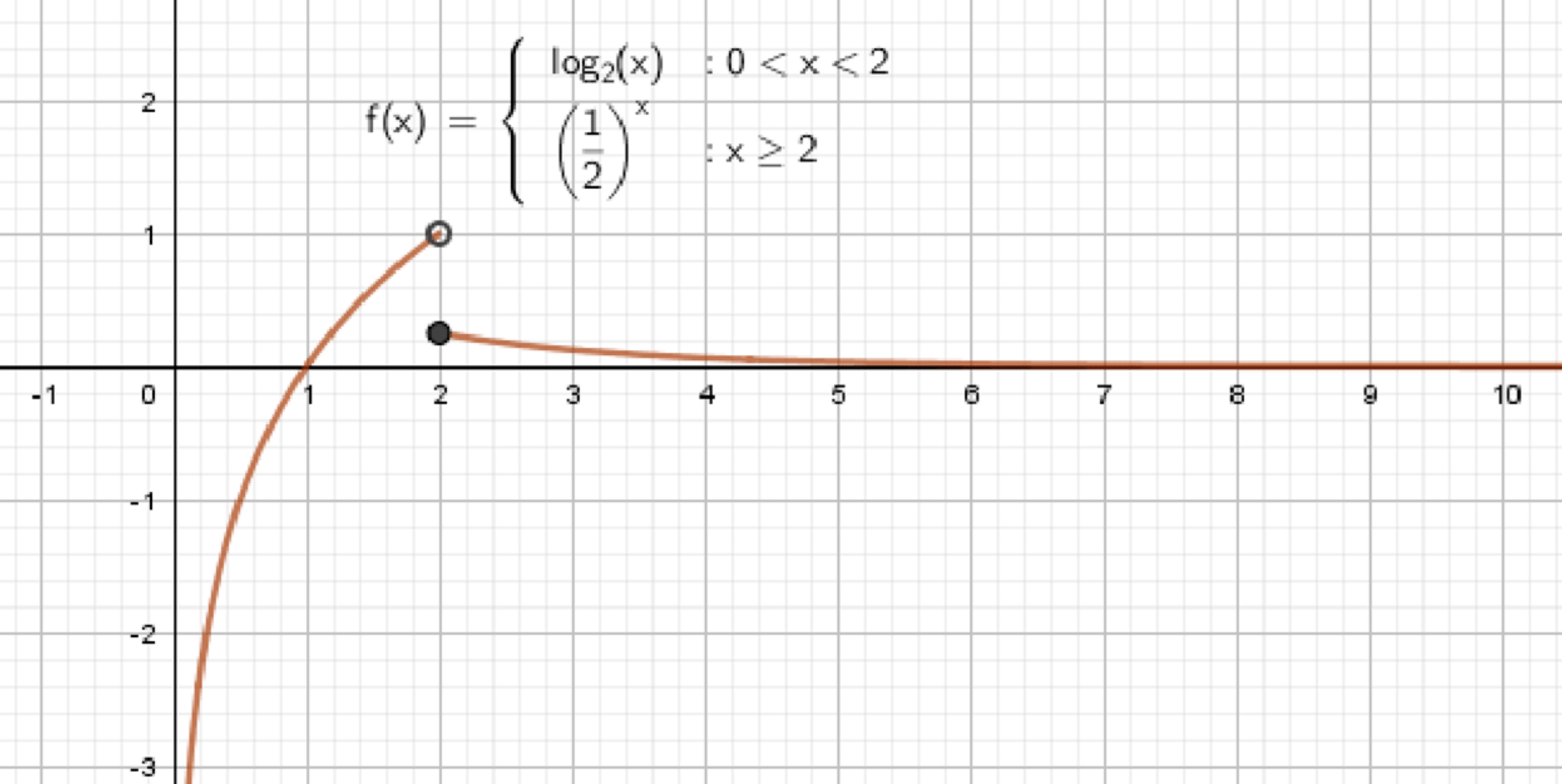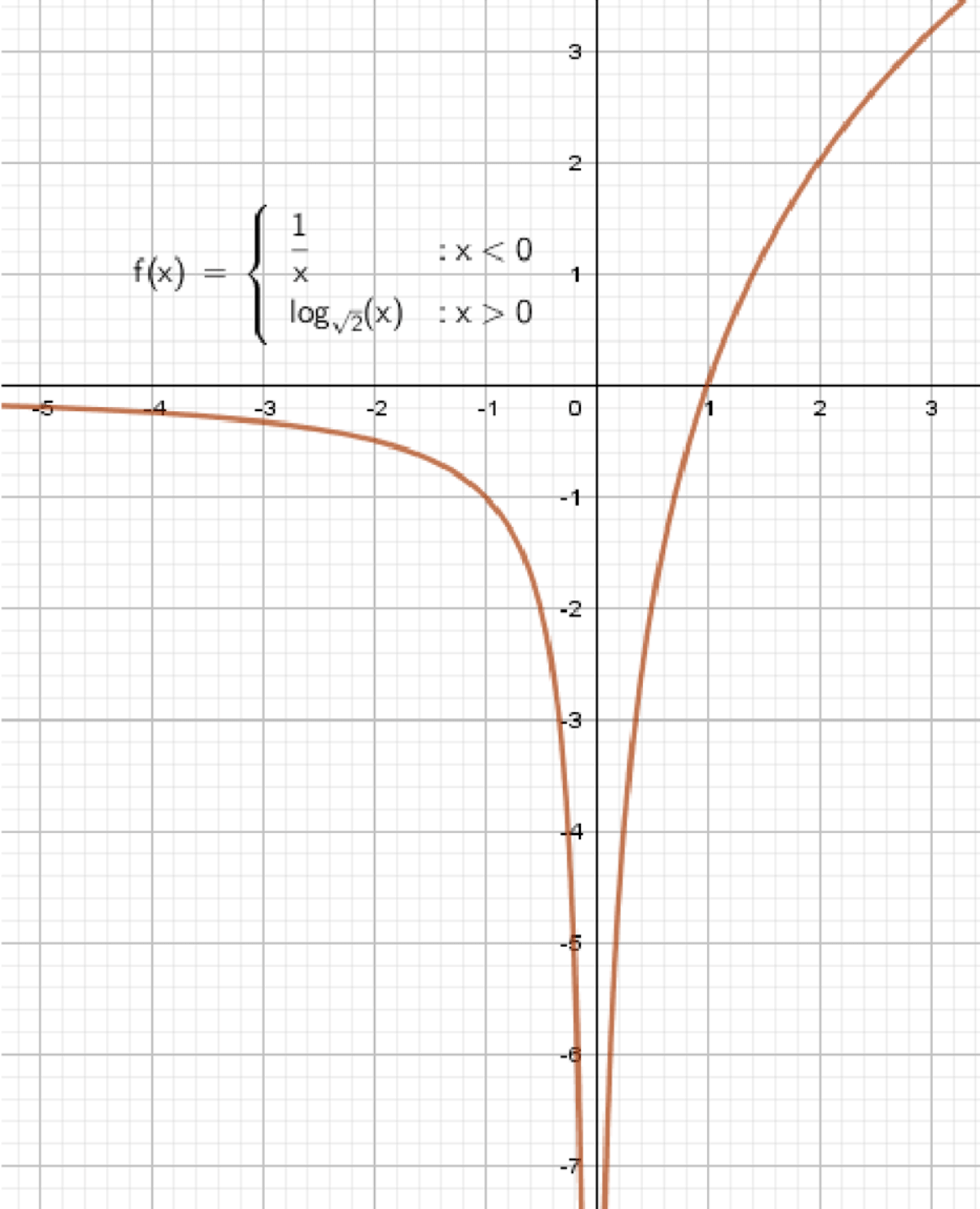ГДЗ 10-11 Класс Номер 42.20 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

а)

$$y = \begin{cases} -4x + 4, & \text{если } x < 1 \\ \log_2 x, & \text{если } x \geq 1 \end{cases}$$

б)

$$y = \begin{cases} -(x — 4)^2, & \text{если } x < 5 \\ \log_{0.2} x, & \text{если } x \geq 5 \end{cases}$$

в)

$$y = \begin{cases} \log_2 x, & \text{если } 0 < x < 2 \\ \left(\frac{1}{2}\right)^x, & \text{если } x \geq 2 \end{cases}$$

г)

$$y=\{\begin{array}{ll}\frac{1}{x},& \text{если }x<0\\ {\log }_{\sqrt{2}}x,& \text{если }x>0\end{array}$$

Построить и прочитать график функции:

а)

$$y = \begin{cases} -4x + 4, & \text{если } x < 1 \\ \log_2 x, & \text{если } x \geq 1 \end{cases}$$

1) $y = -4x + 4$ – уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 4 & 0 \\ \hline \end{array}$$

2) $y = \log_2 x$ – логарифмическая функция:

$$\begin{array}{|c|c|c|c|c|} \hline x & 1 & 2 & 4 & 8 \\ \hline y & 0 & 1 & 2 & 3 \\ \hline \end{array}$$

3) Графики функций:

4) Свойства функции:

• $D(f) = (-\infty; +\infty)$;
• Ни чётная, ни нечётная;
• Возрастает на луче $[1; +\infty)$ и убывает на луче $(-\infty; 1)$;
• Ограничена снизу, не ограничена сверху;
• $y_{\text{наим}} = 0$, $y_{\text{наиб}}$ – не существует;
• Непрерывна на всей области определения;
• $E(f) = [0; +\infty)$;
• Функция дифференцируема во всех точках, кроме $x = 1$;

б)

$$y = \begin{cases} -(x — 4)^2, & \text{если } x < 5 \\ \log_{0.2} x, & \text{если } x \geq 5 \end{cases}$$

1) $y = -(x — 4)^2$ – уравнение параболы:
Вершина: $x_0 = 4$, $y_0 = 0$;

$$\begin{array}{|c|c|c|c|c|} \hline x & 1 & 2 & 3 & 5 \\ \hline y & -9 & -4 & -1 & -1 \\ \hline \end{array}$$

2) $y = \log_{0.2} x$ – логарифмическая функция:

$$\begin{array}{|c|c|c|} \hline x & 5 & 25 \\ \hline y & -1 & -2 \\ \hline \end{array}$$

3) Графики функций:

4) Свойства функции:

• $D(f) = (-\infty; +\infty)$;
• Ни чётная, ни нечётная;
• Возрастает на луче $(-\infty; 4]$ и убывает на луче $[4; +\infty)$;
• Не ограничена снизу, ограничена сверху;
• $y_{\text{наим}}$ – не существует, $y_{\text{наиб}} = 0$;
• Непрерывна на всей области определения;
• $E(f) = (-\infty; 0]$;
• Функция дифференцируема во всех точках, кроме $x = 5$;

в)

$$y = \begin{cases} \log_2 x, & \text{если } 0 < x < 2 \\ \left(\frac{1}{2}\right)^x, & \text{если } x \geq 2 \end{cases}$$

1) $y = \log_2 x$ – логарифмическая функция:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 1 & 1 \\ \hline \end{array}$$

2) $y = \left(\frac{1}{2}\right)^x$ – показательная функция:

$$\begin{array}{|c|c|c|} \hline x & 2 & 3 \\ \hline y & 0{,}25 & 0{,}125 \\ \hline \end{array}$$

3) Графики функций:

4) Свойства функции:

• $D(f) = (0; +\infty)$;
• Ни чётная, ни нечётная;
• Возрастает на интервале $(0; 2)$, убывает на луче $[2; +\infty)$;
• Имеет горизонтальную асимптоту: $\lim\limits_{x \to +\infty} f(x) = 0$;
• Имеет вертикальную асимптоту: $x = 0$;
• Не ограничена снизу, ограничена сверху;
• $y_{\text{наим}}$ – не существует, $y_{\text{наиб}}$ – не существует;
• Непрерывна на интервалах $(0; 2) \cup (2; +\infty)$;
• $E(f) = (-\infty; 1)$;
• Функция дифференцируема всюду, кроме точки $x = 2$;

г)

$$y = \begin{cases} \frac{1}{x}, & \text{если } x < 0 \\ \log_{\sqrt{2}} x, & \text{если } x > 0 \end{cases}$$

1) $y = \frac{1}{x}$ – уравнение гиперболы:

$$\begin{array}{|c|c|c|c|} \hline x & -2 & -1 & -0{,}5 \\ \hline y & -0{,}5 & -1 & -2 \\ \hline \end{array}$$

2) $y = \log_{\sqrt{2}} x$ – логарифмическая функция:

$$\begin{array}{|c|c|c|c|c|} \hline x & 1 & 2 & 4 & 8 \\ \hline y & 0 & 2 & 4 & 6 \\ \hline \end{array}$$

3) Графики функций:

4) Свойства функции:

• $D(f) = (-\infty; 0) \cup (0; +\infty)$;
• Ни чётная, ни нечётная;
• Возрастает на луче $(0; +\infty)$, убывает на луче $(-\infty; 0)$;
• Имеет вертикальную асимптоту: $x = 0$;
• Не ограничена снизу, не ограничена сверху;
• $y_{\text{наим}}$ – не существует, $y_{\text{наиб}}$ – не существует;
• Непрерывна на интервалах $(-\infty; 0) \cup (0; +\infty)$;
• $E(f) = (-\infty; +\infty)$;
• Функция дифференцируема всюду, кроме точки $x = 0$;

а)

Функция:

$$y = \begin{cases} -4x + 4, & \text{если } x < 1 \\ \log_2 x, & \text{если } x \geq 1 \end{cases}$$

1. Анализ первой части: $y = -4x + 4$, если $x < 1$

• Это линейная функция.
• Угловой коэффициент $-4$ → функция убывает.
• Построим значения:

$$\begin{array}{|c|c|} \hline x & y = -4x + 4 \\ \hline 0 & -4 \cdot 0 + 4 = 4 \\ 1 & -4 \cdot 1 + 4 = 0 \\ \hline \end{array}$$

• Эта часть функции определена только при $x < 1$, значит:
  • Точка $(0; 4)$ входит в график.
  • Точка $(1; 0)$ не входит, но к ней приближается слева.

2. Анализ второй части: $y = \log_2 x$, если $x \geq 1$

• Это логарифмическая функция с основанием $a = 2 > 1$.
• Функция определена при $x > 0$, но используется только при $x \geq 1$.
• Функция возрастает.
• Рассчитаем значения:

$$\begin{array}{|c|c|} \hline x & y = \log_2 x \\ \hline 1 & \log_2 1 = 0 \\ 2 & \log_2 2 = 1 \\ 4 & \log_2 4 = 2 \\ 8 & \log_2 8 = 3 \\ \hline \end{array}$$

• Точка $(1; 0)$ входит в график (начало второй части).
• Функция продолжает возрастать при $x > 1$.

3. Поведение на границе $x = 1$:

• Левая часть стремится к $0$, но не включает точку.
• Правая часть начинается с точки $(1; 0)$.

→ Значит, в точке $x = 1$ график непрерывный.

4. График функции:

• Слева от $x = 1$: убывающая прямая, обрывается около $(1; 0)$.
• Справа от $x = 1$: возрастающая логарифмическая кривая, начиная с $(1; 0)$.

5. Свойства функции:

• Область определения (D):
  Линейная часть: $x < 1$
  Логарифмическая часть: $x \geq 1$
  → В совокупности:

  $$D(f) = (-\infty; +\infty)$$

• Чётность/нечётность:
  • Нет симметрии относительно $x = 0$ → не чётная.
  • $f(-x) \ne -f(x)$ → не нечётная.
    → Функция ни чётная, ни нечётная.
• Монотонность:
  • $y = -4x + 4$ убывает на $(-\infty; 1)$
  • $y = \log_2 x$ возрастает на $[1; +\infty)$
    → Функция убывает на $(-\infty; 1)$,
    возрастает на $[1; +\infty)$.
• Ограниченность:
  • Слева $x \to -\infty$ → $y \to +\infty$
  • Справа $x \to +\infty$ → $y \to +\infty$
  • Минимум достигается в точке $x = 1$: $y = 0$
    → Ограничена снизу, не ограничена сверху.
• Наименьшее и наибольшее значения:

  $$y_{\text{наим}} = 0, \quad y_{\text{наиб}} \text{ — не существует}$$

• Непрерывность:
  • Обе части непрерывны на своих промежутках.
  • В точке $x = 1$:
    $\lim_{x \to 1^-} f(x) = 0$,
    $\lim_{x \to 1^+} f(x) = 0$,
    $f(1) = 0$
    → Функция непрерывна на всей области определения.
• Область значений (E):
  • Левая часть: значения от $y \to +\infty$ до $y \to 0$
  • Правая часть: от $y = 0$ до $+\infty$
    → Совокупность:

  $$E(f) = [0; +\infty)$$

• Дифференцируемость:
  • Линейная часть: дифференцируема
  • Логарифмическая часть: тоже
  • В точке $x = 1$:
    • Слева: $f'(x) = -4$
    • Справа: $f'(x) = \frac{1}{x \ln 2} \Rightarrow f'(1) = \frac{1}{\ln 2} \approx 1.4427$
      → Производные не совпадают
      → Функция не дифференцируема в точке $x = 1$

б)

Функция:

$$y = \begin{cases} -(x — 4)^2, & \text{если } x < 5 \\ \log_{0.2} x, & \text{если } x \geq 5 \end{cases}$$

1. Анализ первой части: $y = -(x — 4)^2$, если $x < 5$

• Это парабола, ветви вниз, сдвинутая по оси $x$ на 4 единицы вправо.
• Вершина:
  $x = 4$, тогда $y = -(4 — 4)^2 = 0$ → вершина $(4; 0)$
• Построим значения:

$$\begin{array}{|c|c|} \hline x & y = -(x — 4)^2 \\ \hline 1 & -(1 — 4)^2 = -9 \\ 2 & -(2 — 4)^2 = -4 \\ 3 & -(3 — 4)^2 = -1 \\ 5 & -(5 — 4)^2 = -1 \\ \hline \end{array}$$

• Область определения этой части — $x < 5$, поэтому:
  • Значения на $x = 1, 2, 3, 4.9$ входят.
  • Точка $x = 5$ не входит.

2. Анализ второй части: $y = \log_{0.2} x$, если $x \geq 5$

• Это логарифмическая функция с основанием $a = 0.2$, $0 < a < 1$
  → функция убывает.
• Построим значения:

$$\begin{array}{|c|c|} \hline x & y = \log_{0.2} x \\ \hline 5 & \log_{0.2} 5 = -1 \\ 25 & \log_{0.2} 25 = -2 \\ \hline \end{array}$$

• При $x \to +\infty$, $y \to -\infty$
• При $x \to 0^+$, $y \to +\infty$ (но это вне области применения)
• Значение при $x = 5$:

  $$\log_{0.2} 5 = -1$$

3. Поведение на границе $x = 5$:

• Слева: $y = -(5 — 4)^2 = -1$
• Справа: $y = \log_{0.2} 5 = -1$

→ Значения совпадают → функция непрерывна в точке $x = 5$

4. График функции:

• Слева от 5 — парабола, вершина $(4; 0)$, убывает влево, симметрична.
• Справа от 5 — убывающая логарифмическая кривая, начинается в $(5; -1)$, уходит вниз.

5. Свойства функции:

• Область определения (D):
  • Первая часть: $x < 5$
  • Вторая часть: $x \geq 5$
    → Вся числовая прямая:

  $$D(f) = (-\infty; +\infty)$$

• Чётность/нечётность:
  • Нет симметрии относительно 0
  • $f(-x) \ne f(x)$, $f(-x) \ne -f(x)$
    → Функция ни чётная, ни нечётная
• Монотонность:
  • Левая часть $y = -(x — 4)^2$ возрастает на $(-\infty; 4]$, убывает на $[4; 5)$
  • Правая часть $\log_{0.2} x$ — убывает
    → Вся функция:
    • Возрастает на $(-\infty; 4]$
    • Убывает на $[4; +\infty)$
• Ограниченность:
  • Наибольшее значение достигается в вершине параболы: $y = 0$
  • Функция не ограничена снизу (логарифм уходит в $-\infty$)
    → Ограничена сверху, не ограничена снизу
• Наименьшее и наибольшее значения:

  $$y_{\text{наиб}} = 0, \quad y_{\text{наим}} \text{ — не существует}$$

• Непрерывность:
  • Оба выражения непрерывны
  • В точке $x = 5$:
    $\lim_{x \to 5^-} f(x) = -1$,
    $\lim_{x \to 5^+} f(x) = -1$,
    $f(5) = -1$
    → Функция непрерывна на всей области определения
• Область значений (E):
  • Левая часть: от $y = -\infty$ до 0
  • Правая часть: логарифм убывает, значения от $-1 \to -\infty$
    → Вся функция:

  $$E(f) = (-\infty; 0]$$

• Дифференцируемость:
  • Парабола — дифференцируема
  • Логарифм — дифференцируем
  • В точке $x = 5$:
    • Левая производная:

      $$f'(x) = -2(x — 4) \Rightarrow f'(5^-) = -2(5 — 4) = -2$$

    • Правая производная:

      $$f'(x) = \frac{1}{x \ln(0.2)} \Rightarrow f'(5^+) = \frac{1}{5 \ln(0.2)} \approx -0.621$$

    → Производные не совпадают

→ Функция не дифференцируема в точке $x = 5$

в)

Функция:

$$y = \begin{cases} \log_2 x, & \text{если } 0 < x < 2 \\ \left( \dfrac{1}{2} \right)^x, & \text{если } x \geq 2 \end{cases}$$

1. Первая часть: $y = \log_2 x$, если $0 < x < 2$

• Это логарифмическая функция с основанием $a = 2 > 1$
• Функция определена при $x > 0$ и возрастает на своей области определения
• В данной задаче область ограничена: $0 < x < 2$

Вычислим значения функции:

$$\begin{array}{|c|c|} \hline x & y = \log_2 x \\ \hline 1 & \log_2 1 = 0 \\ 2^- & \log_2 2 = 1 \quad (\text{предельное значение}) \\ \hline \end{array}$$

• При $x \to 0^+$, $y \to -\infty$
• При $x \to 2^-$, $y \to 1$
• Значит, эта часть функции:
  • Определена на $(0; 2)$
  • Возрастает от $-\infty$ до значения, близкого к 1

2. Вторая часть: $y = \left( \frac{1}{2} \right)^x$, если $x \geq 2$

• Это показательная функция с основанием $0 < \frac{1}{2} < 1$, значит убывает
• Определена на всей $\mathbb{R}$, но в нашей задаче только на $x \geq 2$

Вычислим значения:

$$\begin{array}{|c|c|} \hline x & y = \left( \frac{1}{2} \right)^x \\ \hline 2 & \left( \frac{1}{2} \right)^2 = \frac{1}{4} = 0.25 \\ 3 & \left( \frac{1}{2} \right)^3 = \frac{1}{8} = 0.125 \\ \hline \end{array}$$

• При $x \to +\infty$, $y \to 0$
• Значение в точке перехода $x = 2$ — 0.25

3. Поведение в точке $x = 2$:

• Левая часть стремится к:

  $$\lim_{x \to 2^-} \log_2 x = \log_2 2 = 1$$

• Правая часть принимает значение:

  $$f(2) = \left( \frac{1}{2} \right)^2 = 0.25$$

• Значения разные, значит:
  • В точке $x = 2$ разрыв первого рода
  • Функция непрерывна на каждом промежутке, но разрывна в точке $x = 2$

4. График функции:

• На интервале $(0; 2)$: логарифмическая кривая, уходит в $-\infty$ при $x \to 0^+$, плавно поднимается до $y \to 1$
• На луче $[2; +\infty)$: показательная кривая, начинается с $y = 0.25$, убывает к 0
• В точке $x = 2$ наблюдается скачок вниз от 1 до 0.25 — разрыв

5. Свойства функции:

• Область определения (D):
  • Первая часть: $x \in (0; 2)$
  • Вторая часть: $x \in [2; +\infty)$
    → Совокупно:

  $$D(f) = (0; +\infty)$$

• Чётность/нечётность:
  • Не симметрична ни относительно $y$-оси, ни относительно начала координат
    → Ни чётная, ни нечётная
• Монотонность:
  • На $(0; 2)$: $\log_2 x$ — возрастает
  • На $[2; +\infty)$: $\left( \frac{1}{2} \right)^x$ — убывает
    → Функция:
    • Возрастает на $(0; 2)$
    • Убывает на $[2; +\infty)$
• Асимптоты:
  • Вертикальная: при $x \to 0^+$, $\log_2 x \to -\infty$
    → Вертикальная асимптота: $x = 0$
  • Горизонтальная: при $x \to +\infty$, $\left( \frac{1}{2} \right)^x \to 0$
    → Горизонтальная асимптота: $y = 0$
• Ограниченность:
  • Логарифм не ограничен снизу
  • Показательная часть ограничена сверху: максимум в точке $x = 2$ — $0.25$
    → Не ограничена снизу, ограничена сверху
• Наименьшее и наибольшее значения:
  • $y_{\text{наим}}$ — нет (уходит в $-\infty$)
  • $y_{\text{наиб}}$ — также нет, т. к. нет общего максимума на всём $D(f)$
• Непрерывность:
  • Функция непрерывна на каждом промежутке:
    • $(0; 2)$
    • $[2; +\infty)$
  • Но в точке $x = 2$ — разрыв
    → Непрерывна на $(0; 2) \cup (2; +\infty)$
• Область значений (E):
  • Первая часть: $\log_2 x \to (-\infty; 1)$
  • Вторая часть: $\left( \frac{1}{2} \right)^x \in (0; 0.25]$
    → Совокупность:
    • Максимум: $\log_2 x \to 1$ (недостижим, т. к. 2 не входит)
    • Минимум не существует
      → Приближённо:

  $$E(f) = (-\infty; 1)$$

• Дифференцируемость:
  • На каждом интервале функция дифференцируема
  • В точке $x = 2$:
    • Производные:
      • Слева:

        $$f'(x) = \frac{1}{x \ln 2} \Rightarrow f'(2^-) = \frac{1}{2 \ln 2}$$

      • Справа:

        $$f'(x) = -\left( \frac{1}{2} \right)^x \ln \left( \frac{1}{2} \right) = \left( \frac{1}{2} \right)^x \ln 2 \Rightarrow f'(2^+) = \frac{1}{4} \ln 2$$

    • Разные → не дифференцируема

г)

Функция:

$$y = \begin{cases} \frac{1}{x}, & \text{если } x < 0 \\ \log_{\sqrt{2}} x, & \text{если } x > 0 \end{cases}$$

1. Первая часть: $y = \dfrac{1}{x}$, если $x < 0$

• Это гипербола, определена при $x \ne 0$
• Мы рассматриваем только левую ветвь: $x < 0$
• Функция отрицательна и убывает на своём интервале
• При $x \to 0^-$, $y \to -\infty$
• При $x \to -\infty$, $y \to 0^-$

Вычислим значения:

$$\begin{array}{|c|c|} \hline x & y = \frac{1}{x} \\ \hline -2 & -0.5 \\ -1 & -1 \\ -0.5 & -2 \\ \hline \end{array}$$

2. Вторая часть: $y = \log_{\sqrt{2}} x$, если $x > 0$

• Это логарифмическая функция с основанием $\sqrt{2} > 1$
• Функция возрастает и определена при $x > 0$

Вычислим значения:

$$\begin{array}{|c|c|} \hline x & y = \log_{\sqrt{2}} x \\ \hline 1 & \log_{\sqrt{2}} 1 = 0 \\ 2 & \log_{\sqrt{2}} 2 = 2 \\ 4 & \log_{\sqrt{2}} 4 = 4 \\ 8 & \log_{\sqrt{2}} 8 = 6 \\ \hline \end{array}$$

• При $x \to 0^+$, $y \to -\infty$
• При $x \to +\infty$, $y \to +\infty$

3. Поведение в точке $x = 0$:

• Левая часть:
  $\lim_{x \to 0^-} \dfrac{1}{x} = -\infty$
• Правая часть:
  $\lim_{x \to 0^+} \log_{\sqrt{2}} x = -\infty$

→ Обе части стремятся к $-\infty$,
но с разных сторон (левая – из отрицательных, правая – из положительных значений)

→ В точке $x = 0$:

• функция не определена
• разрыв второго рода
• асимптота: вертикальная $x = 0$

4. График функции:

• Для $x < 0$:
  — ветвь гиперболы в III четверти, стремится к $-\infty$ при $x \to 0^-$
  — стремится к 0 при $x \to -\infty$
• Для $x > 0$:
  — логарифмическая кривая, стремится к $-\infty$ при $x \to 0^+$
  — возрастает до $+\infty$ при $x \to +\infty$

5. Свойства функции:

• Область определения (D):
  • Левая часть: $x < 0$
  • Правая часть: $x > 0$
    → Совокупно:

  $$D(f) = (-\infty; 0) \cup (0; +\infty)$$

• Чётность/нечётность:
  • Проверим: $f(-x) = \frac{1}{-x} = -\frac{1}{x}$
    и $f(x) = \log_{\sqrt{2}} x \ne -\frac{1}{x}$
  • Также $f(-x) \ne f(x)$
    → Функция ни чётная, ни нечётная
• Монотонность:
  • Левая часть $y = \dfrac{1}{x}$ убывает на $(-\infty; 0)$
  • Правая часть $y = \log_{\sqrt{2}} x$ возрастает на $(0; +\infty)$
    → Функция:
    • Убывает на $(-\infty; 0)$
    • Возрастает на $(0; +\infty)$
• Асимптоты:
  • Вертикальная асимптота в точке разрыва:

    $$x = 0$$

• Ограниченность:
  • Левая часть уходит в $-\infty$, но стремится к 0
  • Правая часть уходит в обе стороны:
    • $y \to -\infty$ при $x \to 0^+$
    • $y \to +\infty$ при $x \to +\infty$
      → Функция не ограничена ни сверху, ни снизу
• Наименьшее и наибольшее значения:
  → Ни минимум, ни максимум не существуют
• Непрерывность:
  • Непрерывна на $(-\infty; 0)$ и на $(0; +\infty)$
  • В точке $x = 0$ — разрыв второго рода
    → Непрерывна на интервалах, но не на всей области определения
• Область значений (E):
  • Левая часть: от $-\infty$ до 0 (не включая 0)
  • Правая часть: от $-\infty$ до $+\infty$
    → В совокупности:

  $$E(f) = (-\infty; +\infty)$$

• Дифференцируемость:
  • Оба выражения дифференцируемы на своих интервалах
  • В точке $x = 0$ — разрыв
    → Функция дифференцируема всюду, кроме $x = 0$