Краткий ответ:
Решить графически уравнение:
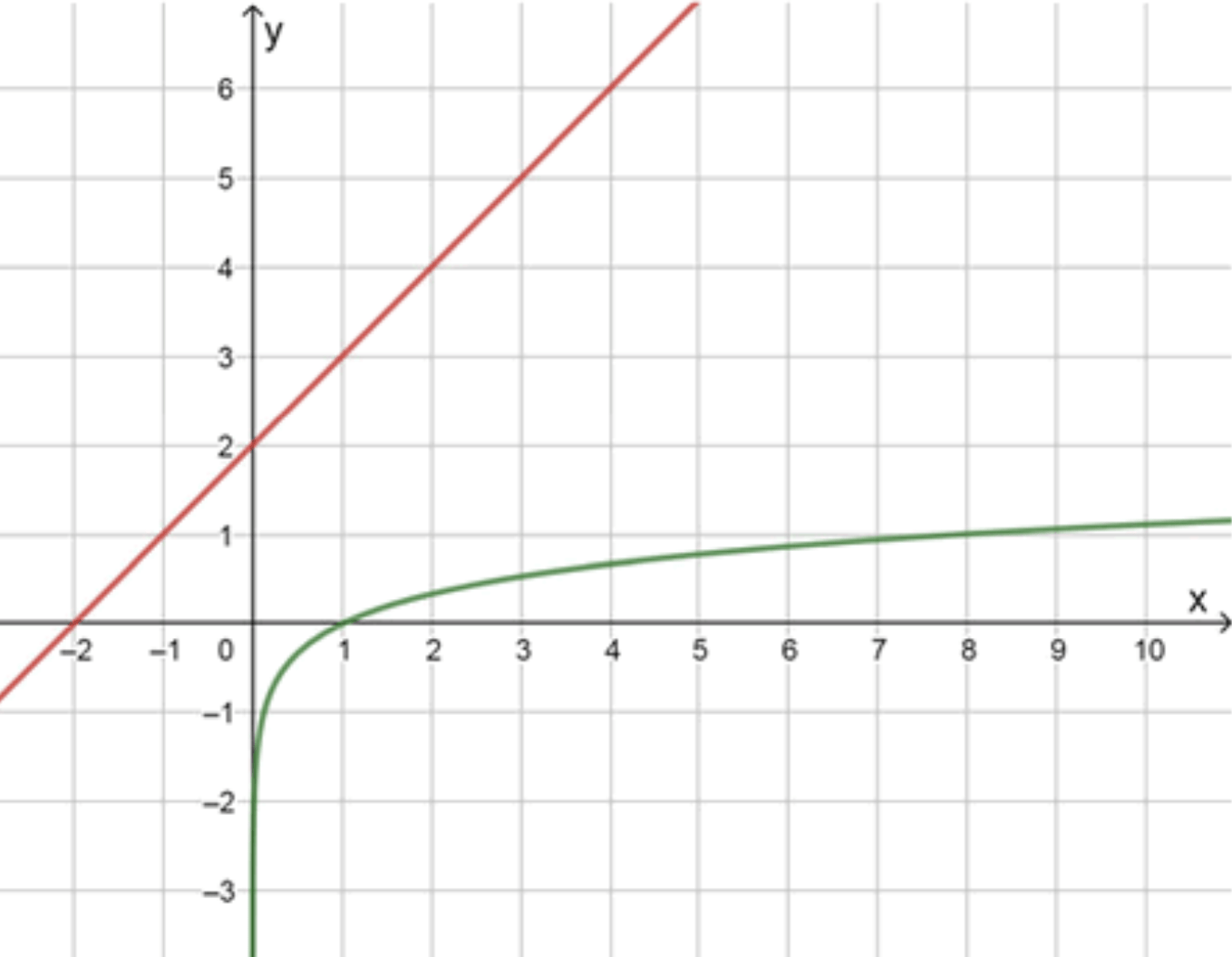
а) x + 2 = log 8 x x + 2 = \log_8 x y = log 8 x y = \log_8 x
x 1 8 y 0 1 \begin{array}{|c|c|c|} \hline x & 1 & 8 \\ \hline y & 0 & 1 \\ \hline \end{array}
y = x + 2 y = x + 2
x 0 2 y 2 4 \begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 4 \\ \hline \end{array}
Графики функций:
Ответ: нет корней.
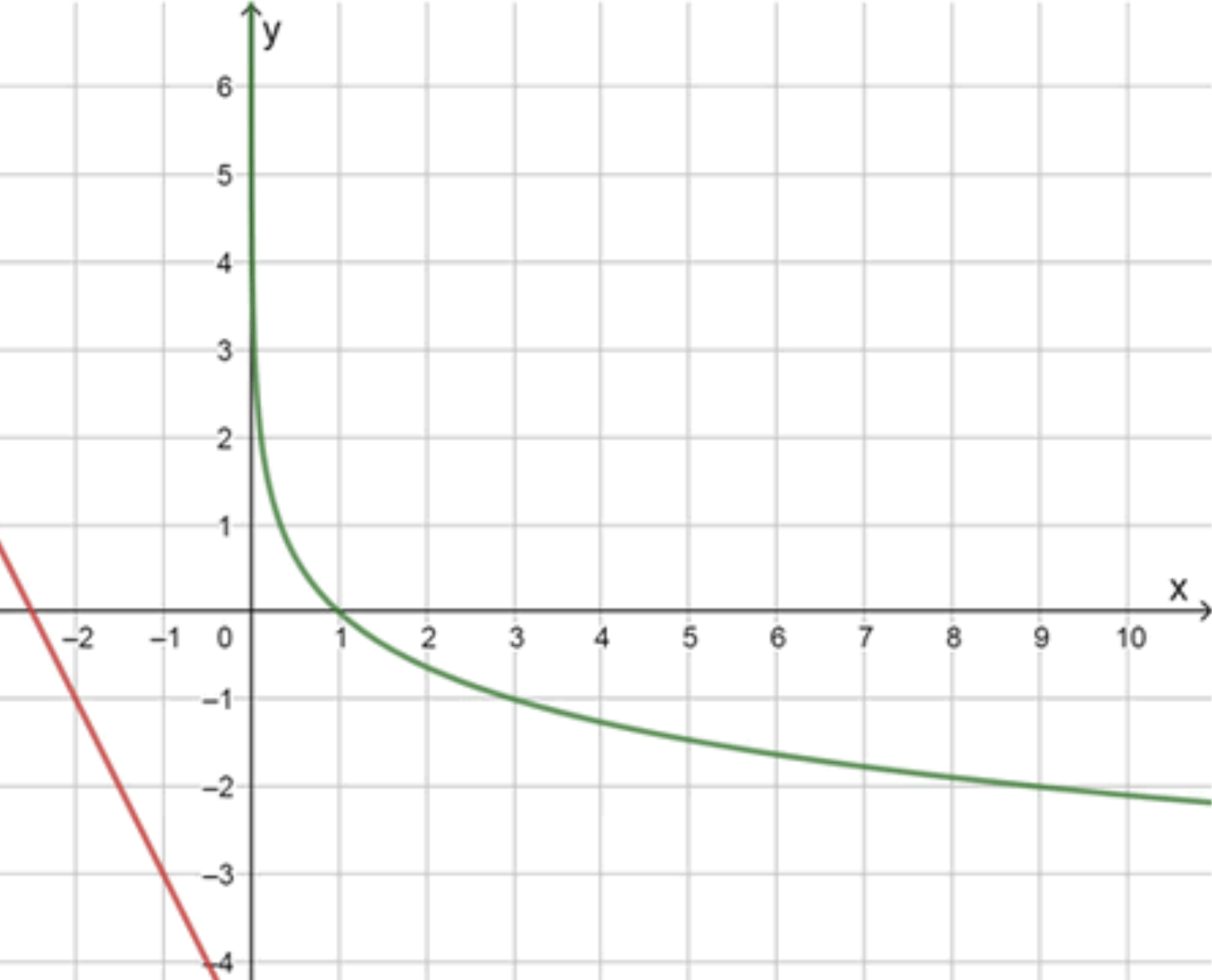
б) log 1 3 x = − 2 x − 5 \log_{\frac{1}{3}} x = -2x — 5 y = log 1 3 x y = \log_{\frac{1}{3}} x
x 1 3 9 y 0 − 1 − 2 \begin{array}{|c|c|c|c|} \hline x & 1 & 3 & 9 \\ \hline y & 0 & -1 & -2 \\ \hline \end{array}
y = − 2 x − 5 y = -2x — 5
x − 2 0 y − 1 − 5 \begin{array}{|c|c|c|} \hline x & -2 & 0 \\ \hline y & -1 & -5 \\ \hline \end{array}
Графики функций:
Ответ: нет корней.
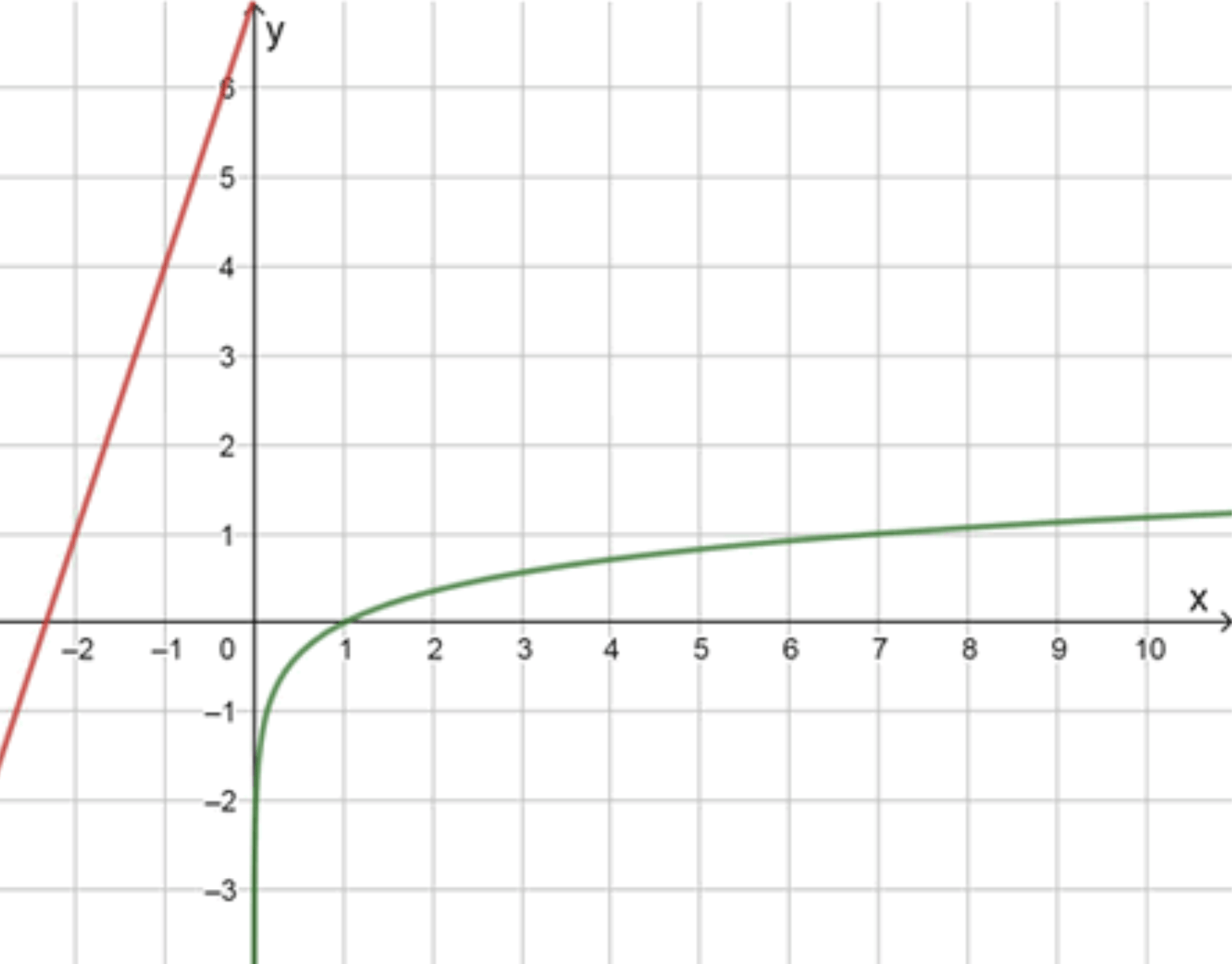
в) 3 x + 7 = log 7 x 3x + 7 = \log_7 x y = log 7 x y = \log_7 x
x 1 7 y 0 1 \begin{array}{|c|c|c|} \hline x & 1 & 7 \\ \hline y & 0 & 1 \\ \hline \end{array}
y = 3 x + 7 y = 3x + 7
x − 2 − 1 y 1 4 \begin{array}{|c|c|c|} \hline x & -2 & -1 \\ \hline y & 1 & 4 \\ \hline \end{array}
Графики функций:
Ответ: нет корней.
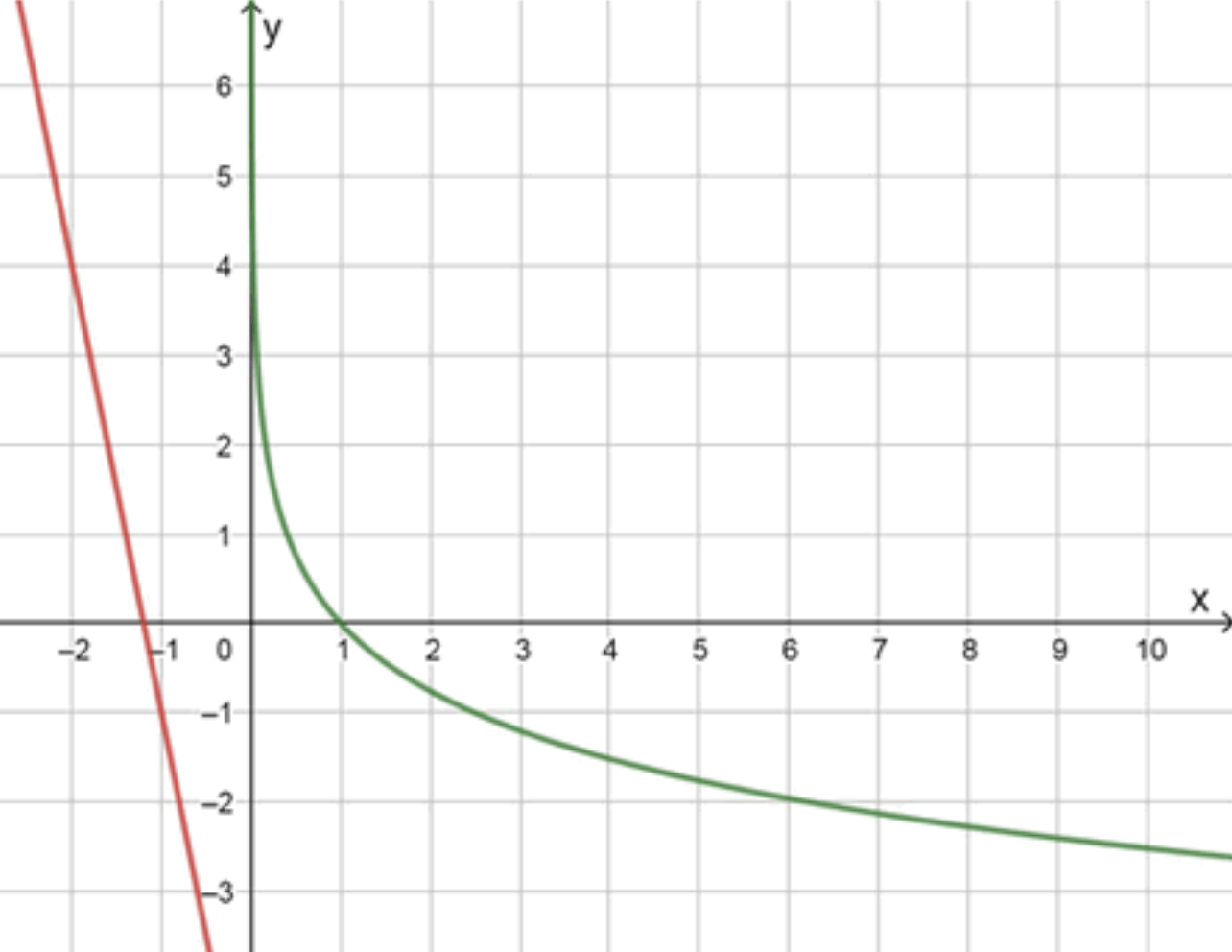
г) log 2 5 x = − 5 x − 6 \log_{\frac{2}{5}} x = -5x — 6 y = log 2 5 x y = \log_{\frac{2}{5}} x
x 1 2,5 6,25 y 0 − 1 − 2 \begin{array}{|c|c|c|c|} \hline x & 1 & 2{,}5 & 6{,}25 \\ \hline y & 0 & -1 & -2 \\ \hline \end{array}
y = − 5 x − 6 y = -5x — 6
x − 1 0 y − 1 − 6 \begin{array}{|c|c|c|} \hline x & -1 & 0 \\ \hline y & -1 & -6 \\ \hline \end{array}
Графики функций:
Ответ: нет корней.
Подробный ответ:
а) Уравнение:
x + 2 = log 8 x x + 2 = \log_8 x
Шаг 1: Область определения
Шаг 2: Построение графика y = log 8 x y = \log_8 x
Основание логарифма 8 > 1 8 > 1 возрастает на ( 0 ; + ∞ ) (0; +\infty) Характерные точки: x log 8 x 1 log 8 1 = 0 8 log 8 8 = 1 \begin{array}{|c|c|} \hline x & \log_8 x \\ \hline 1 & \log_8 1 = 0 \\ 8 & \log_8 8 = 1 \\ \hline \end{array}
Поведение:x → 0 + ⇒ y → − ∞ x \to 0^+ \Rightarrow y \to -\infty x → + ∞ ⇒ y → + ∞ x \to +\infty \Rightarrow y \to +\infty очень медленно Шаг 3: Построение графика y = x + 2 y = x + 2
Линейная функция, возрастает с угловым коэффициентом 1 1 Точки: x y 0 2 2 4 \begin{array}{|c|c|} \hline x & y \\ \hline 0 & 2 \\ 2 & 4 \\ \hline \end{array}
Прямая стремительно возрастает Шаг 4: Графический анализ
Сравним значения:При x = 1 x = 1 y = log 8 1 = 0 y = \log_8 1 = 0 y = 1 + 2 = 3 y = 1 + 2 = 3 При x = 8 x = 8 y = log 8 8 = 1 y = \log_8 8 = 1 y = 8 + 2 = 10 y = 8 + 2 = 10 → Во всех точках значение y = x + 2 y = x + 2 значительно выше , чем log 8 x \log_8 x
Шаг 5: Вывод
Логарифмическая кривая идёт ниже прямой на всём допустимом интервале Прямые не пересекаются Уравнение не имеет решений
Ответ:
нет корней \boxed{\text{нет корней}}
б) Уравнение:
log 1 3 x = − 2 x − 5 \log_{\frac{1}{3}} x = -2x — 5
Шаг 1: ОДЗ
x > 0 x > 0
Шаг 2: График y = log 1 3 x y = \log_{\frac{1}{3}} x
Основание 1 3 ∈ ( 0 ; 1 ) \frac{1}{3} \in (0; 1) убывает Характерные значения: x log 1 3 x 1 0 3 − 1 9 − 2 \begin{array}{|c|c|} \hline x & \log_{\frac{1}{3}} x \\ \hline 1 & 0 \\ 3 & -1 \\ 9 & -2 \\ \hline \end{array}
Шаг 3: График y = − 2 x − 5 y = -2x — 5
Линейная функция, убывает с угловым коэффициентом − 2 -2 Значения: x y − 2 − 1 0 − 5 \begin{array}{|c|c|} \hline x & y \\ \hline -2 & -1 \\ 0 & -5 \\ \hline \end{array}
Но на ОДЗ: x > 0 x > 0 x = 1 ⇒ y = − 2 ⋅ 1 − 5 = − 7 x = 1 \Rightarrow y = -2 \cdot 1 — 5 = -7 x = 3 ⇒ y = − 11 x = 3 \Rightarrow y = -11 Шаг 4: Сравнение значений
При x = 1 x = 1 log 1 3 1 = 0 \log_{\frac{1}{3}} 1 = 0 − 2 ( 1 ) − 5 = − 7 -2(1) — 5 = -7 При x = 3 x = 3 log 1 3 3 = − 1 \log_{\frac{1}{3}} 3 = -1 − 2 ( 3 ) − 5 = − 11 -2(3) — 5 = -11 → Логарифм выше прямой на всём x > 0 x > 0
Шаг 5: Вывод
Функции убывают, но логарифм убывает медленно, а прямая — быстро Графики не пересекаются
Ответ:
нет корней \boxed{\text{нет корней}}
в) Уравнение:
3 x + 7 = log 7 x 3x + 7 = \log_7 x
Шаг 1: ОДЗ
x > 0 x > 0
Шаг 2: График y = log 7 x y = \log_7 x
Основание 7 > 1 7 > 1 возрастает Значения: x log 7 x 1 0 7 1 \begin{array}{|c|c|} \hline x & \log_7 x \\ \hline 1 & 0 \\ 7 & 1 \\ \hline \end{array}
Шаг 3: График y = 3 x + 7 y = 3x + 7
Прямая с крутым наклоном Значения: x y − 2 1 − 1 4 0 7 \begin{array}{|c|c|} \hline x & y \\ \hline -2 & 1 \\ -1 & 4 \\ 0 & 7 \\ \hline \end{array}
Но нас интересует только x > 0 x > 0 x = 1 ⇒ y = 3 + 7 = 10 x = 1 \Rightarrow y = 3 + 7 = 10 x = 7 ⇒ y = 21 + 7 = 28 x = 7 \Rightarrow y = 21 + 7 = 28 Шаг 4: Сравнение значений
log 7 1 = 0 \log_7 1 = 0 3 ⋅ 1 + 7 = 10 3 \cdot 1 + 7 = 10 log 7 7 = 1 \log_7 7 = 1 3 ⋅ 7 + 7 = 28 3 \cdot 7 + 7 = 28 → Прямая всегда выше логарифма
Шаг 5: Вывод
Прямая и логарифм не пересекаются на допустимом интервале
Ответ:
нет корней \boxed{\text{нет корней}}
г) Уравнение:
log 2 5 x = − 5 x − 6 \log_{\frac{2}{5}} x = -5x — 6
Шаг 1: ОДЗ
x > 0 x > 0
Шаг 2: График y = log 2 5 x y = \log_{\frac{2}{5}} x
Основание 2 5 ∈ ( 0 ; 1 ) \frac{2}{5} \in (0;1) убывает Значения: x y = log 2 5 x 1 0 2.5 − 1 6.25 − 2 \begin{array}{|c|c|} \hline x & y = \log_{\frac{2}{5}} x \\ \hline 1 & 0 \\ 2.5 & -1 \\ 6.25 & -2 \\ \hline \end{array}
Шаг 3: График y = − 5 x − 6 y = -5x — 6
Линейная функция, убывает резко Значения: x y − 1 − 1 0 − 6 \begin{array}{|c|c|} \hline x & y \\ \hline -1 & -1 \\ 0 & -6 \\ \hline \end{array}
Проверим при x > 0 x > 0 x = 1 ⇒ y = − 5 − 6 = − 11 x = 1 \Rightarrow y = -5 — 6 = -11 x = 2.5 ⇒ y = − 18.5 x = 2.5 \Rightarrow y = -18.5 Шаг 4: Сравнение значений
При x = 1 x = 1 Логарифм: 0 0 Прямая: − 11 -11 При x = 2.5 x = 2.5 Логарифм: − 1 -1 Прямая: − 18.5 -18.5 → Логарифм выше прямой на всём x > 0 x > 0
Шаг 5: Вывод
Функции убывают, но прямая убывает быстрее Нет точек пересечения
Ответ:
нет корней