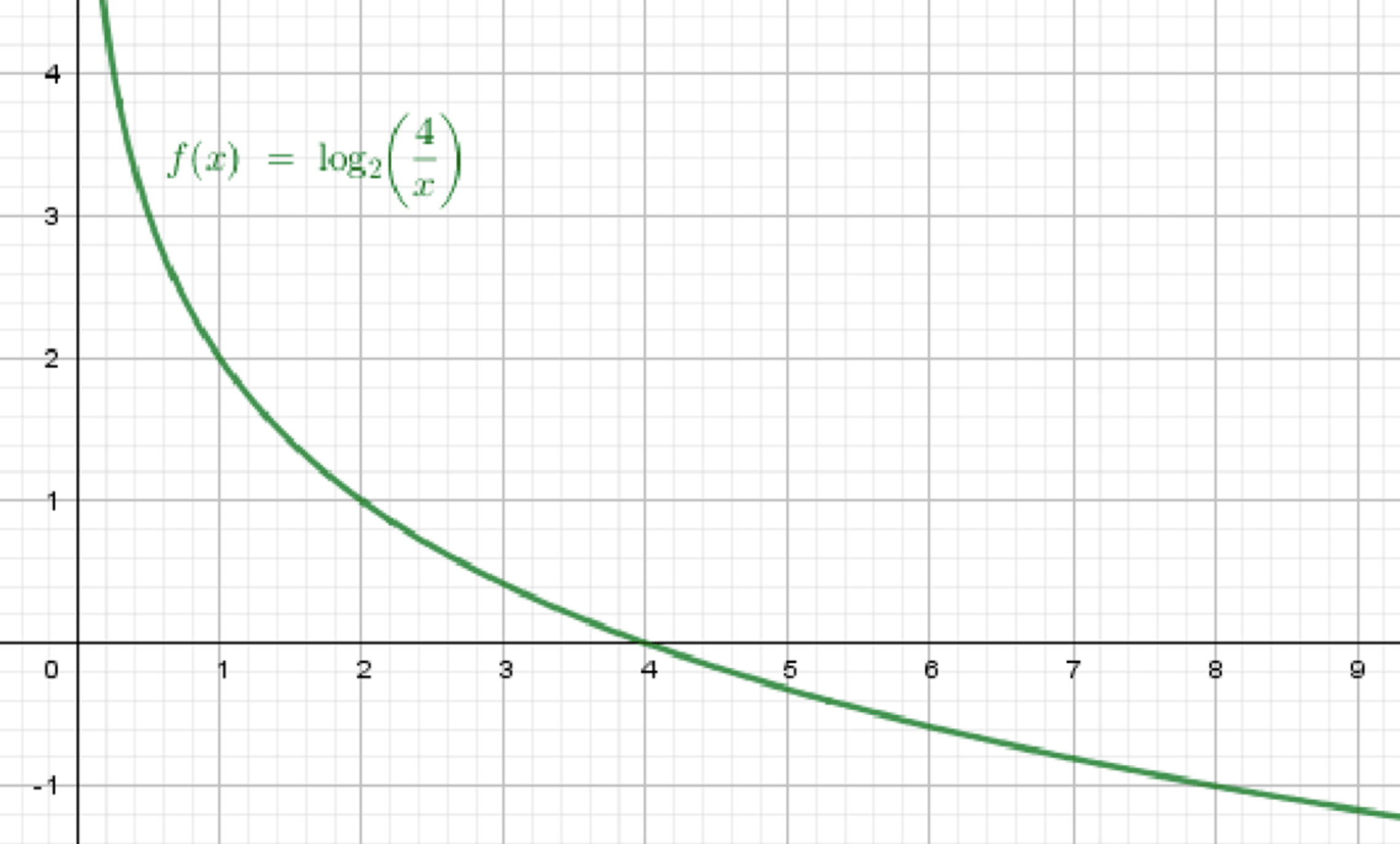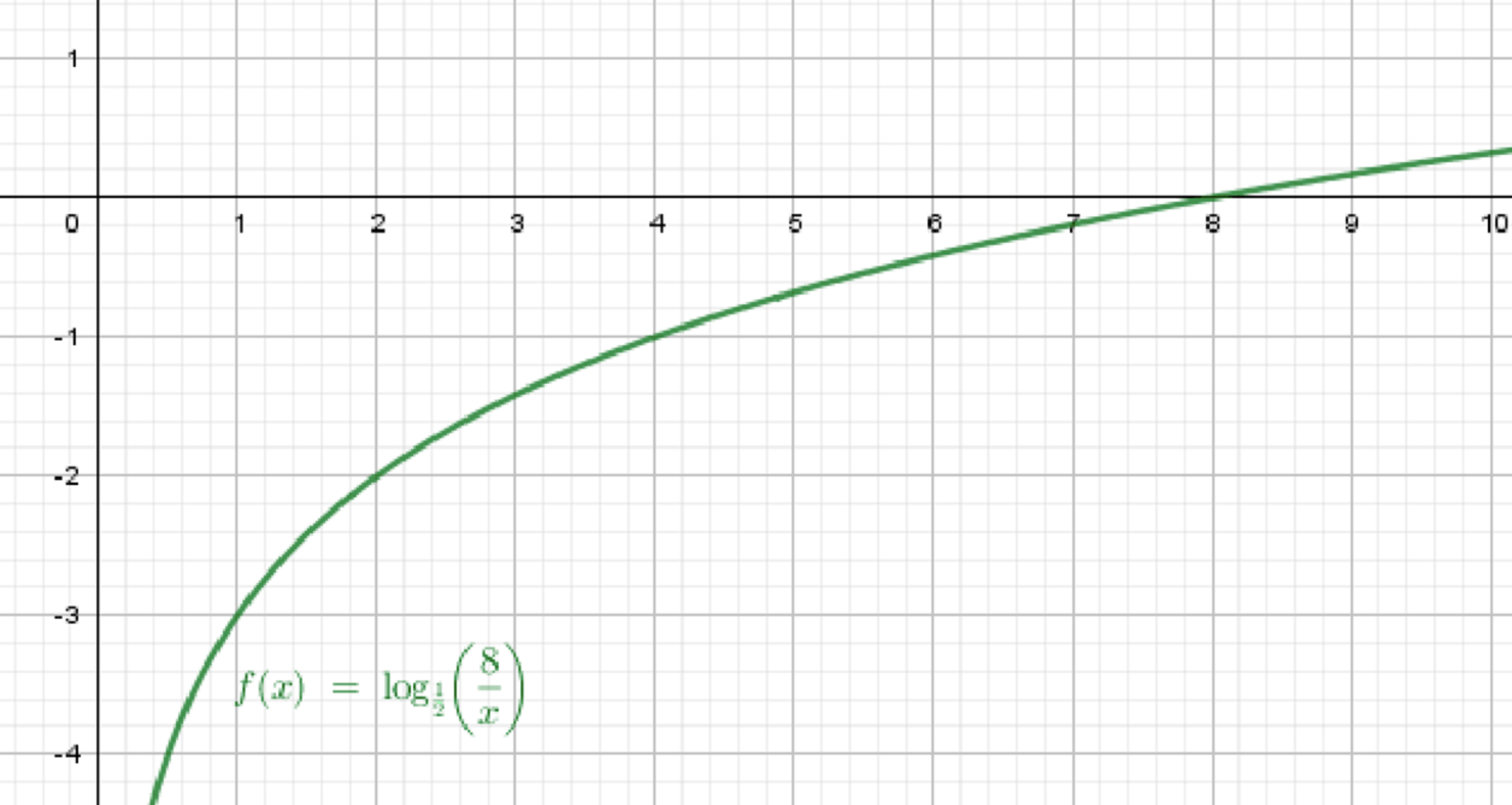ГДЗ 10-11 Класс Номер 43.39 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y={\log }_2\frac{4}{x}$

б) $y={\log }_{\frac{1}{3}}\frac{x^3}{27}$

в) $y={\log }_{3}9x^3$

г) $y={\log }_{\frac{1}{2}}\frac{8}{x}$

Построить график функции:

а) $y = \log_2 \frac{4}{x} = \log_2 4 — \log_2 x = 2 — \log_2 x$;
Построим график функции $y = \log_2 x$;
Отразим его относительно оси абсцисс;
Переместим его на 2 единицы вверх:

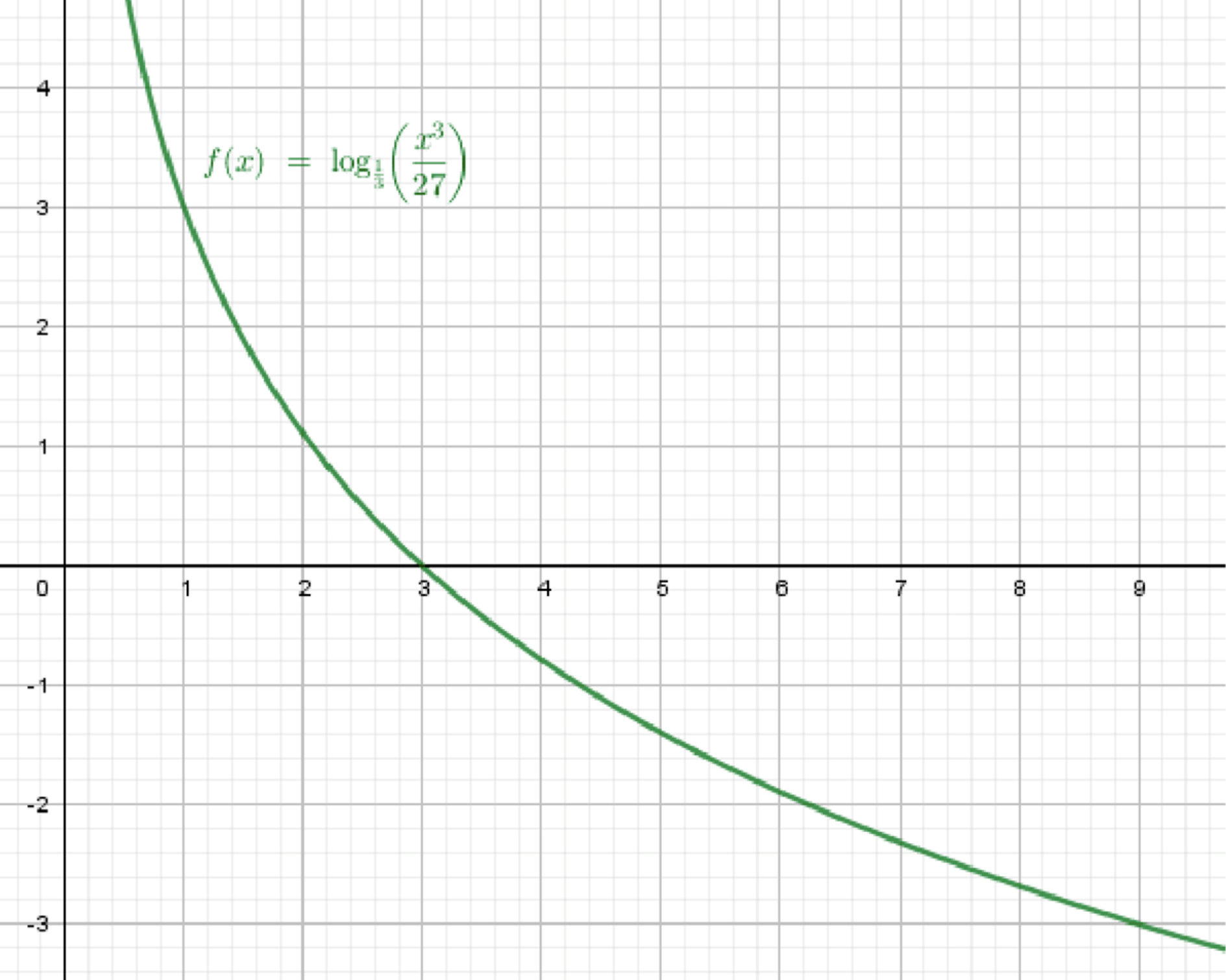
б) $y = \log_{\frac{1}{3}} \frac{x^3}{27} = \log_{\frac{1}{3}} x^3 + \log_{\frac{1}{3}} \frac{1}{27} = 3 \log_{\frac{1}{3}} x + 3$;
Построим график функции $y = \log_{\frac{1}{3}} x$;
Растянем его в 3 раза от оси абсцисс;
Переместим его на 3 единицы вверх:

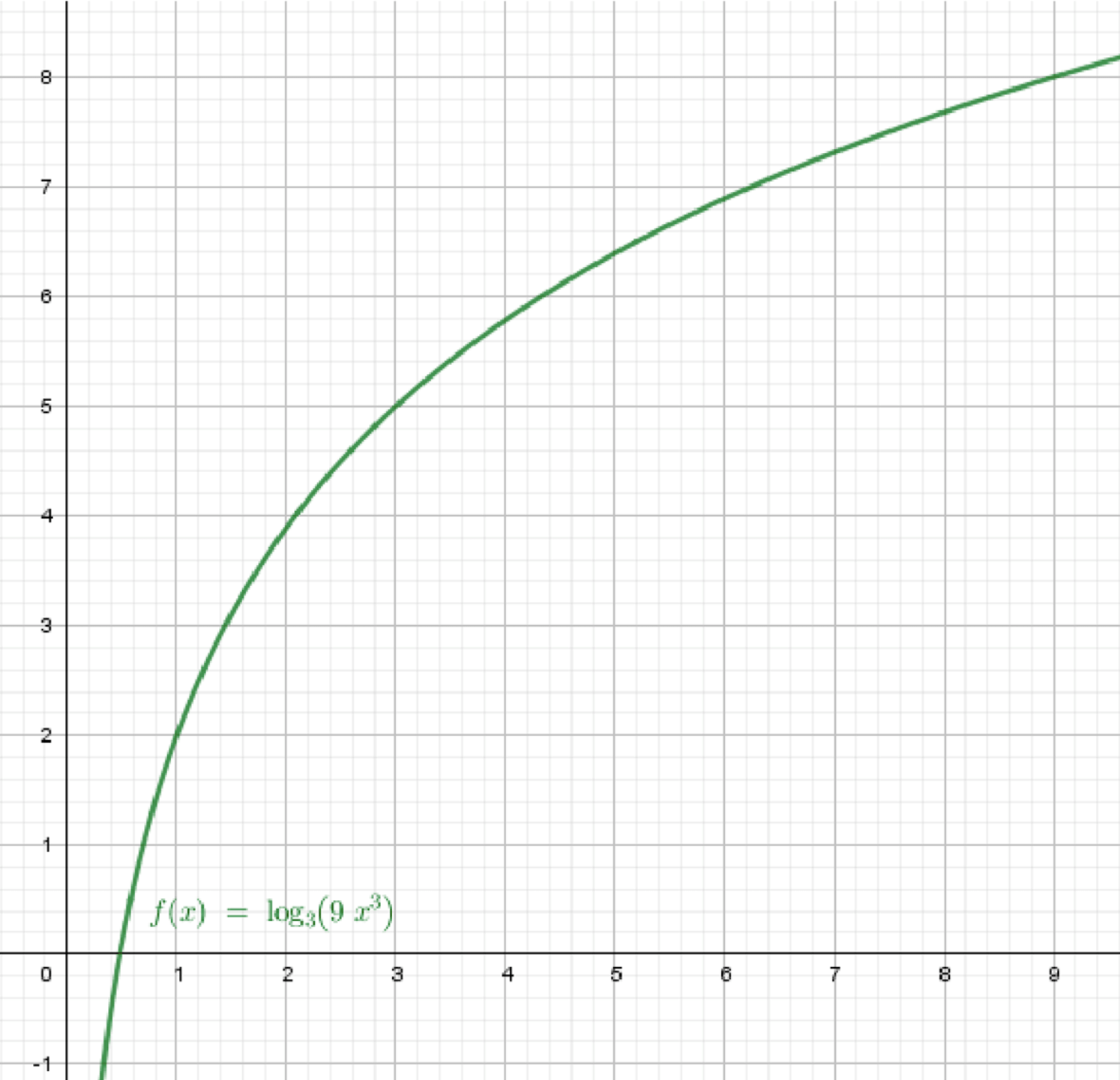
в) $y = \log_3 9x^3 = \log_3 9 + \log_3 x^3 = 2 + 3 \log_3 x$;
Построим график функции $y = \log_3 x$;
Растянем его в 3 раза от оси абсцисс;
Переместим его на 2 единицы вверх:

г) $y = \log_{\frac{1}{2}} \frac{8}{x} = \log_{\frac{1}{2}} 8 — \log_{\frac{1}{2}} x = -3 — \log_{\frac{1}{2}} x$;
Построим график функции $y = \log_{\frac{1}{2}} x$;
Отразим его относительно оси абсцисс;
Переместим его на 3 единицы вниз:

а)

Функция:

$$y = \log_2 \left( \frac{4}{x} \right)$$

Шаг 1. Разложим логарифм дроби по формуле:

$$\log_2 \left( \frac{4}{x} \right) = \log_2 4 — \log_2 x$$

Шаг 2. Вычислим $\log_2 4 = \log_2 (2^2) = 2$

Шаг 3. Получаем:

$$y = 2 — \log_2 x$$

Шаг 4. Преобразуем:

$$y = -\log_2 x + 2$$

Анализ:

• График $y = \log_2 x$: возрастает, проходит через $(1, 0)$, область определения: $x > 0$
• Минус перед логарифмом: отражение относительно оси абсцисс
• Прибавление 2: сдвиг графика вверх на 2 единицы

Итог:
График функции $y = \log_2 \left( \frac{4}{x} \right)$ получается из графика $y = \log_2 x$:

• сначала отражением относительно оси $x$,
• затем сдвигом вверх на 2 единицы

б)

Функция:

$$y = \log_{\frac{1}{3}} \left( \frac{x^3}{27} \right)$$

Шаг 1. Разложим на сумму логарифмов:

$$\log_{\frac{1}{3}} x^3 — \log_{\frac{1}{3}} 27$$

Шаг 2. Применим формулу:

$$\log_{\frac{1}{3}} x^3 = 3 \log_{\frac{1}{3}} x$$ $$\log_{\frac{1}{3}} 27 = \log_{\frac{1}{3}} (3^3) = 3 \cdot \log_{\frac{1}{3}} 3 = 3 \cdot (-1) = -3$$

Шаг 3. Получаем:

$$y = 3 \log_{\frac{1}{3}} x + 3$$

Анализ:

• Базовая функция $y = \log_{\frac{1}{3}} x$: убывающая, определена при $x > 0$
• Умножение на 3: растяжение графика от оси $x$ в 3 раза
• Прибавление 3: сдвиг графика вверх на 3 единицы

Итог:
График функции $y = \log_{\frac{1}{3}} \left( \frac{x^3}{27} \right)$ строится из $y = \log_{\frac{1}{3}} x$:

• сначала растяжением вверх в 3 раза,
• затем сдвигом вверх на 3 единицы

в)

Функция:

$$y = \log_3 (9x^3)$$

Шаг 1. Разложим по свойствам логарифма:

$$\log_3 9 + \log_3 x^3$$

Шаг 2. Вычислим:

$$\log_3 9 = \log_3 (3^2) = 2, \quad \log_3 x^3 = 3 \log_3 x$$

Шаг 3. Получаем:

$$y = 2 + 3 \log_3 x$$

Анализ:

• $y = \log_3 x$ — возрастает, определена при $x > 0$
• Умножение на 3: растяжение вверх от оси абсцисс в 3 раза
• Прибавление 2: сдвиг вверх на 2 единицы

Итог:
График функции $y = \log_3 (9x^3)$ получается из $y = \log_3 x$:

• сначала растяжением от оси $x$ в 3 раза,
• затем сдвигом вверх на 2 единицы

г)

Функция:

$$y = \log_{\frac{1}{2}} \left( \frac{8}{x} \right)$$

Шаг 1. Разложим логарифм:

$$\log_{\frac{1}{2}} 8 — \log_{\frac{1}{2}} x$$

Шаг 2. Вычислим:

$$\log_{\frac{1}{2}} 8 = \log_{\frac{1}{2}} (2^3) = 3 \cdot \log_{\frac{1}{2}} 2 = 3 \cdot (-1) = -3$$

Шаг 3. Получаем:

$$y = -3 — \log_{\frac{1}{2}} x = -\log_{\frac{1}{2}} x — 3$$

Анализ:

• Базовая функция $y = \log_{\frac{1}{2}} x$ — убывающая
• Умножение на $-1$: отражение относительно оси абсцисс
• $-3$: сдвиг вниз на 3 единицы

Итог:
График $y = \log_{\frac{1}{2}} \left( \frac{8}{x} \right)$ строится из $y = \log_{\frac{1}{2}} x$:

• сначала отражением относительно оси $x$,
• затем сдвигом вниз на 3 единицы