ГДЗ 10-11 Класс Номер 47.1 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = e^{x+4}$;

б) $y = e^{-x} + 1$;

в) $y = e^{x-3}$;

г) $y = e^{x-2} — 3$

Построить график функции:

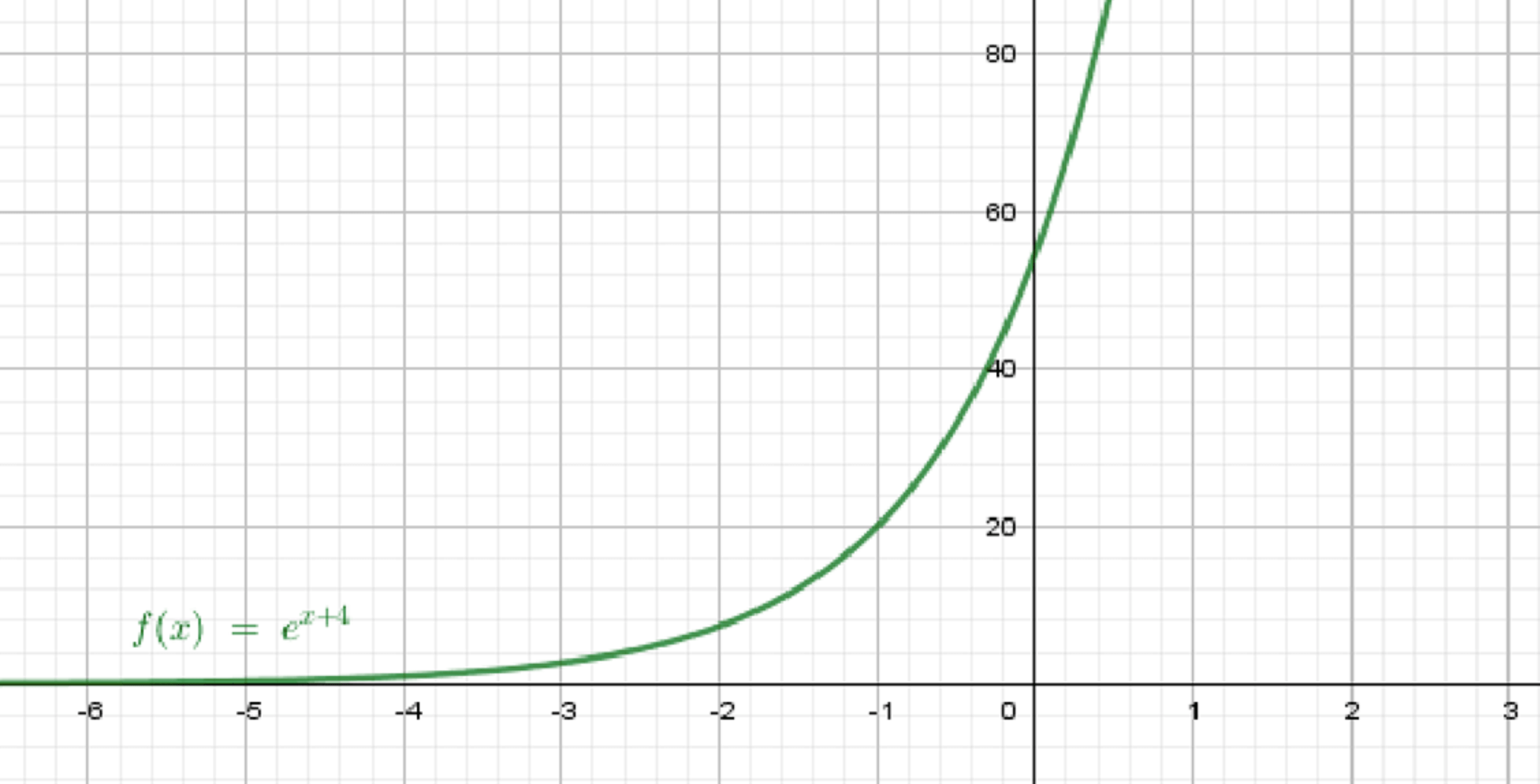
а) $y = e^{x+4}$;

Построим график функции $y = e^x$;

Переместим его на 4 единицы влево:

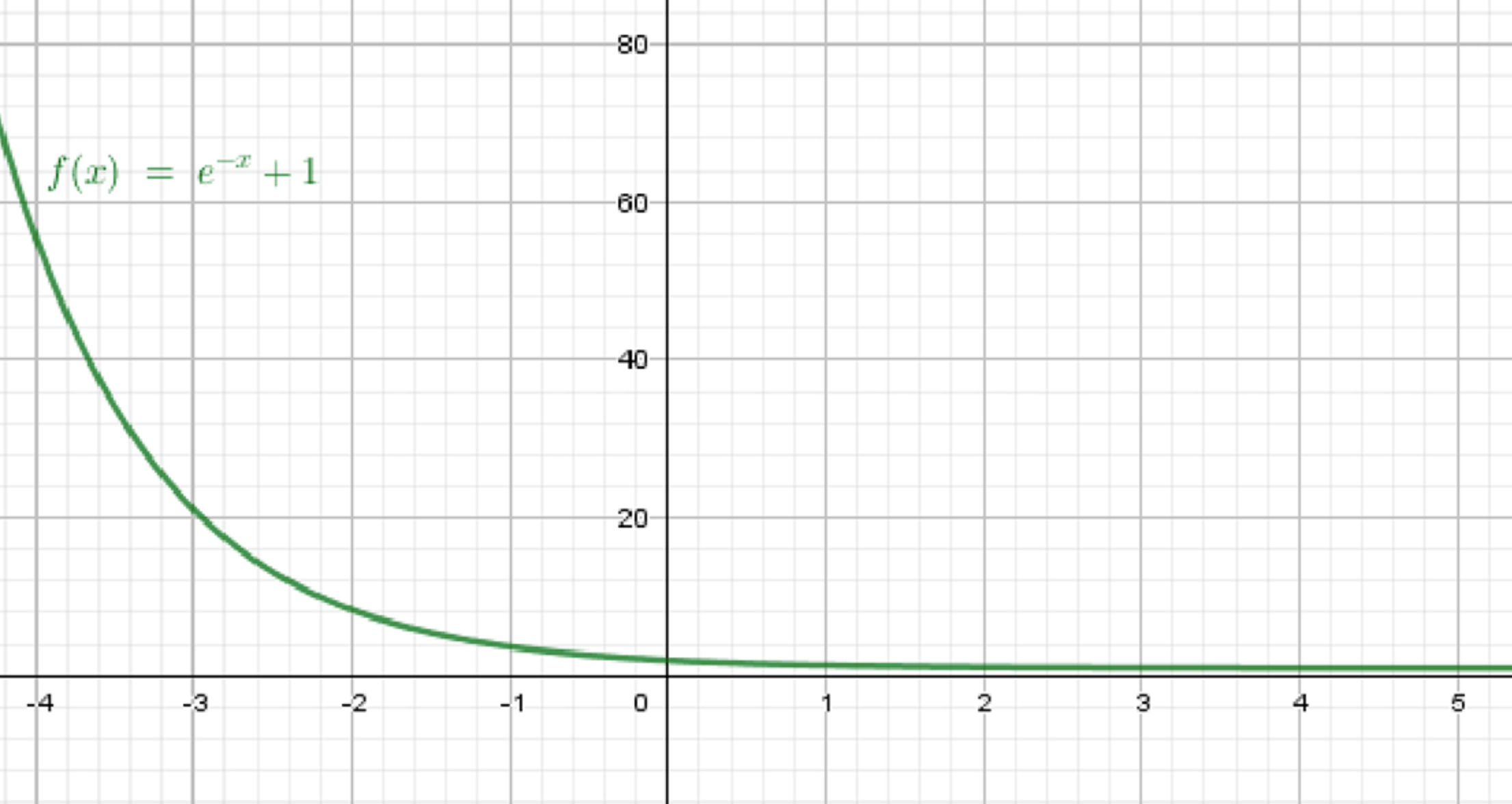
б) $y = e^{-x} + 1$;

Построим график функции $y = e^x$;

Отразим его относительно оси ординат;

Переместим его на 1 единицу вверх:

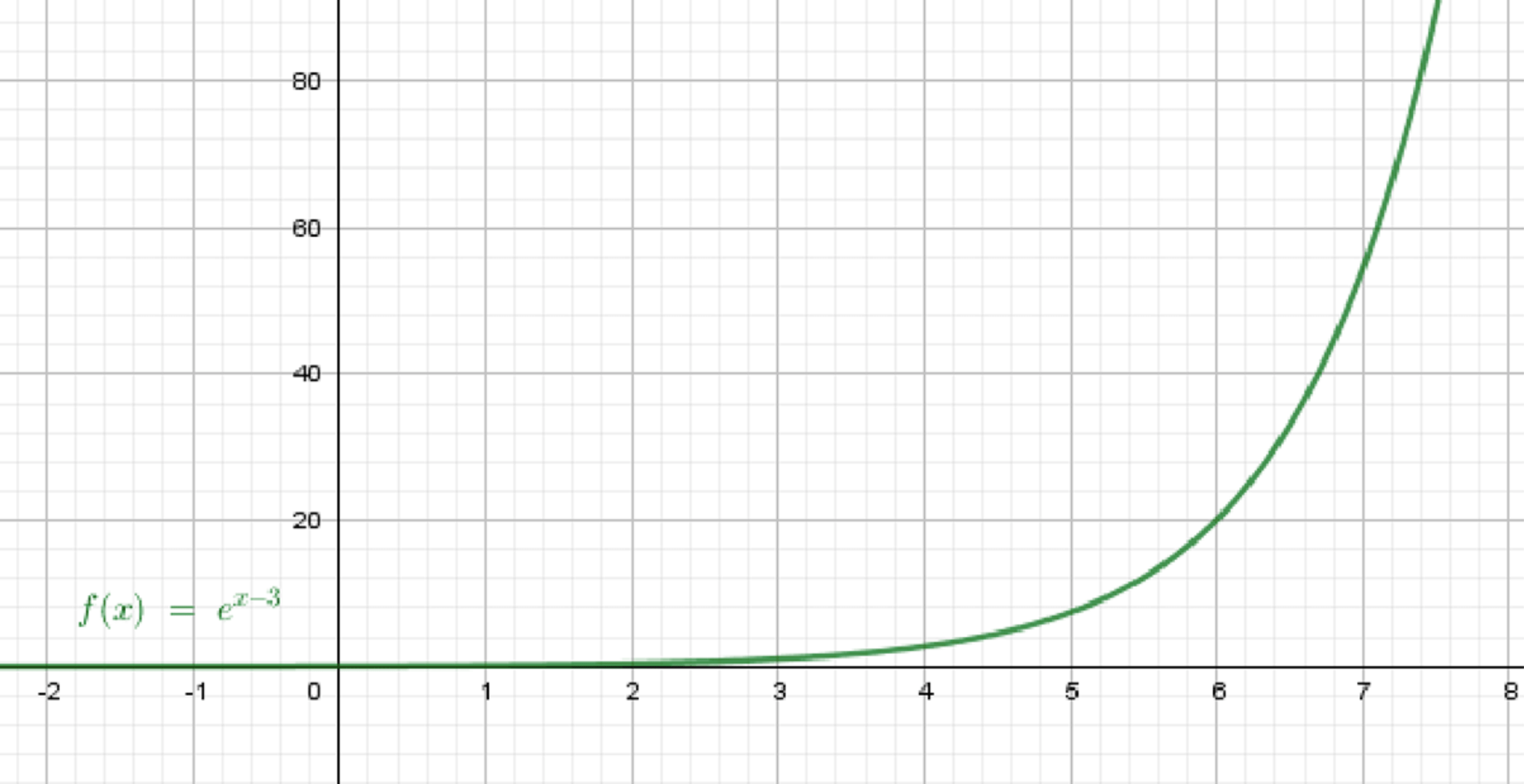
в) $y = e^{x-3}$;

Построим график функции $y = e^x$;

Переместим его на 3 единицы вправо:

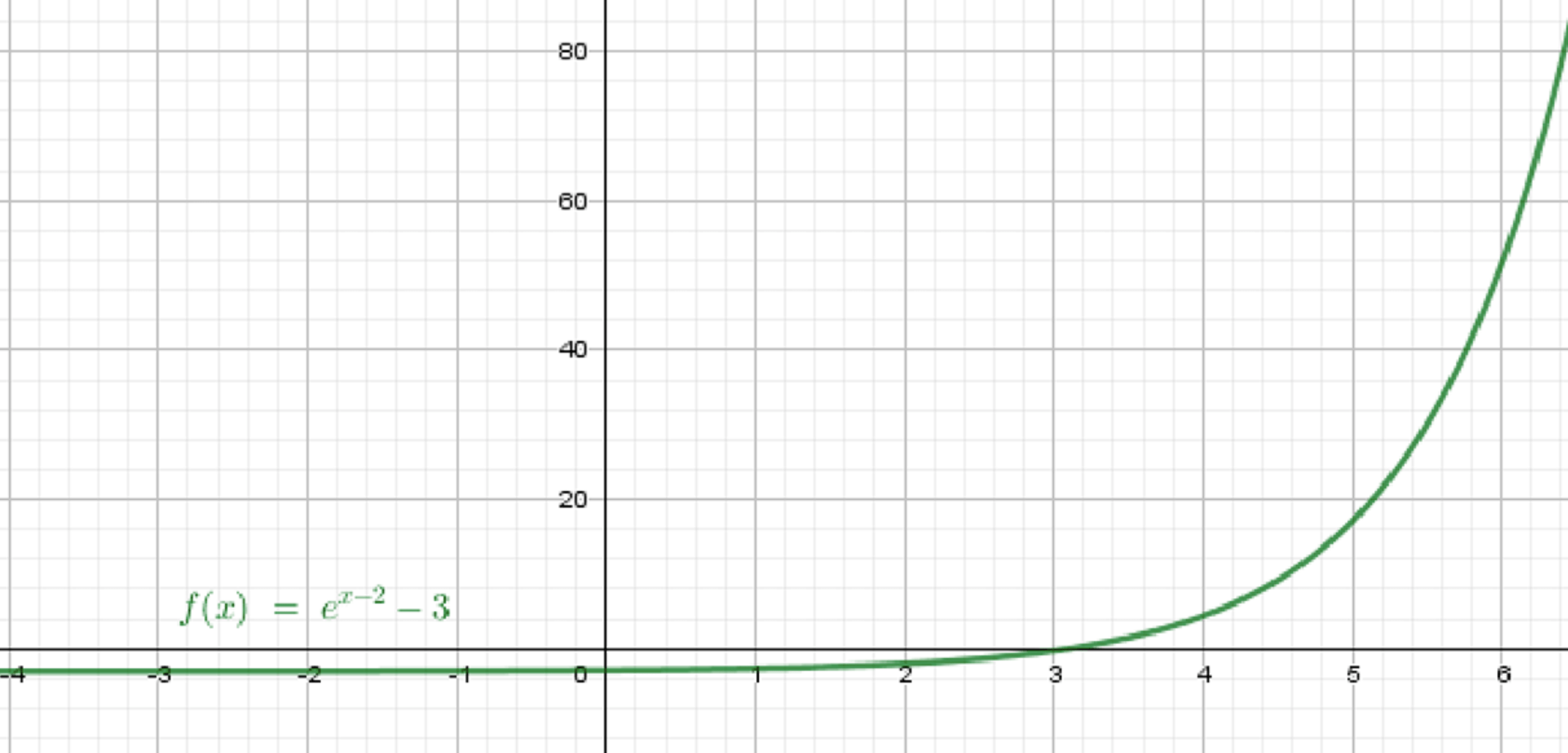
г) $y = e^{x-2} — 3$;

Построим график функции $y = e^x$;

Переместим его на 2 единицы вправо;

Переместим его на 3 единицы вниз:

а) $y = e^{x + 4}$

Шаг 1. Базовая функция

Рассматриваем базовую экспоненциальную функцию:

$$y = e^x$$

Свойства графика $y = e^x$:

• Область определения: $(-\infty;\ +\infty)$
• Область значений: $(0;\ +\infty)$
• График проходит через точку $(0; 1)$
• График возрастает
• Асимптота: прямая $y = 0$ (ось абсцисс)

Шаг 2. Сдвиг влево на 4 единицы

Функция $y = e^{x + 4}$ получается из $y = e^x$ сдвигом графика на 4 единицы влево по оси $x$.

Что происходит с графиком:

• Каждая точка графика $y = e^x$ смещается на 4 единицы влево
• Точка $(0; 1)$ переходит в $(-4; 1)$
• График остаётся возрастающим
• Асимптота остаётся прежней: $y = 0$

Вывод: график — это возрастающая кривая, прижатая к оси $x$ слева и стремящаяся вверх справа, но начальная точка $(0; 1)$ сместилась влево к $(-4; 1)$

б) $y = e^{-x} + 1$

Шаг 1. Базовая функция

Начинаем с $y = e^x$ — стандартной экспоненты.

Шаг 2. Отражение

Переходим к $y = e^{-x}$. Это отражение графика $y = e^x$ относительно оси $y$ (орднат).

Что происходит:

• График становится убывающим
• Точка $(0; 1)$ остаётся на месте
• Область определения: $(-\infty; +\infty)$
• Область значений: $(0;\ +\infty)$
• Асимптота: $y = 0$

Шаг 3. Сдвиг вверх на 1 единицу

Теперь прибавляем 1: $y = e^{-x} + 1$

Что происходит:

• Весь график поднимается на 1 вверх
• Точка $(0; 1)$ становится $(0; 2)$
• Асимптота сдвигается: теперь это $y = 1$

Вывод: убывающая экспоненциальная кривая, стремится к $y = 1$ слева, убывает и проходит через $(0; 2)$, идёт вниз, но никогда не пересекает асимптоту $y = 1$

в) $y = e^{x — 3}$

Шаг 1. Начинаем с графика $y = e^x$

Те же свойства, что выше.

Шаг 2. Сдвиг вправо на 3 единицы

Переход к $y = e^{x — 3}$ означает, что график сдвигается на 3 единицы вправо

Что происходит:

• Точка $(0; 1)$ становится $(3; 1)$
• График по-прежнему возрастает
• Асимптота остаётся: $y = 0$

Вывод: кривая, идущая из левого низа вверх, но «начинается» теперь в точке $(3; 1)$, где раньше была точка $(0; 1)$

г) $y = e^{x — 2} — 3$

Шаг 1. Исходная функция $y = e^x$

Начинаем с привычного графика экспоненты.

Шаг 2. Сдвиг вправо на 2 единицы

Переход к $y = e^{x — 2}$

• Сдвиг на 2 единицы вправо
• Точка $(0; 1)$ переходит в $(2; 1)$

Шаг 3. Сдвиг вниз на 3 единицы

Функция $y = e^{x — 2} — 3$

• График опускается на 3 единицы
• Точка $(2; 1)$ превращается в $(2; -2)$
• Асимптота теперь $y = -3$

Вывод: возрастающая экспоненциальная кривая, проходящая через точку $(2; -2)$, с горизонтальной асимптотой $y = -3$