ГДЗ 10-11 Класс Номер 49.30 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а)

$${\int }_0^{\sqrt{2}}\sqrt{4-x^2}dx;$$

б)

$${\int }_{-4}^4\sqrt{64-x^2}dx$$

Используя геометрические соображения, вычислить интеграл:

а)

$$\int_{0}^{\sqrt{2}} \sqrt{4 — x^2} \, dx;$$

Преобразуем данную функцию:

$$y = \sqrt{4 — x^2};$$ $$y^2 = 4 — x^2;$$ $$x^2 + y^2 = 4;$$

Дано уравнение окружности:

$$x_0 = 0, \quad y_0 = 0, \quad R = 2;$$

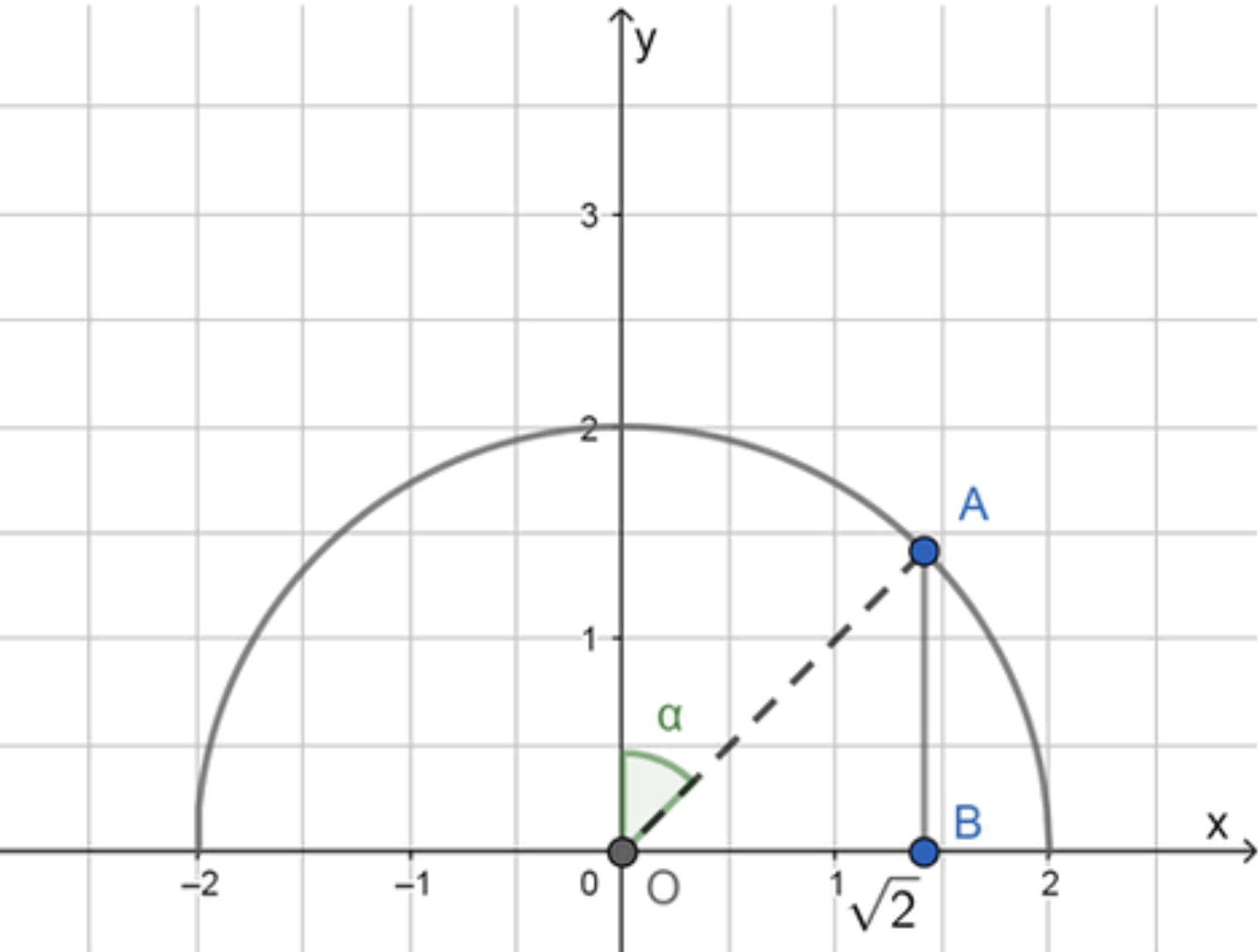
Отобразим условие задачи:

$OA = 2, \quad OB = \sqrt{2}, \quad \angle OAB = 90^\circ$;

$$AB = \sqrt{(OA)^2 — (OB)^2} = \sqrt{4 — 2} = \sqrt{2};$$ $$\angle AOB = 45^\circ \quad (OB = AB);$$ $$\angle \alpha = 90^\circ — 45^\circ = 45^\circ;$$

Площадь треугольника $OAB$:

$$S_1 = \frac{1}{2} \cdot AB \cdot OB = \frac{1}{2} \cdot \sqrt{2} \cdot \sqrt{2} = \frac{2}{2} = 1;$$

Площадь сектора с центральным углом $\alpha$:

$$S_2 = \frac{\pi R^2 \cdot \alpha}{360^\circ} = \frac{\pi \cdot 2^2 \cdot 45^\circ}{360^\circ} = \frac{180\pi}{360} = \frac{\pi}{2};$$

Значение интеграла:

$$\int_{0}^{\sqrt{2}} \sqrt{4 — x^2} \, dx = S_1 + S_2 = 1 + \frac{\pi}{2};$$

Ответ: $\frac{\pi}{2} + 1$.

б)

$$\int_{-4}^{4} \sqrt{64 — x^2} \, dx;$$

Преобразуем данную функцию:

$$y = \sqrt{64 — x^2};$$ $$y^2 = 64 — x^2;$$ $$x^2 + y^2 = 64;$$

Дано уравнение окружности:

$$x_0 = 0, \quad y_0 = 0, \quad R = 8;$$

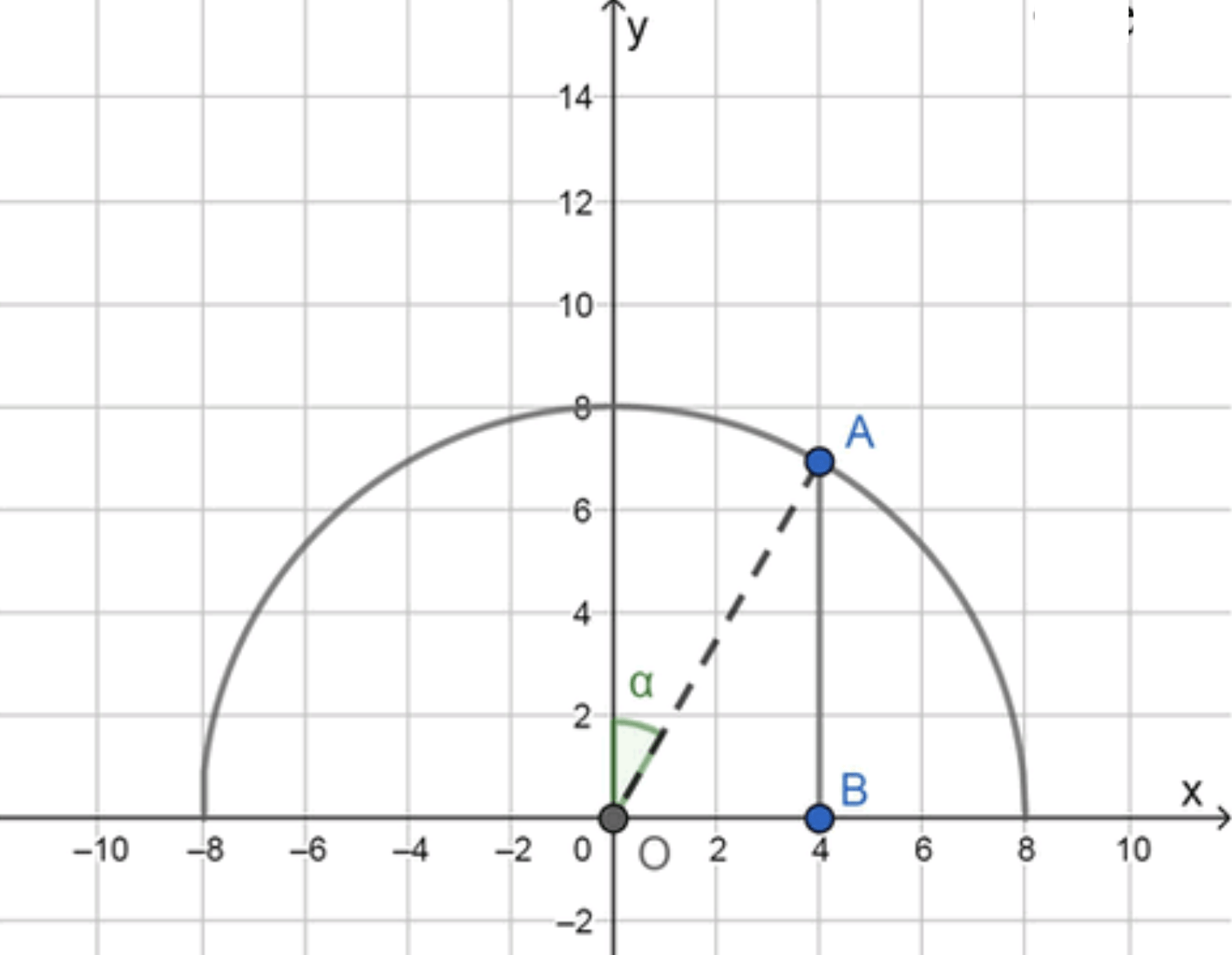
Отобразим условие задачи:

$OA = 8, \quad OB = 4, \quad \angle OAB = 90^\circ$;

$$AB = \sqrt{(OA)^2 — (OB)^2} = \sqrt{64 — 16} = \sqrt{48} = 4\sqrt{3};$$ $$\angle OAB = 30^\circ \quad (OB = \frac{1}{2} OA);$$ $$\angle \alpha = \angle OAB = 30^\circ;$$

Площадь треугольника $OAB$:

$$S_1 = \frac{1}{2} \cdot AB \cdot OB = \frac{1}{2} \cdot 4\sqrt{3} \cdot 4 = \frac{16\sqrt{3}}{2} = 8\sqrt{3};$$

Площадь сектора с центральным углом $\alpha$:

$$S_2 = \frac{\pi R^2 \cdot \alpha}{360^\circ} = \frac{\pi \cdot 8^2 \cdot 30^\circ}{360^\circ} = \frac{1920\pi}{360} = \frac{16\pi}{3};$$

Значение интеграла:

$$S = \int_{-4}^{4} \sqrt{64 — x^2} \, dx = 2(S_1 + S_2) = 2\left(\frac{16\pi}{3} + 8\sqrt{3}\right);$$ $$S = \frac{16}{3}(2\pi + 3\sqrt{3}) = \frac{16\pi}{3} \cdot 2 + 16\sqrt{3} = \frac{16}{3}(2\pi + 3\sqrt{3});$$

Ответ: $\frac{16}{3}(2\pi + 3\sqrt{3})$.

а)

$$\int_{0}^{\sqrt{2}} \sqrt{4 — x^2} \, dx$$

Шаг 1. Анализ подынтегральной функции

Подынтегральная функция:

$$y = \sqrt{4 — x^2}$$

Возведем обе части в квадрат:

$$y^2 = 4 — x^2 \Rightarrow x^2 + y^2 = 4$$

Это — уравнение окружности радиуса $R = 2$ с центром в начале координат $(0, 0)$.

Шаг 2. Геометрическая интерпретация

Так как $y = \sqrt{4 — x^2}$, то берётся только верхняя полуокружность (неотрицательные значения $y$).

Интеграл $\int_0^{\sqrt{2}} \sqrt{4 — x^2} dx$ вычисляет площадь под графиком этой функции от $x = 0$ до $x = \sqrt{2}$, то есть часть верхней полуокружности от точки на оси $x = 0$ до точки на оси $x = \sqrt{2}$.

Шаг 3. Построение геометрической фигуры

Рассмотрим треугольник $OAB$, где:

• $O = (0, 0)$ — центр окружности,
• $B = (\sqrt{2}, 0)$ — правая граница интегрирования на оси $x$,
• $A = (0, \sqrt{2})$ — соответствующая точка на окружности, т.к. $x^2 + y^2 = 4 \Rightarrow y = \sqrt{4 — x^2} = \sqrt{2}$ при $x = 0$.

Таким образом:

• $OA = 2$ (радиус),
• $OB = \sqrt{2}$,
• $AB = \sqrt{OA^2 — OB^2} = \sqrt{4 — 2} = \sqrt{2}$ по теореме Пифагора (треугольник прямоугольный),
• Угол $AOB = 45^\circ$, так как $OB = AB$ — треугольник равнобедренный, а $\angle OAB = 90^\circ$.

Шаг 4. Площадь фигуры под графиком

Площадь под графиком состоит из:

1. Площади сектора с центральным углом $\alpha = 45^\circ$
2. Площади треугольника $OAB$

1. Площадь сектора:

$$S_{\text{сектора}} = \frac{\alpha}{360^\circ} \cdot \pi R^2 = \frac{45^\circ}{360^\circ} \cdot \pi \cdot 2^2 = \frac{1}{8} \cdot 4\pi = \frac{\pi}{2}$$

2. Площадь треугольника:

$$S_{\text{треугольника}} = \frac{1}{2} \cdot AB \cdot OB = \frac{1}{2} \cdot \sqrt{2} \cdot \sqrt{2} = \frac{2}{2} = 1$$

Шаг 5. Сумма площадей

$$\int_{0}^{\sqrt{2}} \sqrt{4 — x^2} dx = S_{\text{треугольника}} + S_{\text{сектора}} = 1 + \frac{\pi}{2}$$

Ответ:

$$\frac{\pi}{2} + 1$$

б)

$$\int_{-4}^{4} \sqrt{64 — x^2} \, dx$$

Шаг 1. Анализ подынтегральной функции

Рассматриваем:

$$y = \sqrt{64 — x^2} \Rightarrow y^2 = 64 — x^2 \Rightarrow x^2 + y^2 = 64$$

Это уравнение окружности радиуса $R = 8$, с центром в начале координат $(0, 0)$. Функция $y = \sqrt{64 — x^2}$ описывает верхнюю полуокружность.

Шаг 2. Геометрический смысл интеграла

Интеграл:

$$\int_{-4}^{4} \sqrt{64 — x^2} dx$$

— это площадь под верхней полуокружностью от $x = -4$ до $x = 4$, то есть симметричная часть, половина окружности, но только между $x = -4$ и $x = 4$, а не вся полуокружность.

Шаг 3. Построение фигуры

Рассмотрим фигуру, ограниченную:

• дугой окружности радиуса 8,
• вертикальными прямыми $x = -4$ и $x = 4$,
• осью $x$ (нижняя граница).

Из геометрии:

• $OA = 8$,
• $OB = 4$,
• Треугольник $OAB$ прямоугольный (по построению),
• По теореме Пифагора:

$$AB = \sqrt{OA^2 — OB^2} = \sqrt{64 — 16} = \sqrt{48} = 4\sqrt{3}$$

Рассмотрим угол:

$$OB = \frac{1}{2} OA \Rightarrow \angle OAB = 30^\circ \Rightarrow \angle \alpha = 30^\circ$$

Шаг 4. Площадь одной половины (справа от оси)

Сначала вычислим площадь справа (от $x = 0$ до $x = 4$), затем удвоим.

1. Площадь треугольника:

$$S_1 = \frac{1}{2} \cdot AB \cdot OB = \frac{1}{2} \cdot 4\sqrt{3} \cdot 4 = \frac{16\sqrt{3}}{2} = 8\sqrt{3}$$

2. Площадь сектора с центральным углом $30^\circ$:

$$S_2 = \frac{30^\circ}{360^\circ} \cdot \pi R^2 = \frac{1}{12} \cdot \pi \cdot 64 = \frac{64\pi}{12} = \frac{16\pi}{3}$$

Шаг 5. Удвоим (слева и справа)

Общая площадь под графиком:

$$S = 2(S_1 + S_2) = 2\left(8\sqrt{3} + \frac{16\pi}{3}\right)$$

Шаг 6. Преобразование выражения

Вынесем общий множитель $\frac{16}{3}$:

$$S = \frac{16}{3}(3\sqrt{3} + 2\pi)$$

Ответ:

$$\frac{16}{3}(2\pi + 3\sqrt{3})$$