ГДЗ 10-11 Класс Номер 49.33 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

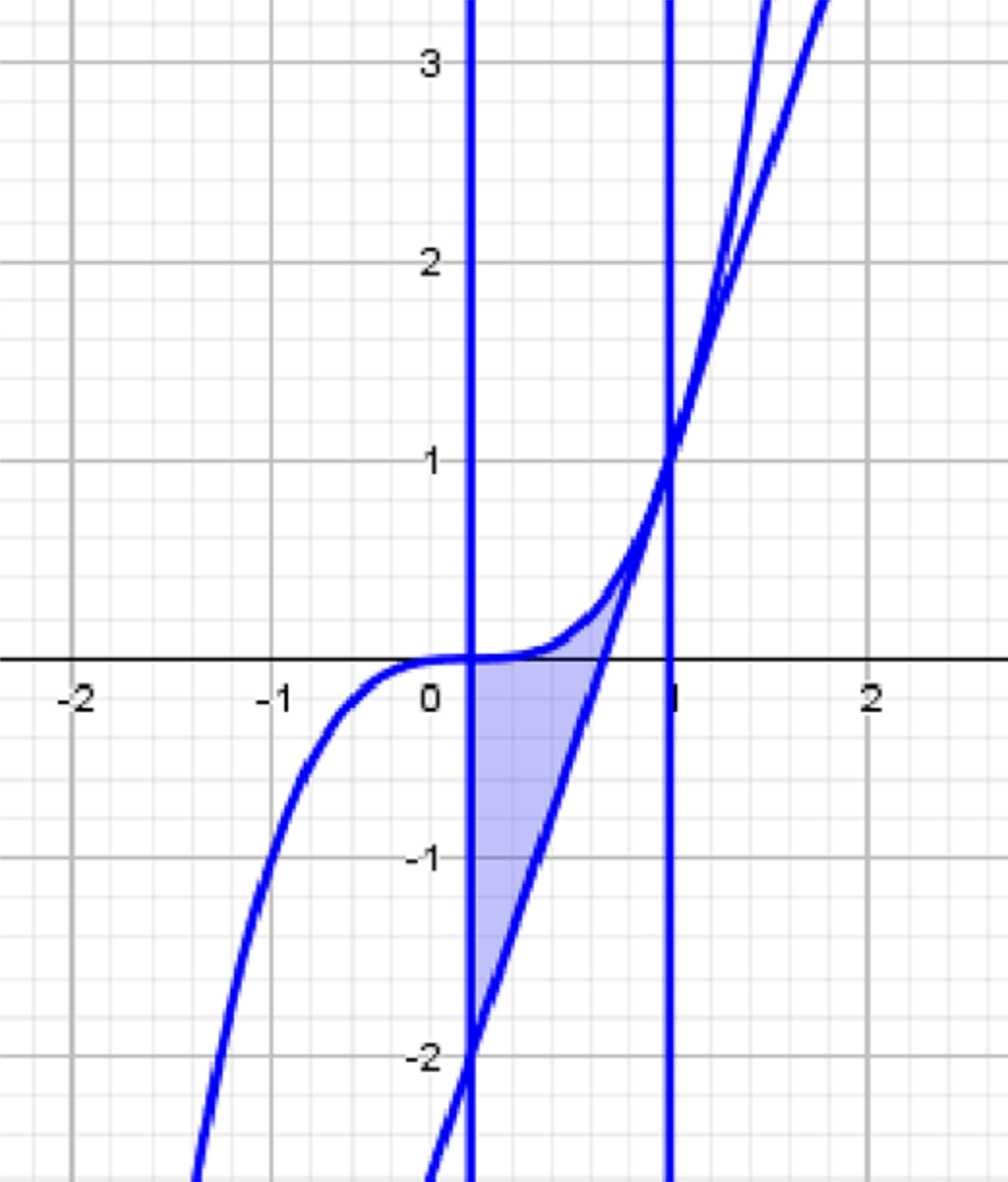
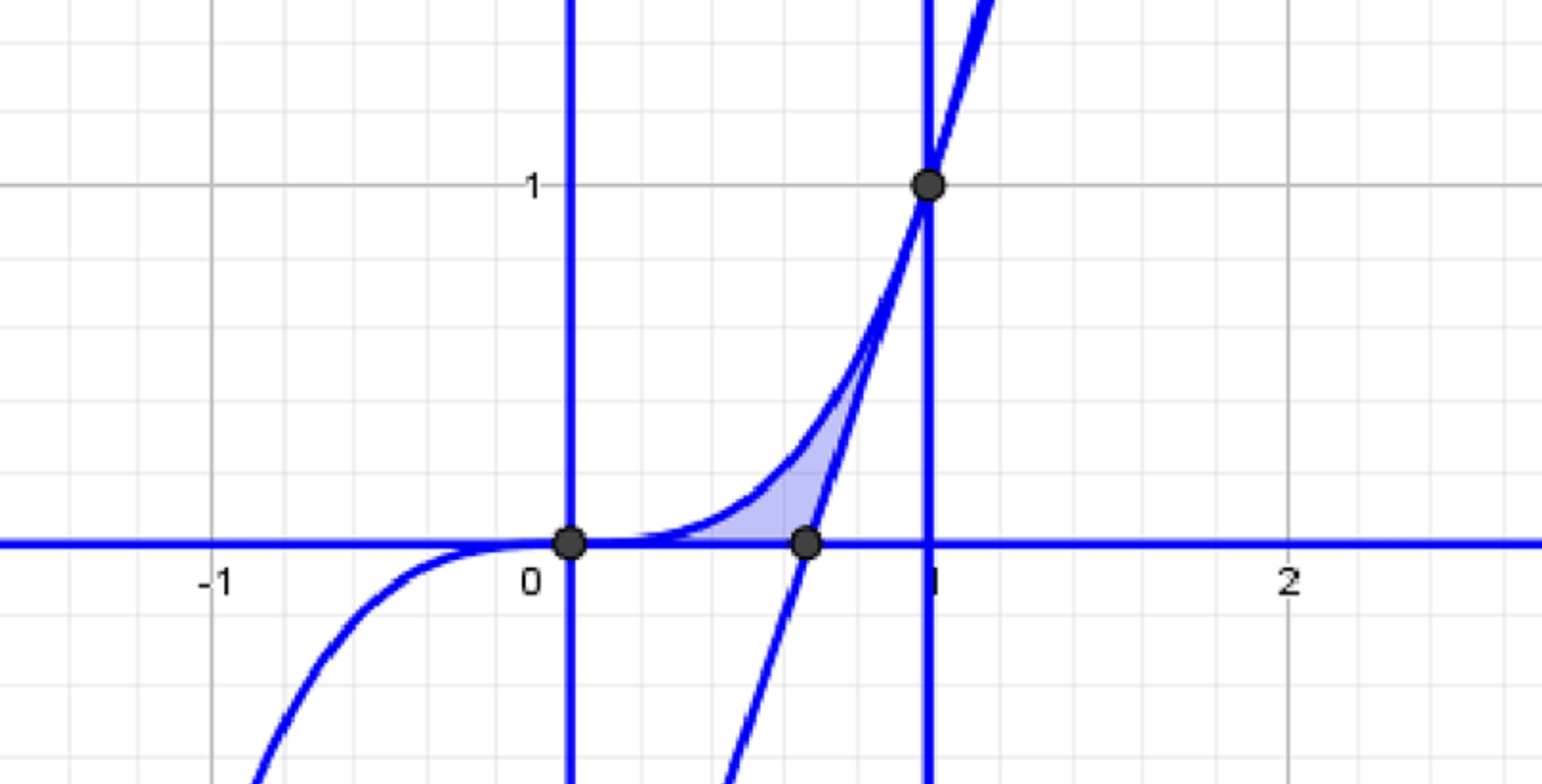
а) Найдите площадь фигуры, ограниченной графиком функции у = x³, касательной к нему в точке x = 1 и осью у.

б) Найдите площадь фигуры, ограниченной графиком функции у = x³ и касательными к нему в точках x = 0 и x = 1.

Найти площадь фигуры, ограниченной графиком функции:

а) $f(x)=x^3$, касательной в точке $x_0=1$ и осью $y$;
Уравнение касательной:

$$f^{\mathrm{\prime }}(x)=(x^3{)}^{\mathrm{\prime }}=3x^2;$$$$f^{\mathrm{\prime }}(1)=3\cdot 1^2=3;$$$$f(1)=1^3=1;$$$$y=f^{\mathrm{\prime }}(x_0)(x-x_0)+f(x_0);$$$$y=3(x-1)+1=3x-3+1=3x-2;$$

Графики функций:

Площадь искомой фигуры:

$$S={\int }_0^1(x^3-(3x-2))dx=(\frac{x^4}{4}-(\frac{3x^2}{2}-2x)){\mid }_0^1;$$$$S=(\frac{x^4}{4}-\frac{3x^2}{2}+2x){\mid }_0^1;$$$$S=(\frac{1^4}{4}-\frac{3\cdot 1^2}{2}+2\cdot 1)-(\frac{0^4}{4}-\frac{3\cdot 0^2}{2}+2\cdot 0)=\frac{1}{4}-\frac{3}{2}+2-0;$$$$S=\frac{1-3\cdot 2+2\cdot 4}{4}=\frac{3}{4};$$

Ответ: $\frac{3}{4}$

б) $f(x)=x^3$ и касательными в точках $x_{01}=0$ и $x_{02}=1$;
Уравнения касательных:

$$f^{\mathrm{\prime }}(x)=(x^3{)}^{\mathrm{\prime }}=3x^2;$$$$f^{\mathrm{\prime }}(0)=3\cdot 0^2=0,f^{\mathrm{\prime }}(1)=3\cdot 1^2=3;$$$$f(0)=0^3=0,f(1)=1^3=1;$$$$y=f^{\mathrm{\prime }}(x_0)(x-x_0)+f(x_0);$$$$y_1=0\cdot (x-0)+0=0;$$$$y_2=3(x-1)+1=3x-3+1=3x-2;$$

Графики функций:

Нули касательной:

$$3x-2=0;$$$$3x=2;$$$$x=\frac{2}{3};$$

Площадь искомой фигуры:

$$S={\int }_0^1{x}^{3}dx-{\int }_{2\mathrm{/}3}^1(3x-2)dx={\frac{x^4}{4}\mid }_0^1-{(\frac{3x^2}{2}-2x)\mid }_{2\mathrm{/}3}^1;$$$$S=(\frac{1^4}{4}-0)-(\frac{3\cdot 1^2}{2}-2\cdot 1)+(\frac{3}{2}\cdot {\left(\frac{2}{3}\right)}^2-2\cdot \frac{2}{3});$$$$S=\frac{1}{4}-(\frac{3}{2}-2)+(\frac{3}{2}\cdot \frac{4}{9}-\frac{4}{3});$$$$S=\frac{1}{4}-(-\frac{1}{2})+(\frac{2}{3}-\frac{4}{3});$$$$S=\frac{1}{4}+\frac{1}{2}-\frac{2}{3}=\frac{3-3\cdot 6+2\cdot 12-2\cdot 4}{12}=\frac{1}{12};$$

Ответ: $\frac{1}{12}$

а) $f(x)=x^3$, касательной в точке $x_0=1$, и осью $Oy$ (осью $y$)

Шаг 1. Найдём значение функции в точке касания

$$f(1)=1^3=1$$

Шаг 2. Найдём производную функции

$$f^{\mathrm{\prime }}(x)=\frac{d}{dx}(x^3)=3x^2$$

Шаг 3. Найдём угловой коэффициент касательной

$$f^{\mathrm{\prime }}(1)=3\cdot 1^2=3$$

Шаг 4. Уравнение касательной к графику функции в точке $x=1$

Общий вид касательной в точке $x_0$:

$$y=f^{\mathrm{\prime }}(x_0)(x-x_0)+f(x_0)$$

Подставим:

$$y=3(x-1)+1=3x-3+1=3x-2$$

Шаг 5. Границы интегрирования

Ось $Oy$ соответствует значению $x=0$.
Итак, фигура ограничена:

• Слева: $x=0$,
• Справа: $x=1$,
• Сверху: графиком функции $f(x)=x^3$,
• Снизу: касательной $y=3x-2$

Шаг 6. Составим выражение для площади

$$S={\int }_0^1(x^3-(3x-2))dx={\int }_0^1(x^3-3x+2)dx$$

Шаг 7. Найдём первообразную

$$\int (x^3-3x+2)dx=\frac{x^4}{4}-\frac{3x^2}{2}+2x$$

Шаг 8. Вычислим определённый интеграл

$$S=(\frac{x^4}{4}-\frac{3x^2}{2}+2x){\mid }_0^1$$

В верхнем пределе ($x=1$):

$$\frac{1^4}{4}-\frac{3\cdot 1^2}{2}+2\cdot 1=\frac{1}{4}-\frac{3}{2}+2$$

В нижнем пределе ($x=0$):

$$0-0+0=0$$

Шаг 9. Вычислим разность значений

$$S=(\frac{1}{4}-\frac{3}{2}+2)-0=\frac{1}{4}-\frac{3}{2}+2$$

Приведём к общему знаменателю:

$$=\frac{1}{4}-\frac{6}{4}+\frac{8}{4}=\frac{3}{4}$$

Шаг 10. Ответ

Ответ: $\boxed{{\displaystyle \frac{3}{4}}}$

б) $f(x)=x^3$, касательные в точках $x_1=0$ и $x_2=1$

Шаг 1. Найдём значение функции и производной в точках касания

Для $x=0$:

$$f(0)=0^3=0,f^{\mathrm{\prime }}(0)=3\cdot 0^2=0$$

Для $x=1$:

$$f(1)=1^3=1,f^{\mathrm{\prime }}(1)=3\cdot 1^2=3$$

Шаг 2. Найдём уравнения касательных

Касательная в точке $x=0$:

$$y=f^{\mathrm{\prime }}(0)(x-0)+f(0)=0\cdot x+0=0$$

Касательная в точке $x=1$:

$$y=3(x-1)+1=3x-3+1=3x-2$$

Шаг 3. Найдём точку пересечения графика и касательной

Решим уравнение:

$$3x-2=0\Rightarrow x=\frac{2}{3}$$

На отрезке от $x=0$ до $x=\frac{2}{3}$, график выше обеих касательных.
Но $y=0$ (касательная в $x=0$) совпадает с осью $Ox$, так что вклад от неё — ${\int }_0^1{x}^{3}dx$.

А $y=3x-2$ снизу пересекает график на $[2\mathrm{/}3;1]$, и её нужно вычесть.

Шаг 4. Составим выражение для площади

$$S={\int }_0^1{x}^{3}dx-{\int }_{2\mathrm{/}3}^1(3x-2)dx$$

Шаг 5. Найдём первообразные

$$\int x^{3}dx=\frac{x^4}{4},\int (3x-2)dx=\frac{3x^2}{2}-2x$$

Шаг 6. Вычислим оба интеграла

$${\int }_0^1{x}^{3}dx=\frac{1^4}{4}-0=\frac{1}{4}$$

$${\int }_{2\mathrm{/}3}^1(3x-2)dx=(\frac{3x^2}{2}-2x){\mid }_{2\mathrm{/}3}^1$$

Верхний предел ($x=1$):

$$\frac{3}{2}-2=-\frac{1}{2}$$

Нижний предел ($x=\frac{2}{3}$):

$$\frac{3}{2}\cdot \left(\frac{4}{9}\right)-2\cdot \frac{2}{3}=\frac{2}{3}-\frac{4}{3}=-\frac{2}{3}$$

Разность:

$$-\frac{1}{2}-(-\frac{2}{3})=-\frac{1}{2}+\frac{2}{3}=\frac{4-3}{6}=\frac{1}{6}$$

Шаг 7. Полная формула

$$S=\frac{1}{4}-\frac{1}{6}$$

Шаг 8. Приведение к общему знаменателю

$$\frac{1}{4}-\frac{1}{6}=\frac{3-2}{12}=\frac{1}{12}$$

Шаг 9. Ответ

Ответ: $\boxed{{\displaystyle \frac{1}{12}}}$