ГДЗ 10-11 Класс Номер 50.4 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

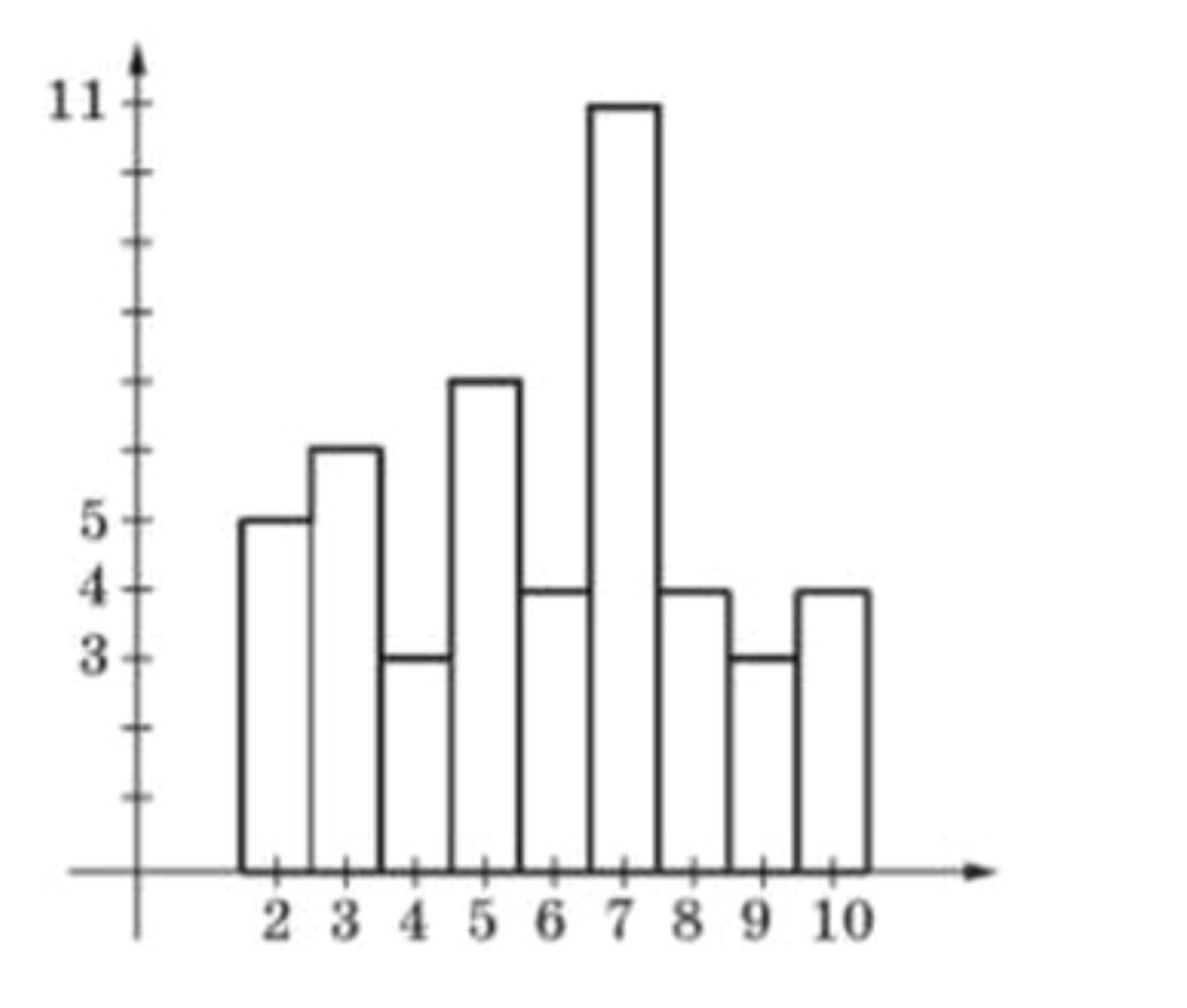
По приведённой гистограмме распределения данных (рис. 76) найдите:

а) количество вариант и объём измерения;

б) размах и моду измерения;

в) таблицу распределения данных;

г) среднее результатов измерения.

На рисунке 76 приведена гистограмма распределения данных;

а) Количество вариантов и объем измерения:
n = {2; 3; 4; 5; 6; 7; 8; 9} = 9 – вариант;
V = 5 + 6 + 3 + 7 + 4 + 11 + 4 + 3 + 4 = 47;

б) Размах и мода измерения:
R = xₘₐₓ — xₘᵢₙ = 11 — 3 = 8;
Mo = 7 (кратность равна 11);

в) Таблица распределения данных:

г) Среднее результатов измерения:

$$\bar{x}=\frac{2\cdot 5+3\cdot 6+4\cdot 3+5\cdot 7+6\cdot 4+7\cdot 11+8\cdot 4+9\cdot 3+10\cdot 4}{5+6+3+7+4+11+4+3+4};$$

$$\bar{x} = \frac{2 \cdot 5 + 3 \cdot 6 + 4 \cdot 3 + 5 \cdot 7 + 6 \cdot 4 + 7 \cdot 11 + 8 \cdot 4 + 9 \cdot 3 + 10 \cdot 4}{5 + 6 + 3 + 7 + 4 + 11 + 4 + 3 + 4};$$ $$\bar{x} = \frac{10 + 18 + 12 + 35 + 24 + 77 + 32 + 27 + 40}{47} = \frac{275}{47};$$

а) Количество вариант и объём измерения

1. Что такое варианта?
Варианта — это отдельное значение, которое принимает измеряемая величина.
По гистограмме определены следующие значения вариант:

$$\text{Варианты: } \{2; 3; 4; 5; 6; 7; 8; 9; 10\}$$

2. Количество вариант (n):
Это количество уникальных значений вариант. У нас:

$$n = 9$$

3. Объём измерения (V):
Это сумма всех кратностей (частот), т.е. общее количество наблюдений. Считаем по гистограмме:

$$V = 5 + 6 + 3 + 7 + 4 + 11 + 4 + 3 + 4$$

Считаем по действиям:

• $5 + 6 = 11$
• $11 + 3 = 14$
• $14 + 7 = 21$
• $21 + 4 = 25$
• $25 + 11 = 36$
• $36 + 4 = 40$
• $40 + 3 = 43$
• $43 + 4 = 47$

$$V = 47$$

Ответ (а):

• Количество вариант: $n = 9$
• Объём измерения: $V = 47$

б) Размах и мода измерения

1. Размах (R):
Размах — это разность между максимальной и минимальной вариантой:

• Минимальное значение: $x_{\text{min}} = 2$
• Максимальное значение: $x_{\text{max}} = 10$

$$R = x_{\text{max}} — x_{\text{min}} = 10 — 2 = 8$$

2. Мода (Mo):
Мода — это значение варианта, которое встречается наиболее часто, то есть с максимальной кратностью.
По данным:

• Значение 7 имеет кратность 11 — это наибольшее значение.

$$Mo = 7$$

Ответ (б):

• Размах: $R = 8$
• Мода: $Mo = 7$ (кратность равна 11)

в) Таблица распределения данных

Запишем полную таблицу вариант и соответствующих им кратностей (частот):

Пояснение:
Каждому значению варианта соответствует число, которое показывает, сколько раз оно встречается (по гистограмме). Например, значение 2 встречается 5 раз, значение 7 — 11 раз и т.д.

Ответ (в): Таблица указана выше.

г) Среднее результатов измерения

Формула для среднего арифметического (взвешенная средняя):

$$\bar{x} = \frac{\sum (x_i \cdot f_i)}{\sum f_i}$$

Где:

• $x_i$ — значения вариант;
• $f_i$ — соответствующие кратности (частоты);
• $\sum f_i = 47$ — объём измерения.

Подставим данные:

$$\bar{x} = \frac{ 2 \cdot 5 + 3 \cdot 6 + 4 \cdot 3 + 5 \cdot 7 + 6 \cdot 4 + 7 \cdot 11 + 8 \cdot 4 + 9 \cdot 3 + 10 \cdot 4 }{47}$$

Выполним все умножения:

• $2 \cdot 5 = 10$
• $3 \cdot 6 = 18$
• $4 \cdot 3 = 12$
• $5 \cdot 7 = 35$
• $6 \cdot 4 = 24$
• $7 \cdot 11 = 77$
• $8 \cdot 4 = 32$
• $9 \cdot 3 = 27$
• $10 \cdot 4 = 40$

Сложим числитель:

• $10 + 18 = 28$
• $28 + 12 = 40$
• $40 + 35 = 75$
• $75 + 24 = 99$
• $99 + 77 = 176$
• $176 + 32 = 208$
• $208 + 27 = 235$
• $235 + 40 = 275$

Теперь подставим:

$$\bar{x} = \frac{275}{47}$$

Можно разделить для получения приближённого значения:

$$\bar{x} \approx 5{,}851$$

Ответ (г):

• Среднее значение результатов измерения:

$$\bar{x}=\frac{275}{47}\approx \mathrm{5,851}$$$$\bar{x} = \frac{275}{47} \approx 5{,}851$$