ГДЗ 10-11 Класс Номер 50.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Ниже, в задачах 50.8 — 50.11, рассматриваются результаты, которые получили выпускники одной из школ на сочинении. Выставлялись две отметки: первая — по литературе, вторая — по русскому языку. Отметки эти таковы:

5/4 4/5 3/1 4/3 2/3 3/3 4/3 5/3 3/3 1/2

4/4 4/2 2/1 3/5 3/4 4/3 5/5 4/4 5/4 2/2

2/3 4/3 5/4 2/3 3/3

Для отметок по литературе:

а) выпишите сгруппированный ряд данных;

б) составьте таблицу распределения кратностей;

в) постройте многоугольник распределения процентных частот;

г) найдите среднее.

Даны отметки по литературе:
5, 4, 3, 4, 2, 3, 4, 5, 3, 1, 4, 4, 2, 3, 3, 4, 5, 4, 5, 2, 2, 4, 5, 2, 3;

а) Сгруппированный ряд данных:
1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5;

б) Таблица распределения кратностей:

в) Многоугольник распределения процентных частот:

$${\nu }_1=\frac{1}{25}\cdot 100\mathrm{\%}=4\mathrm{\%},{\nu }_2=\frac{5}{25}\cdot 100\mathrm{\%}=20\mathrm{\%};$$

$$\nu_1 = \frac{1}{25} \cdot 100\% = 4\%,\quad \nu_2 = \frac{5}{25} \cdot 100\% = 20\%;$$ $${\nu }_3=\frac{6}{25}\cdot 100\mathrm{\%}=24\mathrm{\%},{\nu }_4=\frac{8}{25}\cdot 100\mathrm{\%}=32\mathrm{\%};$$

$$\nu_3 = \frac{6}{25} \cdot 100\% = 24\%,\quad \nu_4 = \frac{8}{25} \cdot 100\% = 32\%;$$ $$\nu_5 = \frac{5}{25} \cdot 100\% = 20\%;$$

г) Среднее арифметическое:

$$\bar{x}=\frac{1\cdot 1+2\cdot 5+3\cdot 6+4\cdot 8+5\cdot 5}{1+5+6+8+5};$$

$$\bar{x} = \frac{1 \cdot 1 + 2 \cdot 5 + 3 \cdot 6 + 4 \cdot 8 + 5 \cdot 5}{1 + 5 + 6 + 8 + 5};$$ $$\bar{x} = \frac{1 + 10 + 18 + 32 + 25}{25} = \frac{86}{25} = 3{,}44;$$

Исходные данные:

Оценки:
5, 4, 3, 4, 2, 3, 4, 5, 3, 1, 4, 4, 2, 3, 3, 4, 5, 4, 5, 2, 2, 4, 5, 2, 3

а) Сгруппированный ряд данных

1. Выпишем оценки:

5 4 3 4 2 3 4 5 3 1 4 4 2 3 3 4 5 4 5 2 2 4 5 2 3

2. Отсортируем по возрастанию:

1, 2, 2, 2, 2, 2,
3, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 4, 4, 4,
5, 5, 5, 5, 5

Проверка:
Сумма количества: 1 + 5 + 6 + 8 + 5 = 25 — всё верно.

Ответ (а):
Сгруппированный ряд данных:
1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5

б) Таблица распределения кратностей

1. Считаем, сколько раз встречается каждая оценка:

• 1 — 1 раз
• 2 — 5 раз
• 3 — 6 раз
• 4 — 8 раз
• 5 — 5 раз

2. Составим таблицу:

в) Многоугольник распределения процентных частот

1. Формула процентной частоты:

$$\nu_i = \frac{n_i}{n} \cdot 100\%$$

где:

• $n_i$ — число учеников с этой оценкой
• $n = 25$

2. Подставим значения:

$$\nu_1 = \frac{1}{25} \cdot 100\% = 4\%$$ $$\nu_2 = \frac{5}{25} \cdot 100\% = 20\%$$ $$\nu_3 = \frac{6}{25} \cdot 100\% = 24\%$$ $$\nu_4 = \frac{8}{25} \cdot 100\% = 32\%$$ $$\nu_5 = \frac{5}{25} \cdot 100\% = 20\%$$

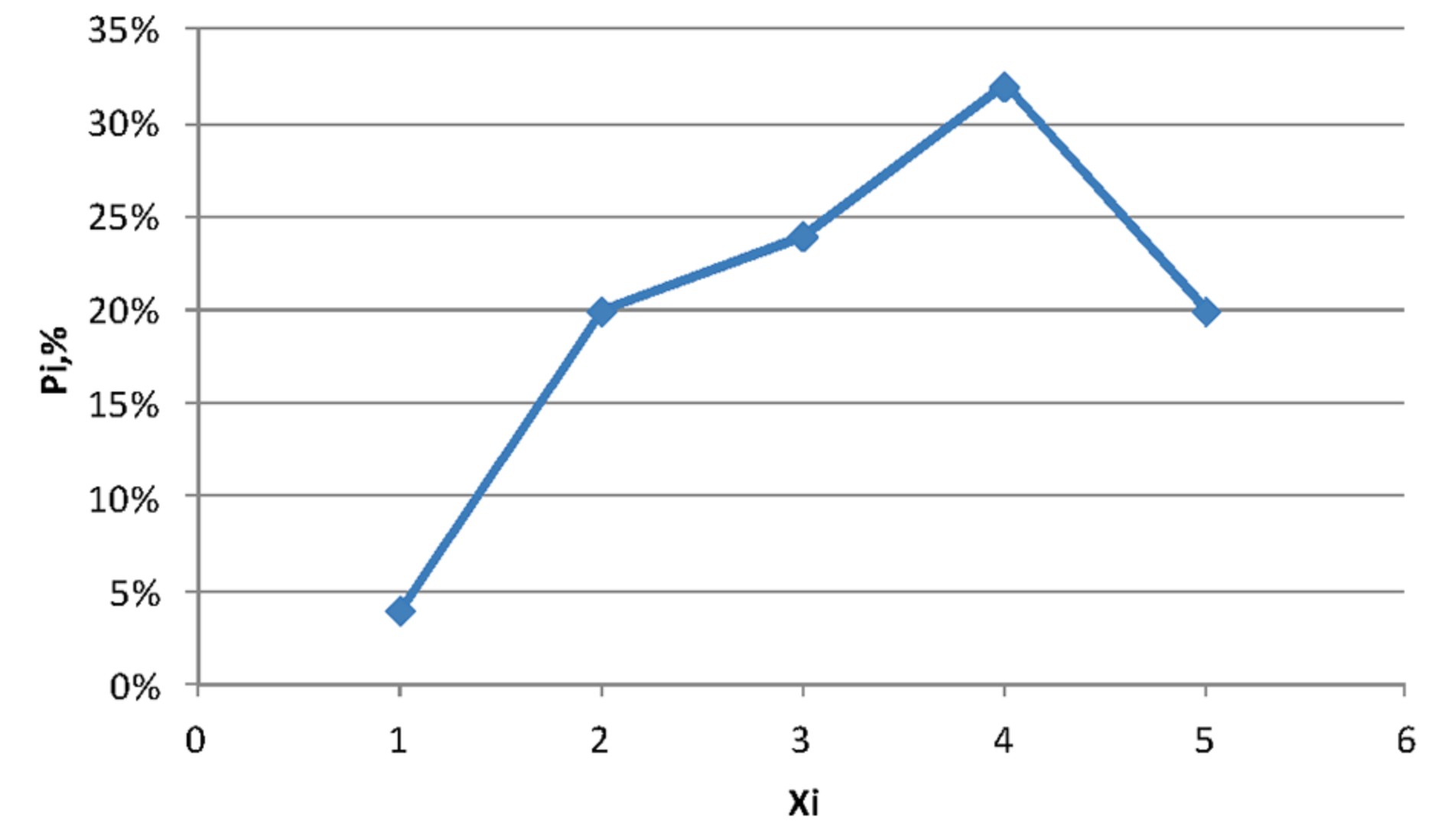
3. Точки многоугольника:

• (1, 4)
• (2, 20)
• (3, 24)
• (4, 32)
• (5, 20)

Описание многоугольника:

• Имеет один пик на значении 4 (32%)
• Почти симметричный: значения 2 и 5 имеют одинаковую частоту — 20%
• Оценка 1 встречается редко (4%)

г) Среднее арифметическое

1. Формула:

$$\bar{x} = \frac{1 \cdot n_1 + 2 \cdot n_2 + 3 \cdot n_3 + 4 \cdot n_4 + 5 \cdot n_5}{n}$$

Подставим:

$$\bar{x} = \frac{1 \cdot 1 + 2 \cdot 5 + 3 \cdot 6 + 4 \cdot 8 + 5 \cdot 5}{25}$$

2. Посчитаем числитель:

$$1 \cdot 1 = 1 \quad 2 \cdot 5 = 10 \quad 3 \cdot 6 = 18 \quad 4 \cdot 8 = 32 \quad 5 \cdot 5 = 25$$

Сумма:

$$1 + 10 + 18 + 32 + 25 = 86$$

3. Вычислим среднее:

$$\bar{x}=\frac{86}{25}=\mathrm{3,44}$$$$\bar{x} = \frac{86}{25} = 3{,}44$$