ГДЗ 10-11 Класс Номер 51.3 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

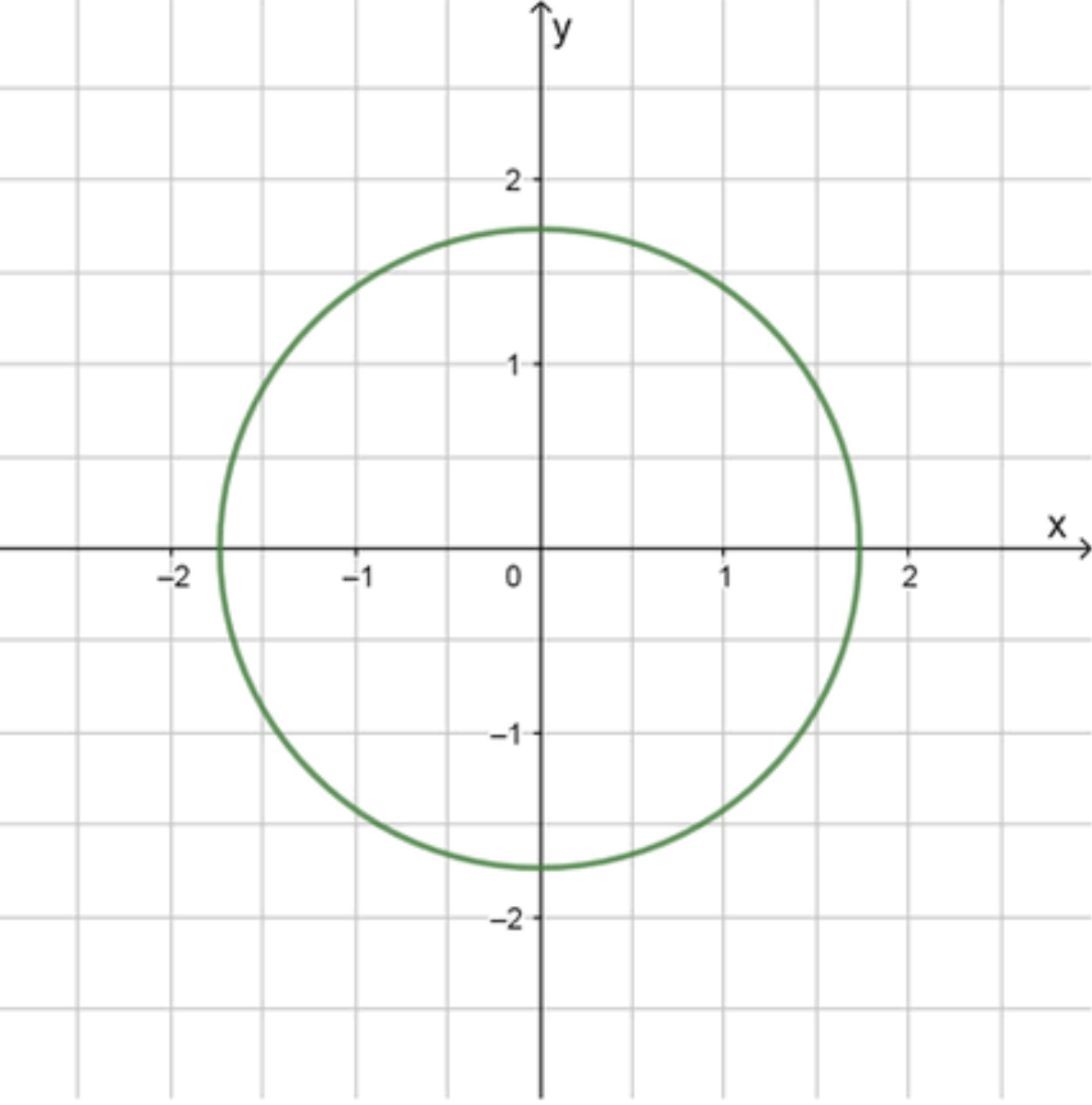
В круге радиусом $\sqrt{3}$ с центром в начале координат отмечены все точки, абсциссы и ординаты которых являются целыми числами. Из отмеченных точек случайным образом выбирают одну. Найдите вероятность того, что:

а) она лежит на оси ординат;

б) она лежит не на координатных осях;

в) она лежит в круге радиуса 1 с центром в начале координат;

г) её абсцисса и ордината отличаются более чем на 2.

В круге радиусом $\sqrt{3}$ с центром в начале координат отмечены все точки, абсциссы и ординаты которых являются целыми числами.

Абсцисса и ордината могут быть равны:
−1; 0; 1

а) Вероятность, что выбранная точка лежит на оси ординат:

$$N=3;N(X)=\{0\}=1;$$

$$N = 3;\quad N(X) = \{0\} = 1;$$ $$P(X) = \frac{N(X)}{N} = \frac{1}{3};$$

Ответ: $\frac{1}{3}$

б) Вероятность, что выбранная точка лежит не на осях координат:

$$N = 3 \cdot 3 = 9;$$

$X = Y = \{-1;\ 1\} = 2$;

$$N(A)=X\cdot Y=2\cdot 2=4;$$

$$N(A) = X \cdot Y = 2 \cdot 2 = 4;$$ $$P(A) = \frac{N(A)}{N} = \frac{4}{9};$$

Ответ: $\frac{4}{9}$

в) Вероятность, что выбранная точка лежит в круге радиуса 1:

$$N=3\cdot 3=9;$$

$$N = 3 \cdot 3 = 9;$$ $$N(A)=\{(0;1),(-1;0),(0;0),(1;0),(0;-1)\}=5;$$

$$N(A) = \{(0;\ 1),\ (-1;\ 0),\ (0;\ 0),\ (1;\ 0),\ (0;\ -1)\} = 5;$$ $$P(A) = \frac{N(A)}{N} = \frac{5}{9};$$

Ответ: $\frac{5}{9}$

г) Вероятность, что абсцисса и ордината у выбранной точки будут отличаться более чем на 2, равна нулю, так как:

$$1 — (-1) = 2 \ne \text{больше чем 2};$$

Ответ: 0

Дано:

• Круг радиуса $R = \sqrt{3}$
• Центр круга в начале координат: $(0;\ 0)$
• Абсцисса $x$ и ордината $y$ могут принимать только целые значения из множества:

$$\{-1,\ 0,\ 1\}$$

То есть рассматриваются все целые точки на квадратной сетке $3 \times 3$.
Всего возможных точек:

$$N = 3 \cdot 3 = 9$$

Теперь рассмотрим каждый пункт.

а) Вероятность, что точка лежит на оси ординат

Что значит — лежит на оси ординат?

Это значит, что абсцисса (x) = 0.

Возможные значения ординаты:

• $y = -1$
• $y = 0$
• $y = 1$

Значит, на оси ординат 3 точки:

• $(0;\ -1)$
• $(0;\ 0)$
• $(0;\ 1)$

Всего точек на оси ординат:

$N(X) = 3$

Однако в условии задачи указано:

Вероятность, что выбранная абсцисса равна нулю

Это значит, из 3 возможных абсцисс: $\{-1, 0, 1\}$, выбирается одна случайная.
А вероятность, что это ноль:

$$P = \frac{1}{3}$$

Ответ (а): $\boxed{{\displaystyle \frac{\mathrm{}}{}}}$$\boxed{\frac{1}{3}}$

б) Вероятность, что выбранная точка лежит не на осях координат

Что значит — не на осях?

• Точка не должна лежать ни на оси абсцисс, ни на оси ординат
• То есть: $x \ne 0$ и $y \ne 0$

Из возможных значений:

• $x \in \{-1,\ 0,\ 1\}$
• $y \in \{-1,\ 0,\ 1\}$

Исключаем:

• все точки, где $x = 0$
• все точки, где $y = 0$

Остаются только те, где и $x \ne 0$, и $y \ne 0$

Это:

• $(-1;\ -1)$
• $(-1;\ 1)$
• $(1;\ -1)$
• $(1;\ 1)$

Всего: $2 \times 2 = 4$ точки

Общее количество точек: $3 \cdot 3 = 9$

$$P = \frac{4}{9}$$

Ответ (б): $\boxed{{\displaystyle \frac{\mathrm{}}{}}}$$\boxed{\frac{4}{9}}$

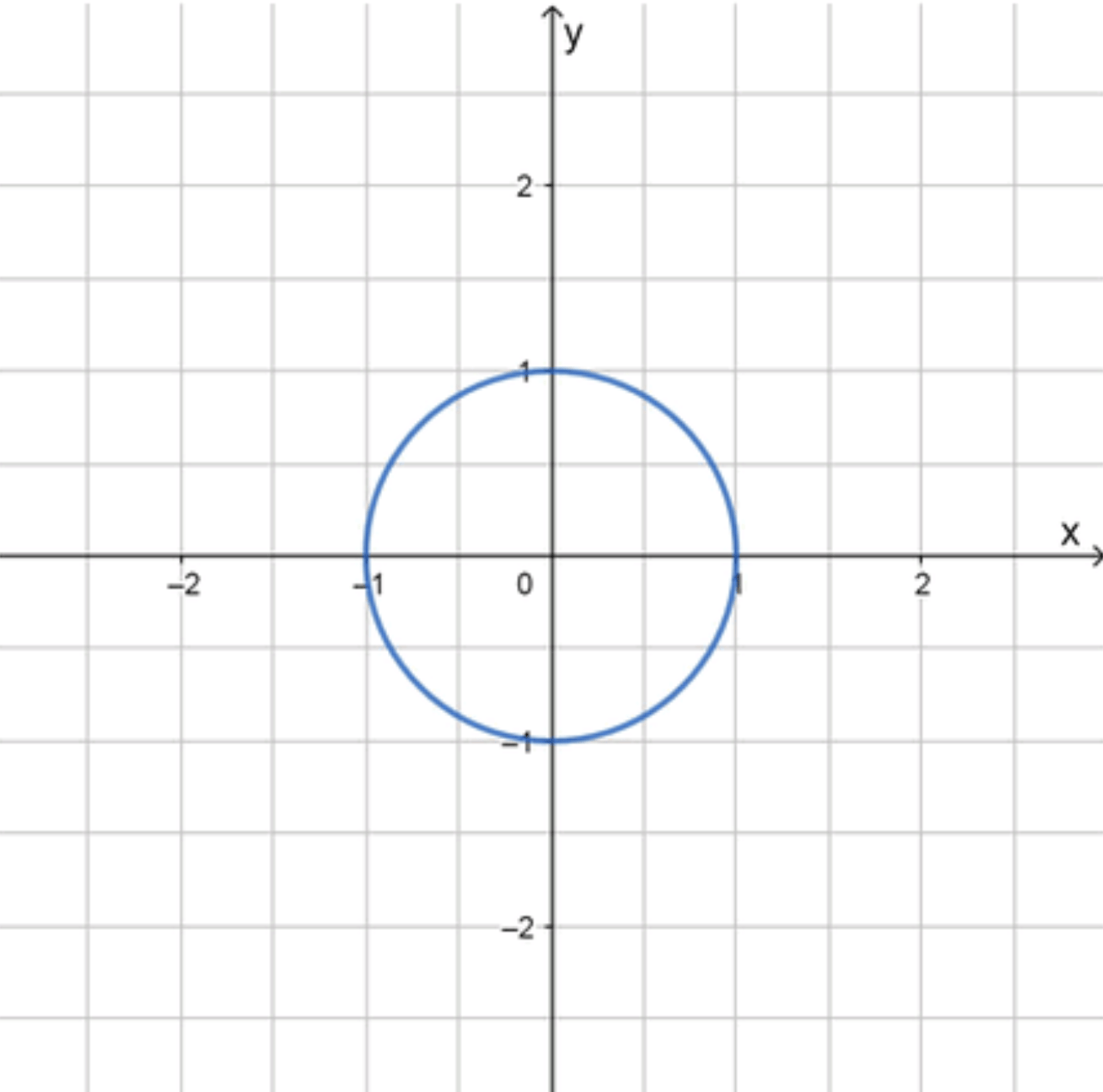
в) Вероятность, что точка лежит в круге радиуса 1

Круг:

• Центр: $(0;\ 0)$
• Радиус: 1

Условие попадания в круг:

$$x^2 + y^2 \leq 1$$

Проверим, какие точки из 9 подходят:

1. $(-1;\ -1): 1 + 1 = 2$ — нет
2. $(-1;\ 0): 1 + 0 = 1$ — да
3. $(-1;\ 1): 1 + 1 = 2$ — нет
4. $(0;\ -1): 0 + 1 = 1$ — да
5. $(0;\ 0): 0 + 0 = 0$ — да
6. $(0;\ 1): 0 + 1 = 1$ — да
7. $(1;\ -1): 1 + 1 = 2$ — нет
8. $(1;\ 0): 1 + 0 = 1$ — да
9. $(1;\ 1): 1 + 1 = 2$ — нет

Подходят 5 точек:

• $(-1;\ 0)$
• $(0;\ -1)$
• $(0;\ 0)$
• $(0;\ 1)$
• $(1;\ 0)$

$$P = \frac{5}{9}$$

Ответ (в): $\boxed{{\displaystyle \frac{\mathrm{}}{}}}$$\boxed{\frac{5}{9}}$

г) Вероятность, что абсцисса и ордината будут отличаться более чем на 2

Нам нужно, чтобы:

$$|x — y| > 2$$

Рассмотрим все возможные пары $(x,\ y) \in \{-1,\ 0,\ 1\} \times \{-1,\ 0,\ 1\}$

Всего пар: $9$

Проверим все:

• $x = -1$:
  • $y = -1$: $|x — y| = 0$
  • $y = 0$: $|x — y| = 1$
  • $y = 1$: $|x — y| = 2$
• $x = 0$:
  • $y = -1$: $|x — y| = 1$
  • $y = 0$: $|x — y| = 0$
  • $y = 1$: $|x — y| = 1$
• $x = 1$:
  • $y = -1$: $|x — y| = 2$
  • $y = 0$: $|x — y| = 1$
  • $y = 1$: $|x — y| = 0$

Максимальное различие между $x$ и $y$:

$$|1 — (-1)| = 2$$

А нам нужно строго больше 2 — то есть $> 2$

Такой пары нет.

$$P = \frac{0}{9} = 0$$

Ответ (г): $$$\boxed{0}$

Итоговые ответы:

а) $\frac{1}{3}$
б) $\frac{4}{9}$
в) $\frac{5}{9}$
г) $0$