ГДЗ 10-11 Класс Номер 54.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

В прямоугольнике ABCD со сторонами АВ = 2, ВС = 5 случайно выбирают точку. Найдите вероятность того, что она расположена:

а) ближе к прямой АВ, чем к прямой CD;

б) ближе к вершине А, чем к вершине С;

в) ближе к прямой АВ, чем к прямой ВС;

г) ближе к вершине А, чем к точке пересечения диагоналей.

В прямоугольнике ABCD со сторонами $AB = 2$, $BC = 5$ случайно выбирают точку.

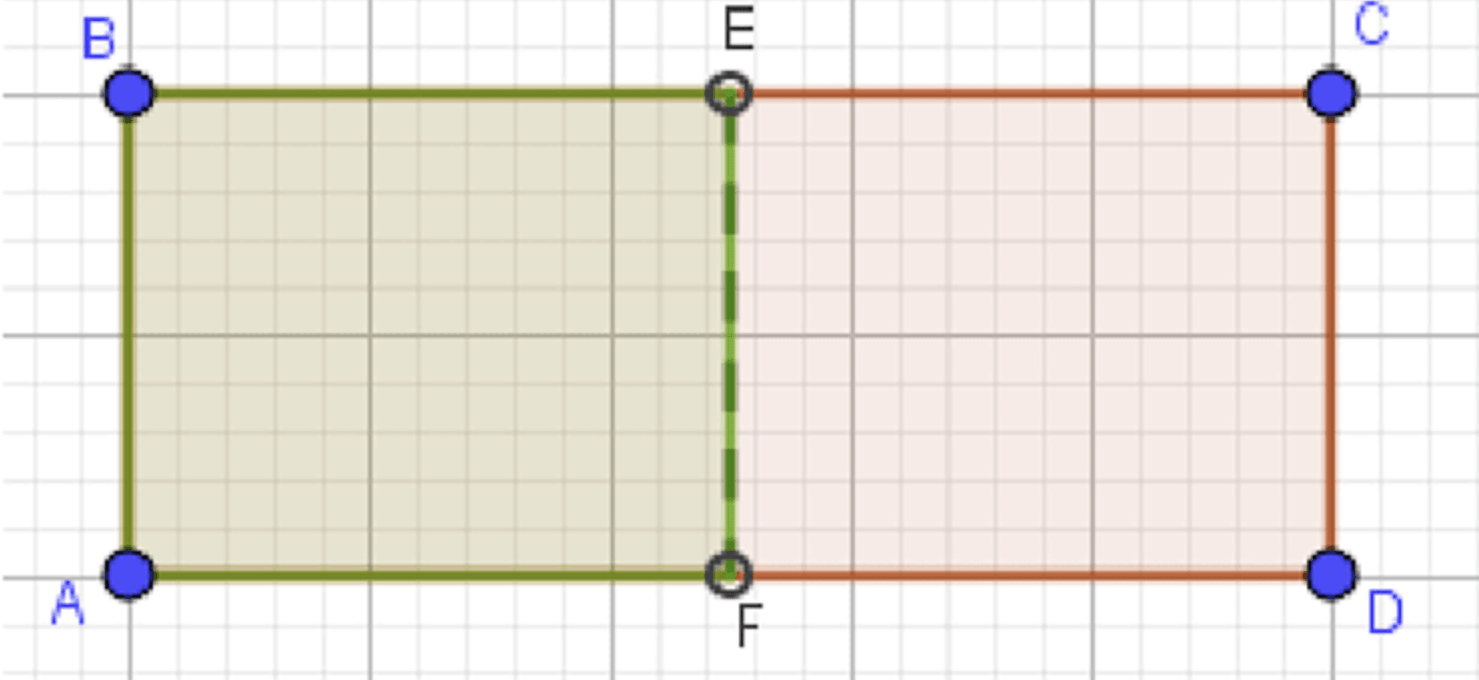
а) Вероятность, что она лежит ближе к прямой AB, чем к прямой CD:

Подходящая точка лежит внутри прямоугольника $ABEE_1$:

$$P = \frac{S_{ABEE_1}}{S_{ABCD}} = \frac{AB \cdot BE}{AB \cdot BC} = \frac{BE}{BC} = \frac{BC}{2} : BC = \frac{1}{2} = 0{,}5$$

Ответ: 0,5.

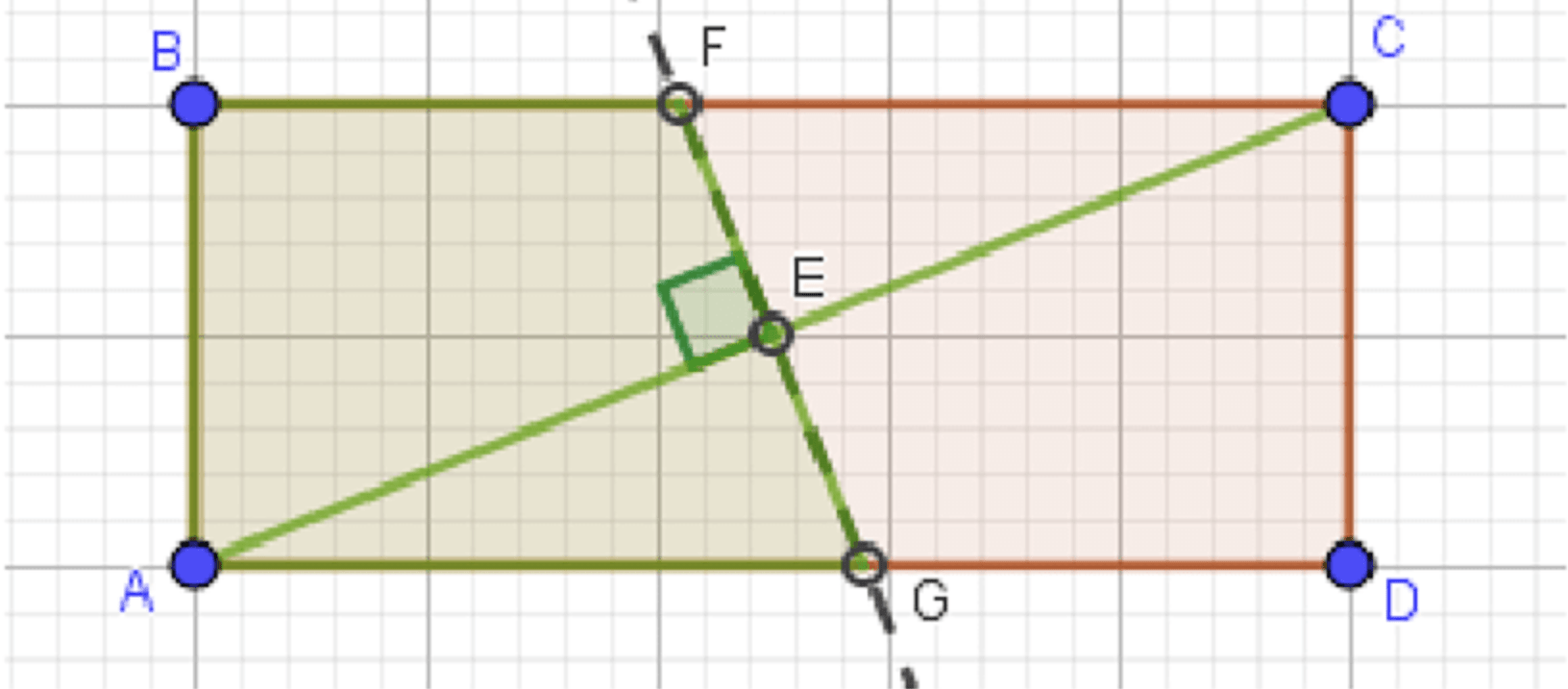
б) Вероятность, что она лежит ближе к вершине A, чем к вершине C:

Рассмотрим прямоугольные треугольники $AOE_1$ и $COE$:
$AO = OC$, $\angle OAE_1 = \angle OCE$;
$\triangle AOE_1 = \triangle COE$;
$EC = AE_1$;

Подходящая точка лежит внутри трапеции $ABEE_1$:

$$P = \frac{S_{ABEE_1}}{S_{ABCD}} = \frac{\frac{1}{2} AB \cdot (BE + AE_1)}{AB \cdot BC} = \frac{1}{2} \cdot \frac{(BE + AE)}{BC} = \frac{1}{2} \cdot \frac{BC}{BC} = 0{,}5$$

Ответ: 0,5.

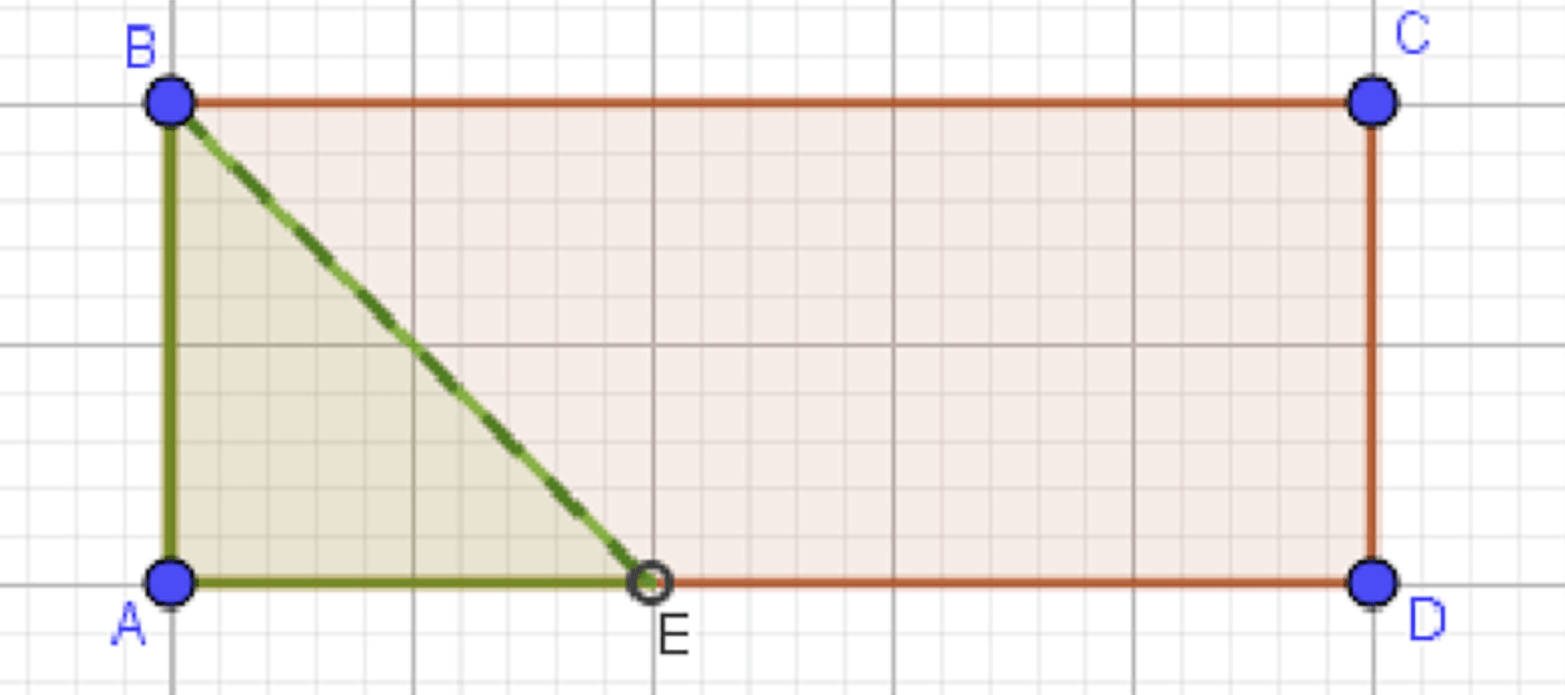
в) Вероятность, что она лежит ближе к прямой AB, чем к прямой BC:

Рассмотрим прямоугольный треугольник $BAE$:
$\angle ABE = 45^\circ$;
$AE = AB = 2$;

Подходящая точка лежит внутри треугольника $ABE$:

$$P = \frac{S_{ABE}}{S_{ABCD}} = \frac{\frac{1}{2} AB \cdot AE}{AB \cdot BC} = \frac{1}{2} \cdot \frac{AB}{BC} = \frac{1}{2} \cdot \frac{2}{5} = \frac{1}{5} = 0{,}2$$

Ответ: 0,2.

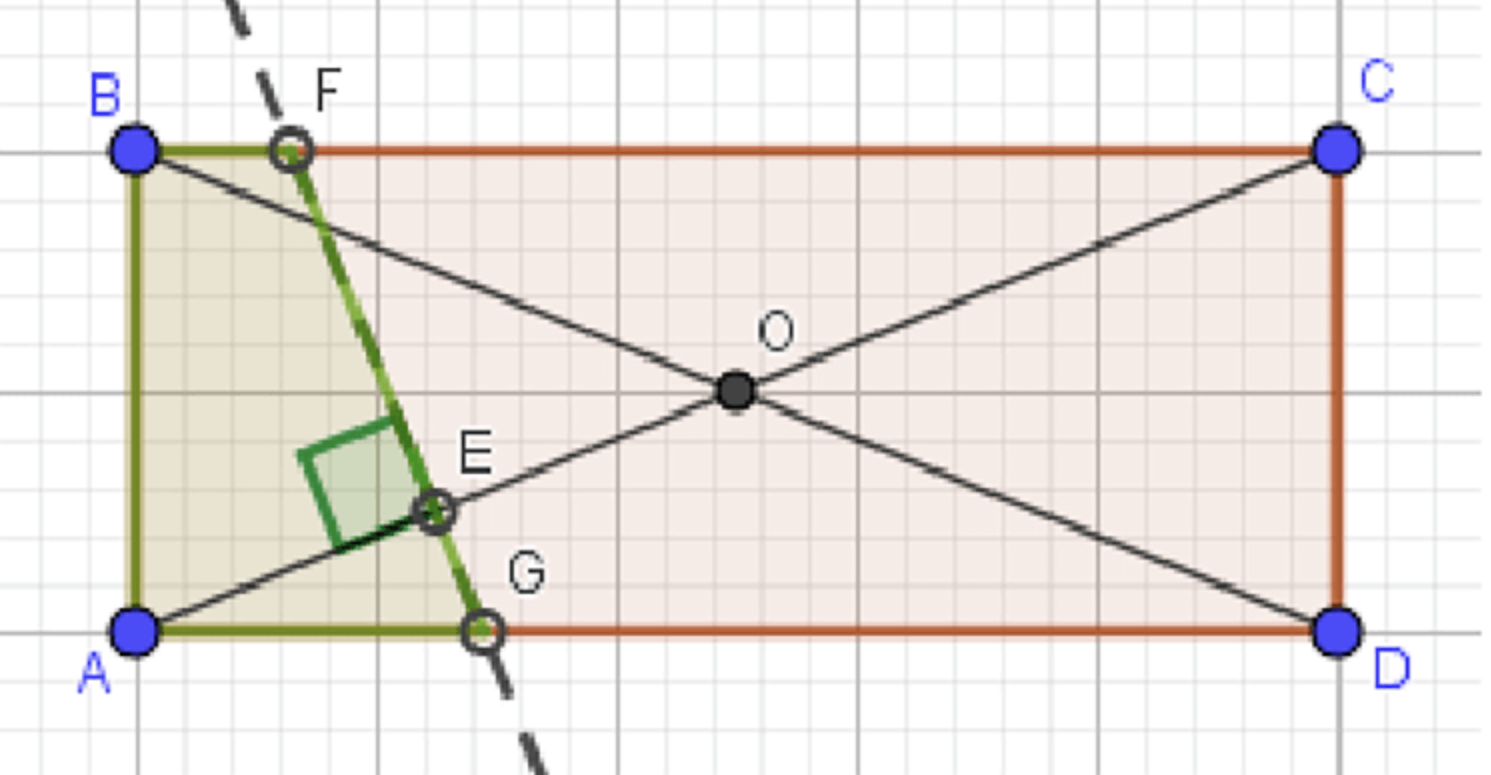
г) Вероятность, что она лежит ближе к вершине A, чем к точке O:

$$A{O}_1=O_{1}O=\frac{1}{2}\cdot \frac{1}{2}\cdot AC=\frac{1}{4}AC;$$

$$AO_1 = O_1O = \frac{1}{2} \cdot \frac{1}{2} \cdot AC = \frac{1}{4} AC; \quad O_1C = OO_1 + OC = \frac{1}{4} AC + \frac{1}{2} AC = \frac{3}{4} AC$$

Рассмотрим прямоугольные треугольники $EO_1C$ и $ABC$:
$\angle ECO_1 = \angle ACB$;
$\triangle EO_1C \sim \triangle ABC$;

$$\frac{BC}{O_{1}C}=\frac{AC}{EC};EC=\frac{O_{1}C\cdot AC}{BC}=\frac{\frac{3}{4}AC\cdot AC}{BC}=\frac{3}{4}\cdot \frac{A{C}^2}{BC}=\frac{3}{4}\cdot \frac{A{B}^2+B{C}^2}{BC}$$

$$\frac{BC}{O_1C} = \frac{AC}{EC}; \quad EC = \frac{O_1C \cdot AC}{BC} = \frac{\frac{3}{4} AC \cdot AC}{BC} = \frac{3}{4} \cdot \frac{AC^2}{BC} = \frac{3}{4} \cdot \frac{AB^2 + BC^2}{BC}$$ $$EC=\frac{3}{4}\cdot \frac{2^2+5^2}{5}=\frac{3}{4}\cdot \frac{4+25}{5}=\frac{3}{4}\cdot \frac{29}{5}=\frac{87}{20}$$

$$EC = \frac{3}{4} \cdot \frac{2^2 + 5^2}{5} = \frac{3}{4} \cdot \frac{4 + 25}{5} = \frac{3}{4} \cdot \frac{29}{5} = \frac{87}{20}$$ $$BE = BC — EC = 5 — \frac{87}{20} = \frac{13}{20}$$

Рассмотрим прямоугольные треугольники $EO_1C$ и $E_1O_1A$:
$\angle O_1AE_1 = \angle O_1CE$;
$\triangle EO_1C \sim \triangle E_1O_1A$;

$$\frac{EC}{AE_1} = \frac{O_1C}{AO_1} = \frac{\frac{3}{4} AC}{\frac{1}{4} AC} = 3; \quad AE_1 = \frac{1}{3} EC = \frac{1}{3} \cdot \frac{87}{20} = \frac{29}{20}$$

Подходящая точка лежит внутри трапеции $ABEE_1$:

$$P = \frac{S_{ABEE_1}}{S_{ABCD}} = \frac{\frac{1}{2} AB \cdot (BE + AE_1)}{AB \cdot BC} = \frac{1}{2 \cdot 5} \cdot \left( \frac{13}{20} + \frac{29}{20} \right) = \frac{1}{10} \cdot \frac{42}{20} = \frac{42}{200} = 0{,}21$$

Ответ: 0,21.

Пусть ABCD — прямоугольник с вершинами по порядку $A(0, 0), B(2, 0), C(2, 5), D(0, 5)$.
Сторона $AB = 2$, сторона $BC = 5$.
Случайная точка выбирается равномерно внутри прямоугольника.

Требуется найти вероятности в четырёх случаях.

а) Вероятность, что точка расположена ближе к прямой AB, чем к прямой CD

Прямые AB и CD — горизонтальные стороны прямоугольника.
AB — нижняя сторона, CD — верхняя.
Расстояние между прямыми AB и CD: 5 (высота прямоугольника).

Чтобы точка была ближе к AB, чем к CD, её расстояние до AB должно быть меньше, чем расстояние до CD.

Расстояние от произвольной точки $(x, y)$ до прямой AB (то есть до оси $y = 0$) — это просто $y$.
Расстояние до прямой CD (то есть до оси $y = 5$) — это $5 — y$.

Итак, условие:

$$y < 5 — y \Rightarrow 2y < 5 \Rightarrow y < \frac{5}{2}$$

То есть точка должна находиться ниже середины прямоугольника по вертикали.

Область подходящих точек — это нижняя половина прямоугольника (от $y = 0$ до $y = \frac{5}{2}$).

Площадь всей фигуры:

$$S_{ABCD} = AB \cdot BC = 2 \cdot 5 = 10$$

Площадь нижней половины:

$$S = AB \cdot \frac{BC}{2} = 2 \cdot \frac{5}{2} = 5$$

Искомая вероятность:

$$P = \frac{5}{10} = \frac{1}{2} = 0{,}5$$

Ответ: 0,5

б) Вероятность, что точка расположена ближе к вершине A, чем к вершине C

Координаты точек:

• $A(0, 0)$
• $C(2, 5)$

Пусть $P(x, y)$ — случайная точка в прямоугольнике.
Рассмотрим расстояния:

• $PA^2 = (x — 0)^2 + (y — 0)^2 = x^2 + y^2$
• $PC^2 = (x — 2)^2 + (y — 5)^2 = (x — 2)^2 + (y — 5)^2$

Требуется:

$$x^2 + y^2 < (x — 2)^2 + (y — 5)^2$$

Вычислим правую часть:

$$(x — 2)^2 = x^2 — 4x + 4, \quad (y — 5)^2 = y^2 — 10y + 25$$ $$(x — 2)^2 + (y — 5)^2 = x^2 + y^2 — 4x -10y + 29$$

Подставим в неравенство:

$$x^2+y^2<x^2+y^2-4x-10y+29\Rightarrow 0<-4x-10y+29\Rightarrow$$

$$x^2 + y^2 < x^2 + y^2 — 4x — 10y + 29 \Rightarrow 0 < -4x -10y + 29 \Rightarrow 4x + 10y < 29$$

Это уравнение прямой. Выражаем:

$$y < \frac{29 — 4x}{10}$$

Это прямая, делящая прямоугольник на две части: ниже — точка ближе к A, выше — к C.

Найдем площадь фигуры под этой прямой внутри прямоугольника:

1. При $x = 0$: $y < \frac{29 — 0}{10} = 2.9$
2. При $x = 2$: $y < \frac{29 — 8}{10} = 2.1$

Получается, в прямоугольнике проведена прямая от точки $(0, 2.9)$ до $(2, 2.1)$.

Область ниже этой прямой — трапеция с основаниями:

• $y_1 = 2.9$, $y_2 = 2.1$, ширина по $x = 2$

Площадь трапеции:

$$S = \frac{1}{2} \cdot (2.9 + 2.1) \cdot 2 = \frac{1}{2} \cdot 5 \cdot 2 = 5$$

(подтверждает, что прямая делит прямоугольник пополам)

Искомая вероятность:

$$P = \frac{5}{10} = 0{,}5$$

Ответ: 0,5

в) Вероятность, что точка расположена ближе к прямой AB, чем к прямой BC

AB — нижняя сторона, горизонтальная прямая
BC — правая сторона, вертикальная прямая

Координаты сторон:

• AB: $y = 0$
• BC: $x = 2$

Пусть точка $(x, y)$.
Расстояние до AB: $y$
Расстояние до BC: $2 — x$

Условие:

$$y < 2 — x \Rightarrow x + y < 2$$

Это уравнение прямой, делящей прямоугольник по диагонали от $(0, 2)$ до $(2, 0)$

Область подходящих точек — под этой диагональю: треугольник с вершинами $A(0,0), B(2,0), E(0,2)$

Площадь треугольника:

$$S = \frac{1}{2} \cdot 2 \cdot 2 = 2$$

Площадь прямоугольника: 10

$$P = \frac{2}{10} = \frac{1}{5} = 0{,}2$$

Ответ: 0,2

г) Вероятность, что точка ближе к вершине A, чем к точке O — пересечению диагоналей

Координаты:

• $A(0, 0)$
• $C(2, 5)$
• Центр прямоугольника (точка пересечения диагоналей):

$$O = \left( \frac{0 + 2}{2}, \frac{0 + 5}{2} \right) = (1, 2.5)$$

Пусть точка $(x, y)$.
Рассмотрим расстояния:

• $PA^2 = x^2 + y^2$
• $PO^2 = (x — 1)^2 + (y — 2.5)^2$

Условие:

$$x^2 + y^2 < (x — 1)^2 + (y — 2.5)^2$$

Вычислим правую часть:

$$(x — 1)^2 = x^2 — 2x + 1, \quad (y — 2.5)^2 = y^2 — 5y + 6.25$$ $$PO^2 = x^2 + y^2 — 2x — 5y + 7.25$$

Подставим:

$$x^2+y^2<x^2+y^2-2x-5y+7.25\Rightarrow 0<-2x-5y+7.25\Rightarrow$$

$$x^2 + y^2 < x^2 + y^2 — 2x — 5y + 7.25 \Rightarrow 0 < -2x -5y + 7.25 \Rightarrow 2x + 5y < 7.25$$

Имеем уравнение прямой:

$$y < \frac{7.25 — 2x}{5}$$

Найдем точки пересечения этой прямой с границами прямоугольника:

При $x = 0$:

$$y = \frac{7.25 — 0}{5} = 1.45$$

При $x = 2$:

$$y = \frac{7.25 — 4}{5} = \frac{3.25}{5} = 0.65$$

Имеем трапецию с высотой 2 (от $x = 0$ до $x = 2$), и основаниями $1.45$ и $0.65$.

Площадь трапеции:

$$S = \frac{1}{2} \cdot (1.45 + 0.65) \cdot 2 = \frac{1}{2} \cdot 2.1 \cdot 2 = 2.1$$

Площадь прямоугольника: 10

Искомая вероятность:

$$P = \frac{2.1}{10} = 0.21$$

Ответ: 0,21