ГДЗ 10-11 Класс Номер 54.24 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Произвольно выбирают числа $x$ и $y$ так, что $|x| \leq 1$ и $|y| \leq 1$. Точку $(x,\ y)$ отмечают на координатной плоскости. Какова вероятность того, что:

а) эта точка лежит в первой координатной четверти;

б) $x + y < 0$;

в) эта точка лежит или во второй, или в четвёртой координатной четверти;

г) $x + y > 0$, а $xy < 0$?

Произвольно выбирают числа $x$ и $y$ так, что $|x| \leq 1$ и $|y| \leq 1$;

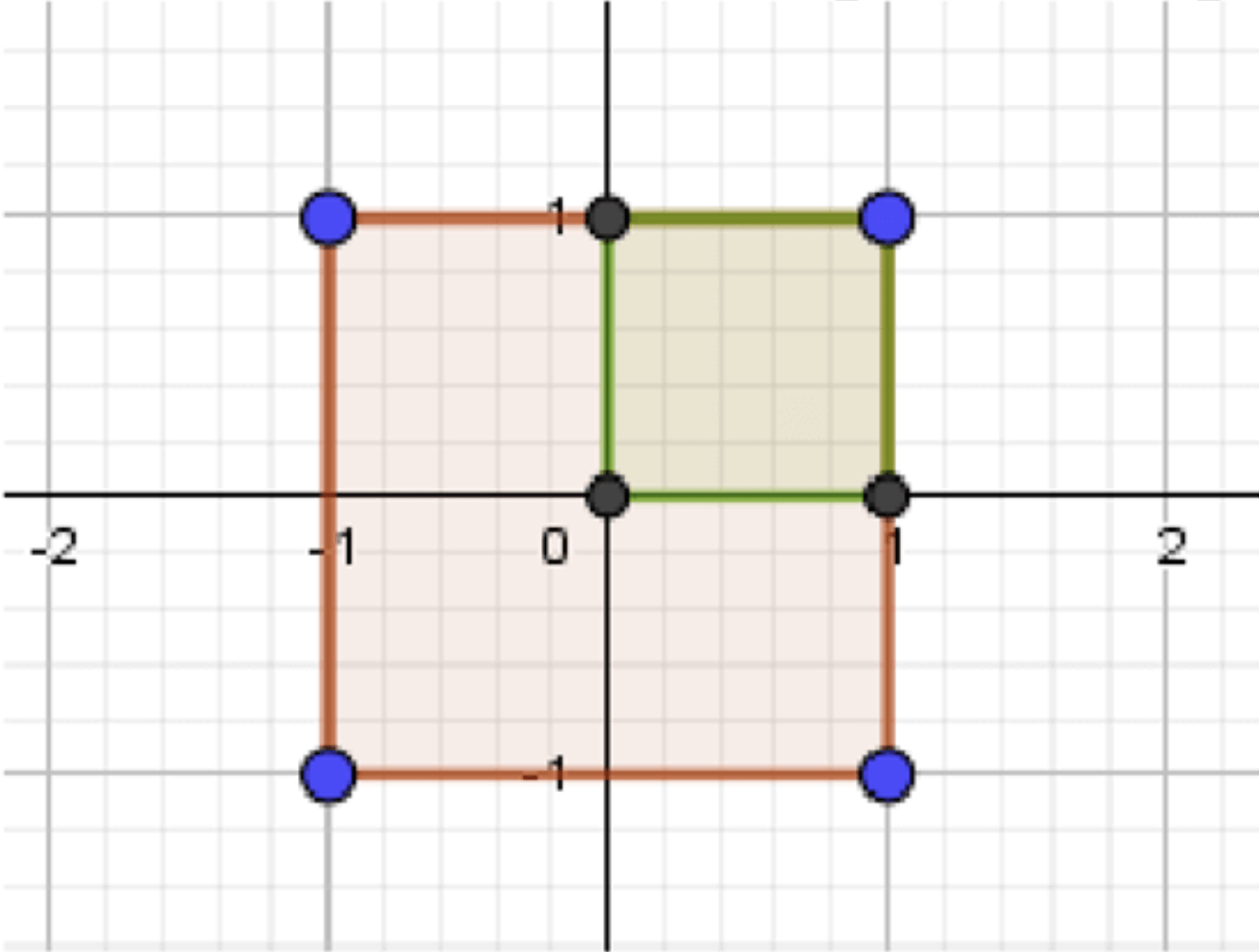
а) Вероятность, что эта точка лежит в первой четверти:

$$0\le x\le 1,0\le y\le 1;$$$$0 \leq x \leq 1,\quad 0 \leq y \leq 1;$$

Искомая точка лежит внутри квадрата $OECF$:

$$P = \frac{S_{OECF}}{S_{ABCD}} = \frac{(1 — 0)^2}{(1 — (-1))^2} = \frac{1^2}{2^2} = \frac{1}{4} = 0{,}25;$$

Ответ: 0,25.

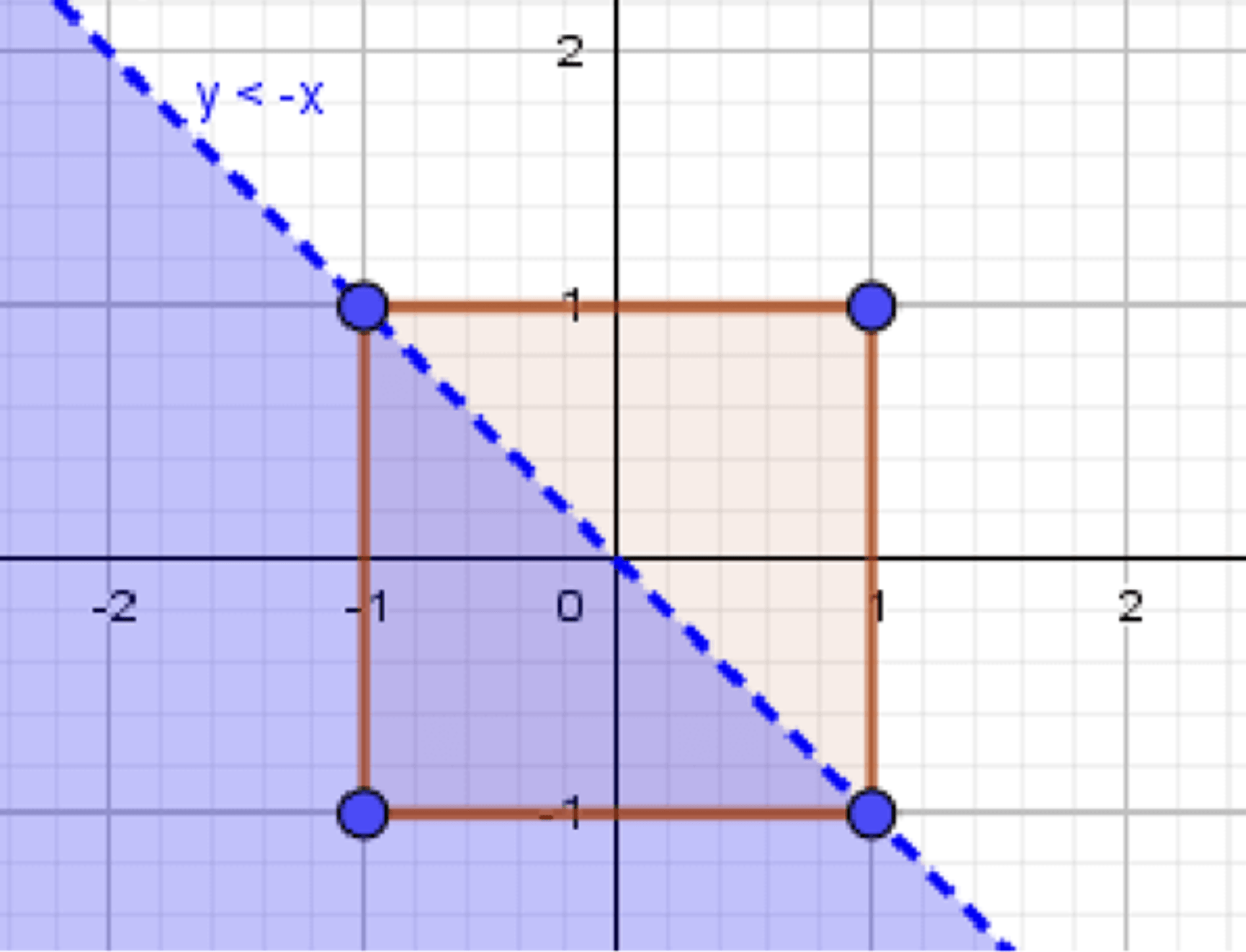
б) Вероятность, что выполняется неравенство:

$$x + y < 0;\quad \text{то есть } y < -x;$$

Искомая точка лежит внутри прямоугольного треугольника $\triangle BAD$:

$$P = \frac{S_{BAD}}{S_{ABCD}} = \frac{1}{2} \cdot \frac{(1 — (-1)) \cdot (1 — (-1))}{(1 — (-1))^2} = \frac{1}{2} = 0{,}5;$$

Ответ: 0,5.

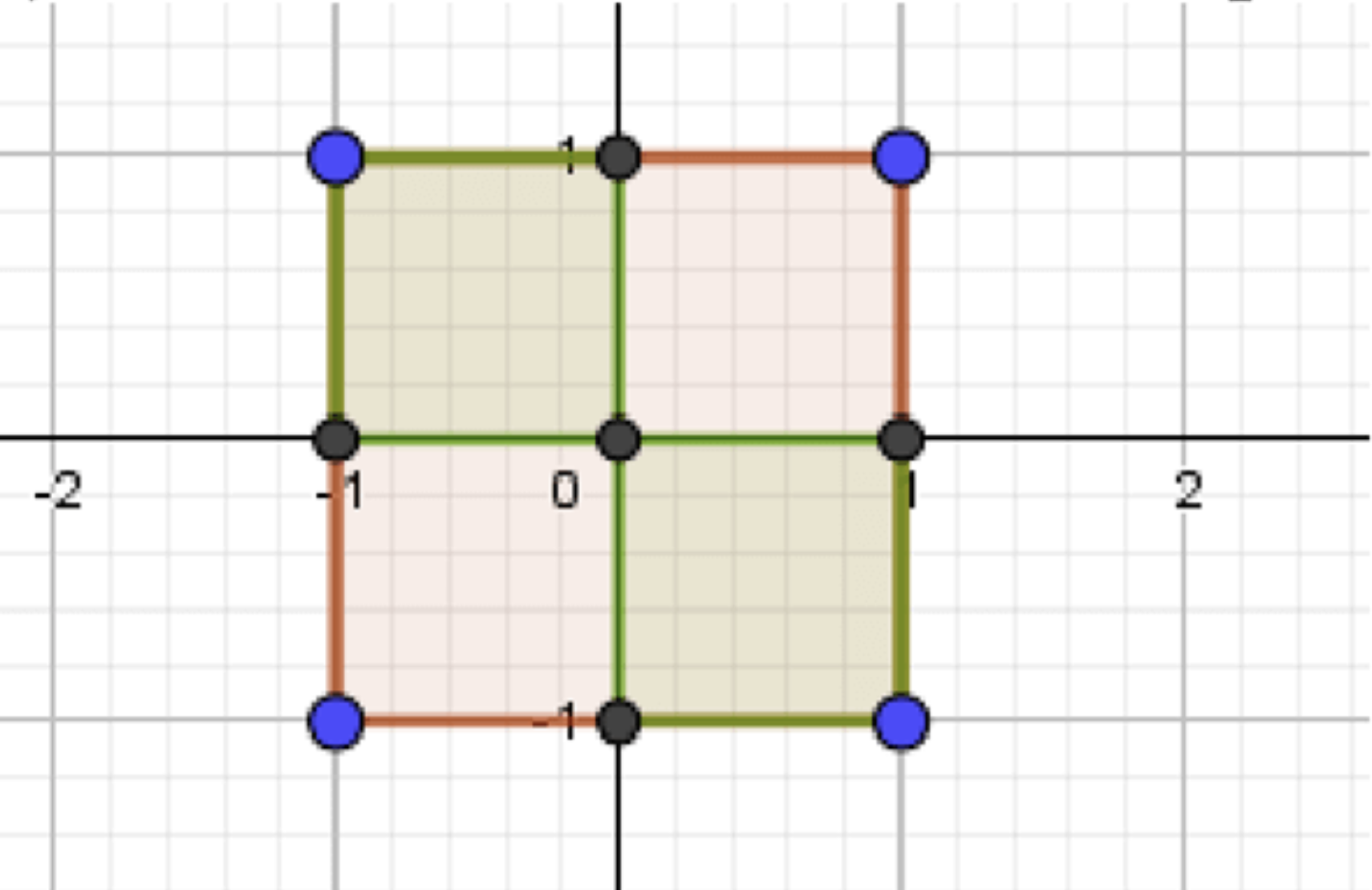
в) Вероятность, что эта точка лежит во II или IV четверти:

$$\left\{ \begin{aligned} -1 \leq x \leq 0 \\ 0 \leq y \leq 1 \end{aligned} \right. \quad \text{или} \quad \left\{ \begin{aligned} 0 \leq x \leq 1 \\ -1 \leq y \leq 0 \end{aligned} \right.$$

Искомая точка лежит внутри квадрата $FBEO$ или $E_1OF_1D$:

$$P = \frac{S_{FBEO} + S_{E_1OF_1D}}{S_{ABCD}} = \frac{(1 — 0)^2 + (1 — 0)^2}{(1 — (-1))^2} = \frac{1 + 1}{4} = \frac{2}{4} = 0{,}5;$$

Ответ: 0,5.

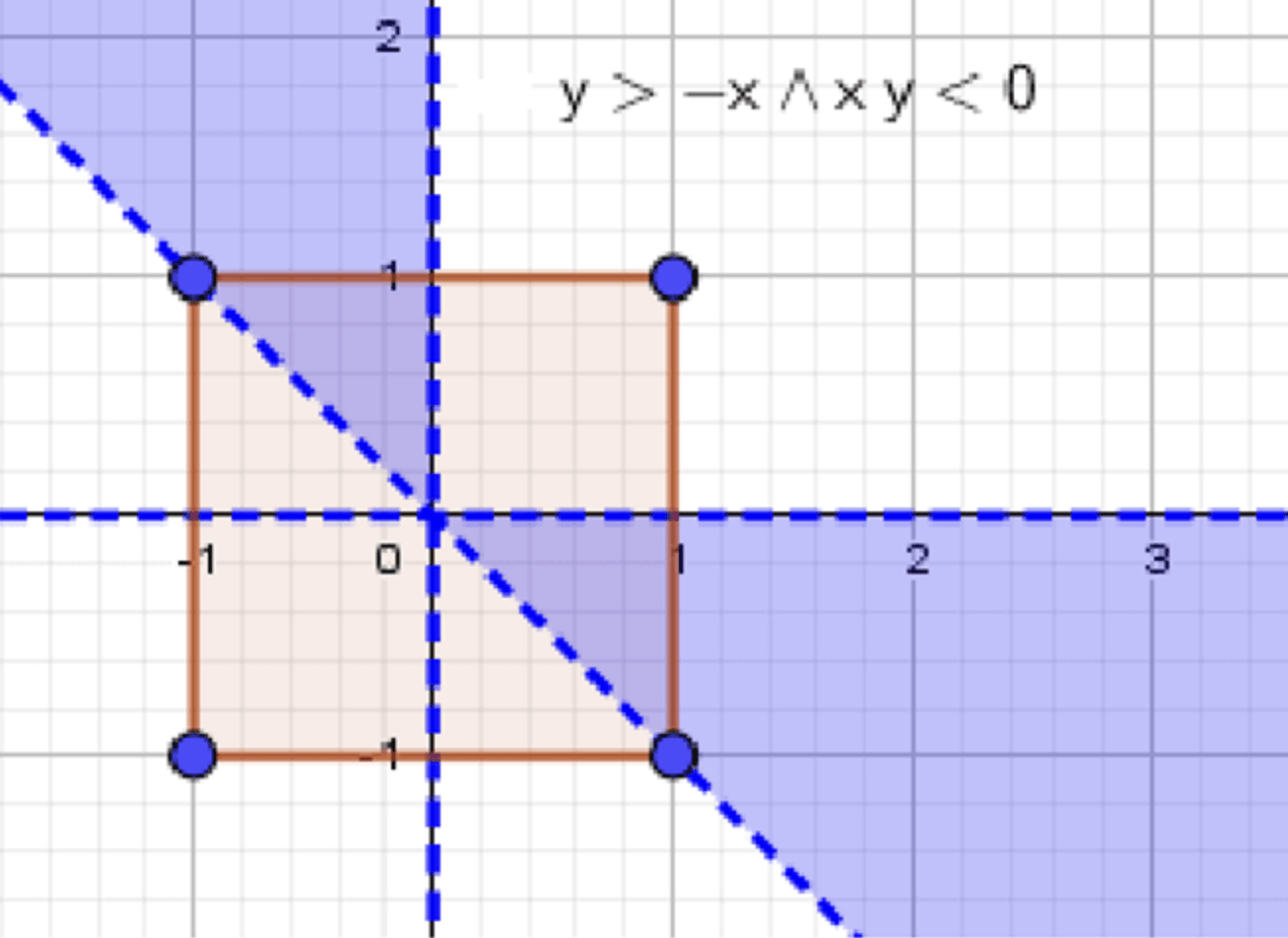
г) Вероятность, что выполняются неравенства:

$$\left\{ \begin{aligned} x + y > 0 \\ xy < 0 \end{aligned} \right. \quad \Rightarrow \quad \left\{ \begin{aligned} y > -x \\ xy < 0 \end{aligned} \right.$$

Искомая точка лежит внутри прямоугольного треугольника $\triangle BEO$ или $\triangle DFO$:

$$P = \frac{S_{BEO} + S_{DFO}}{S_{ABCD}} = \frac{\frac{1}{2} \cdot (1 — 0)^2 + \frac{1}{2} \cdot (1 — 0)^2}{(1 — (-1))^2} = \frac{1}{4} = 0{,}25;$$

Ответ: 0,25.

Произвольно выбирают числа $x$ и $y$ так, что

$$|x| \leq 1 \quad \text{и} \quad |y| \leq 1.$$

Это значит, что точка $(x, y)$ выбирается случайным образом в квадрате с вершинами:

• $A(-1, -1)$,
• $B(1, -1)$,
• $C(1, 1)$,
• $D(-1, 1)$.

Площадь всего квадрата $S_{\text{всего}} = 2 \times 2 = 4$.

а) Вероятность, что точка лежит в первой координатной четверти

Условие первой четверти:

$$x \in [0, 1],\quad y \in [0, 1]$$

Это квадрат со стороной 1, его площадь:

$$S = 1 \times 1 = 1$$

Вероятность попасть в первую четверть:

$$P = \frac{S_{\text{четверть}}}{S_{\text{всего}}} = \frac{1}{4} = 0{,}25$$

Ответ: 0,25

б) Вероятность, что $x + y < 0$

Уравнение прямой:

$$x + y = 0 \quad \Leftrightarrow \quad y = -x$$

Разделяет квадрат по диагонали: верхняя часть — $x + y > 0$, нижняя — $x + y < 0$

Треугольник под диагональю — равнобедренный, прямоугольный, с катетами 2.

$$S_{\text{ниже}} = \frac{1}{2} \cdot 2 \cdot 2 = 2$$ $$P = \frac{2}{4} = 0{,}5$$

Ответ: 0,5

в) Вероятность, что точка во II или IV четверти

II четверть:

$$x \in [-1, 0],\quad y \in [0, 1]$$

IV четверть:

$$x \in [0, 1],\quad y \in [-1, 0]$$

Каждая из этих областей — квадрат $1 \times 1$, площадь каждой: 1
Суммарная площадь:

$$S = 1 + 1 = 2$$ $$P = \frac{2}{4} = 0{,}5$$

Ответ: 0,5

г) Вероятность, что $x + y > 0$ и $xy < 0$

Разберем каждое условие:

1. $x + y > 0 \Rightarrow y > -x$
2. $xy < 0$ — произведение отрицательно ⇒ $x$ и $y$ разных знаков.

Возможны два случая:

• $x > 0$, $y < 0$
• $x < 0$, $y > 0$

Итак:

Случай 1: $x > 0, y < 0,$ и $x + y > 0 \Rightarrow y > -x$

Рассмотрим прямоугольный треугольник в четвертой четверти под прямой $y = -x$.
Вершины:

• $O(0, 0)$,
• $B(1, 0)$,
• $E(1, -1)$

Нас интересует область выше прямой $y = -x$, но при этом $y < 0$.
Это треугольник с вершинами $O(0, 0)$, $B(1, 0)$, $E(1, -1)$, выше прямой $y = -x$ — его площадь:

$$S_1 = \frac{1}{2} \cdot 1 \cdot 1 = \frac{1}{2}$$

Случай 2: $x < 0, y > 0,$ и $x + y > 0 \Rightarrow y > -x$

Рассматриваем треугольник в второй четверти, выше прямой $y = -x$.
Вершины:

• $O(0, 0)$,
• $D(-1, 0)$,
• $F(-1, 1)$

Опять нас интересует часть выше прямой $y = -x$, при $x < 0, y > 0$.
Площадь аналогична:

$$S_2 = \frac{1}{2} \cdot 1 \cdot 1 = \frac{1}{2}$$

Общая площадь:

$$S = \frac{1}{2} + \frac{1}{2} = 1$$ $$P = \frac{1}{4} = 0{,}25$$

Ответ: 0,25

Итоговые ответы:

а) 0,25
б) 0,5
в) 0,5
г) 0,25