Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 56.21 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите уравнение, используя функционально-графические методы:
а) \( x = \sqrt[3]{x} \)
б) \( |x| = \sqrt[5]{x} \)
Решить уравнение, используя функционально-графические методы:
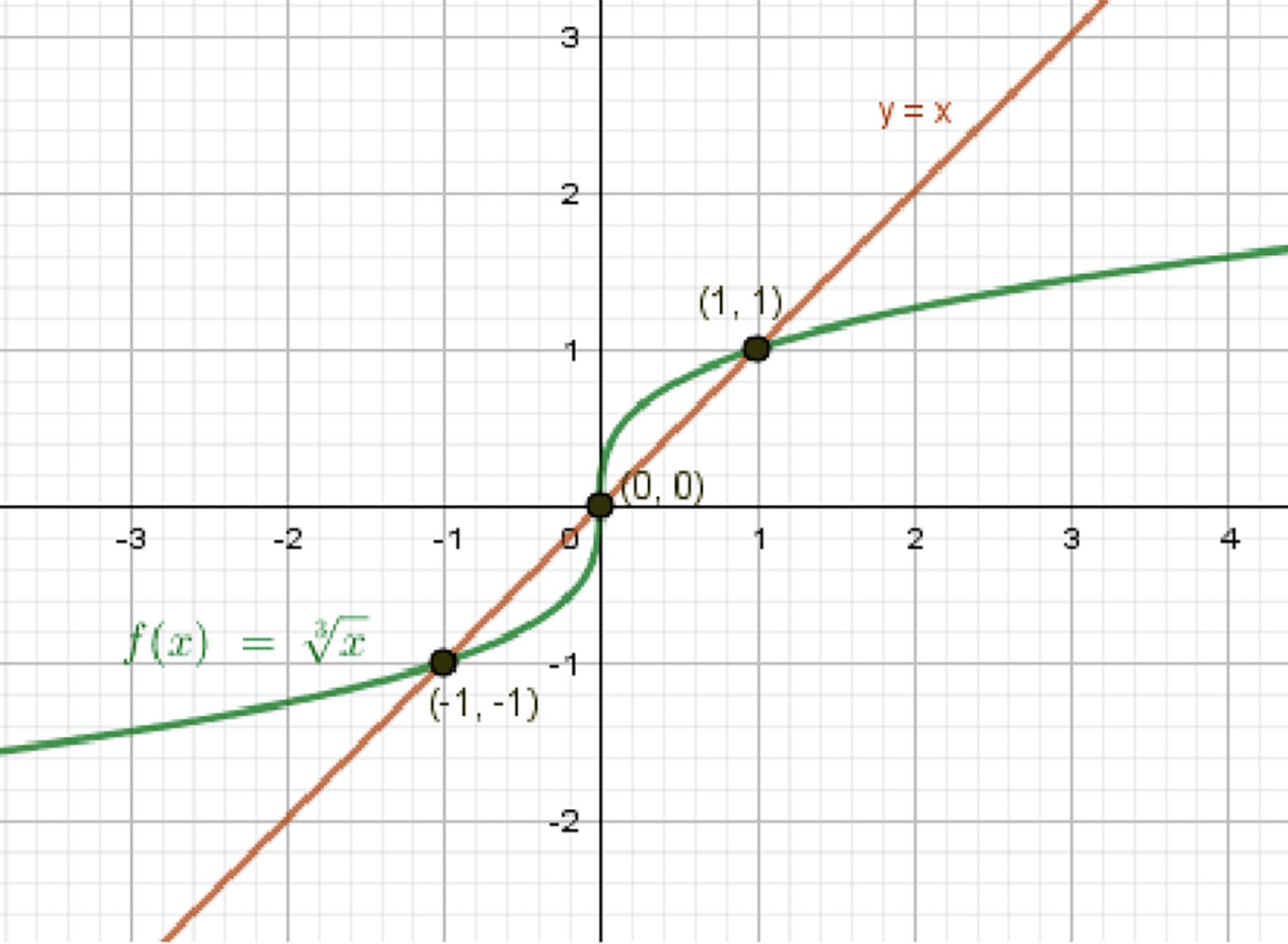
а) \( x = \sqrt[3]{x} \)
Функция \( y = x \) — уравнение прямой:
| \( x \) | 0 | 2 |
|---|---|---|
| \( y \) | 0 | 2 |
Функция \( y = \sqrt[3]{x} \) — кубическая парабола:
Точка пересечения: \( x_0 = 0 \), \( y_0 = 0 \)
| \( x \) | 1 | 8 |
|---|---|---|
| \( y \) | 1 | 2 |
Графики функций:
Ответ: \( x_1 = \pm 1 \); \( x_2 = 0 \)
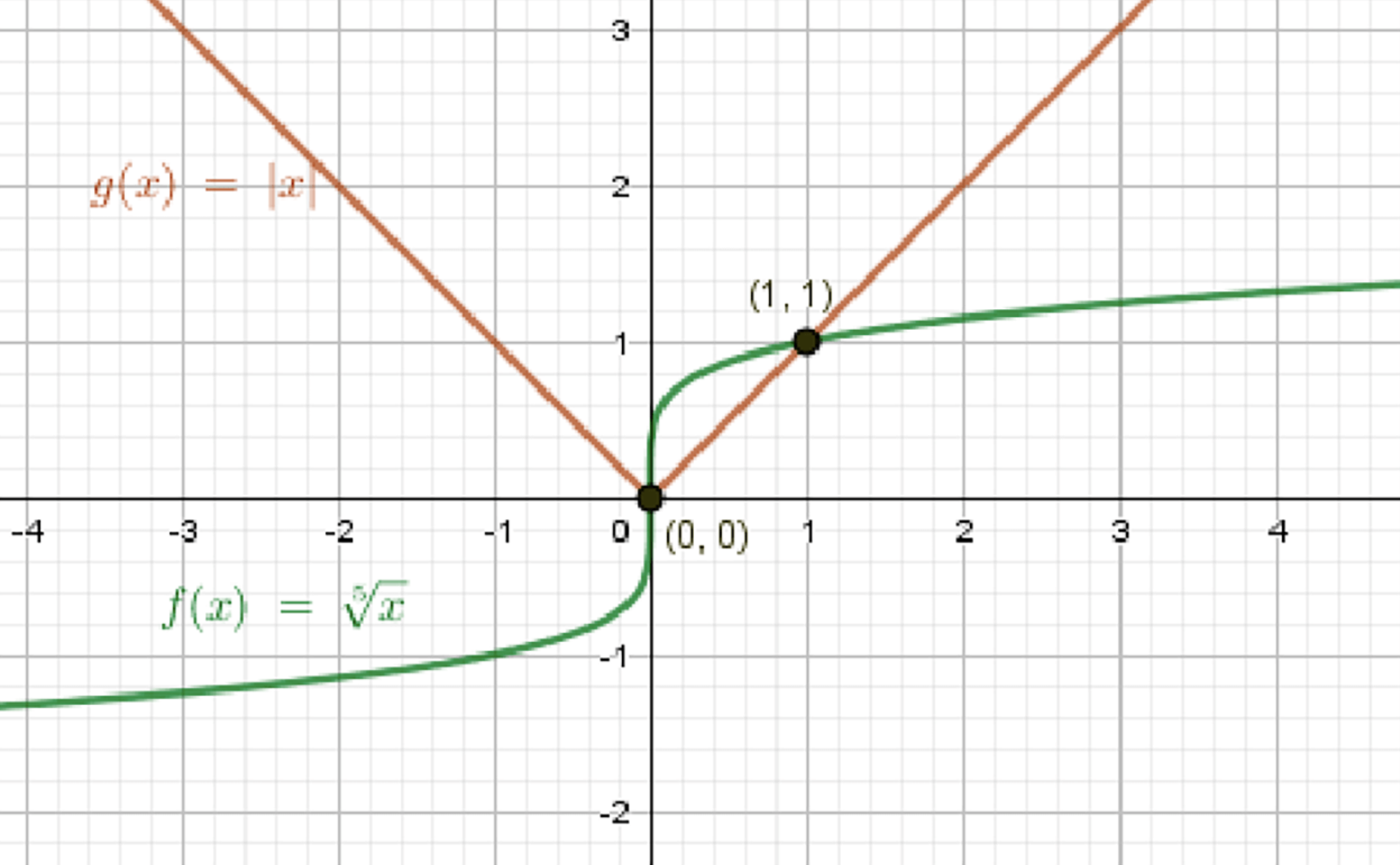
б) \( |x| = \sqrt[5]{x} \)
Функция \( y = |x| \) — уравнение ломаной:
Точка пересечения: \( x_0 = 0 \), \( y_0 = 0 \)
| \( x \) | -2 | 2 |
|---|---|---|
| \( y \) | 2 | 2 |
Функция \( y = \sqrt[5]{x} \) — пятая корневая кривая:
Точка пересечения: \( x_0 = 0 \), \( y_0 = 0 \)
| \( x \) | 1 | 32 |
|---|---|---|
| \( y \) | 1 | 2 |
Графики функций:
Ответ: \( x_1 = 0 \); \( x_2 = 1 \)
а) \( x = \sqrt[3]{x} \)
Рассмотрим графики левой и правой части уравнения:
1. График функции \( y = x \) — это прямая, проходящая через начало координат и все точки, где значение аргумента равно значению функции. То есть:
- Проходит через точку \( (0, 0) \)
- При \( x = 2 \), \( y = 2 \)
- График симметричен относительно прямой \( y = x \)
2. График функции \( y = \sqrt[3]{x} \) — это кубическая корневая функция. Она определена при всех значениях \( x \) и проходит через точку \( (0, 0) \), а также:
- При \( x = 1 \), \( y = \sqrt[3]{1} = 1 \)
- При \( x = 8 \), \( y = \sqrt[3]{8} = 2 \)
- При \( x = -1 \), \( y = \sqrt[3]{-1} = -1 \)
- График монотонно возрастает, не имеет разрывов и симметричен относительно начала координат (т.к. нечетная функция)
Ищем точки пересечения графиков функций \( y = x \) и \( y = \sqrt[3]{x} \). Такие точки удовлетворяют уравнению:
\( x = \sqrt[3]{x} \)
Чтобы найти корни, рассмотрим уравнение:
\( x = \sqrt[3]{x} \Rightarrow x — \sqrt[3]{x} = 0 \Rightarrow \sqrt[3]{x} (x^{\frac{2}{3}} — 1) = 0 \)
Решения:
- \( \sqrt[3]{x} = 0 \Rightarrow x = 0 \)
- \( x^{\frac{2}{3}} = 1 \Rightarrow x = \pm 1 \)
Ответ: \( x_1 = -1; \ x_2 = 0; \ x_3 = 1 \)
б) \( |x| = \sqrt[5]{x} \)
Рассмотрим графики левой и правой части уравнения:
1. График функции \( y = |x| \) — это V-образная ломаная:
- При \( x = 0 \), \( y = 0 \)
- Для \( x > 0 \): график совпадает с прямой \( y = x \)
- Для \( x < 0 \): график — прямая \( y = -x \)
- При \( x = -2 \), \( y = 2 \); при \( x = 2 \), \( y = 2 \)
2. График функции \( y = \sqrt[5]{x} \) — это пятая корневая функция:
- Функция определена при всех \( x \in \mathbb{R} \)
- Проходит через точку \( (0, 0) \)
- При \( x = 1 \), \( y = \sqrt[5]{1} = 1 \)
- При \( x = 32 \), \( y = \sqrt[5]{32} = 2 \)
- При \( x = -1 \), \( y = \sqrt[5]{-1} = -1 \)
- График монотонно возрастает и симметричен относительно начала координат (нечетная функция)
Чтобы найти точки пересечения, приравниваем функции:
\( |x| = \sqrt[5]{x} \)
Рассмотрим два случая:
Случай 1: \( x \ge 0 \Rightarrow |x| = x \)
Получаем уравнение: \( x = \sqrt[5]{x} \)
Решаем: \( x = \sqrt[5]{x} \Rightarrow x^{\frac{4}{5}} = 1 \Rightarrow x = 1 \)
Случай 2: \( x < 0 \Rightarrow |x| = -x \)
Получаем: \( -x = \sqrt[5]{x} \)
Но правая часть \( \sqrt[5]{x} \) при \( x < 0 \) — отрицательна, а левая \( -x \) — положительна, противоречие.
Следовательно, решений в области \( x < 0 \) нет, кроме:
\( x = 0 \): обе части равны нулю.
Ответ: \( x_1 = 0; \ x_2 = 1 \)