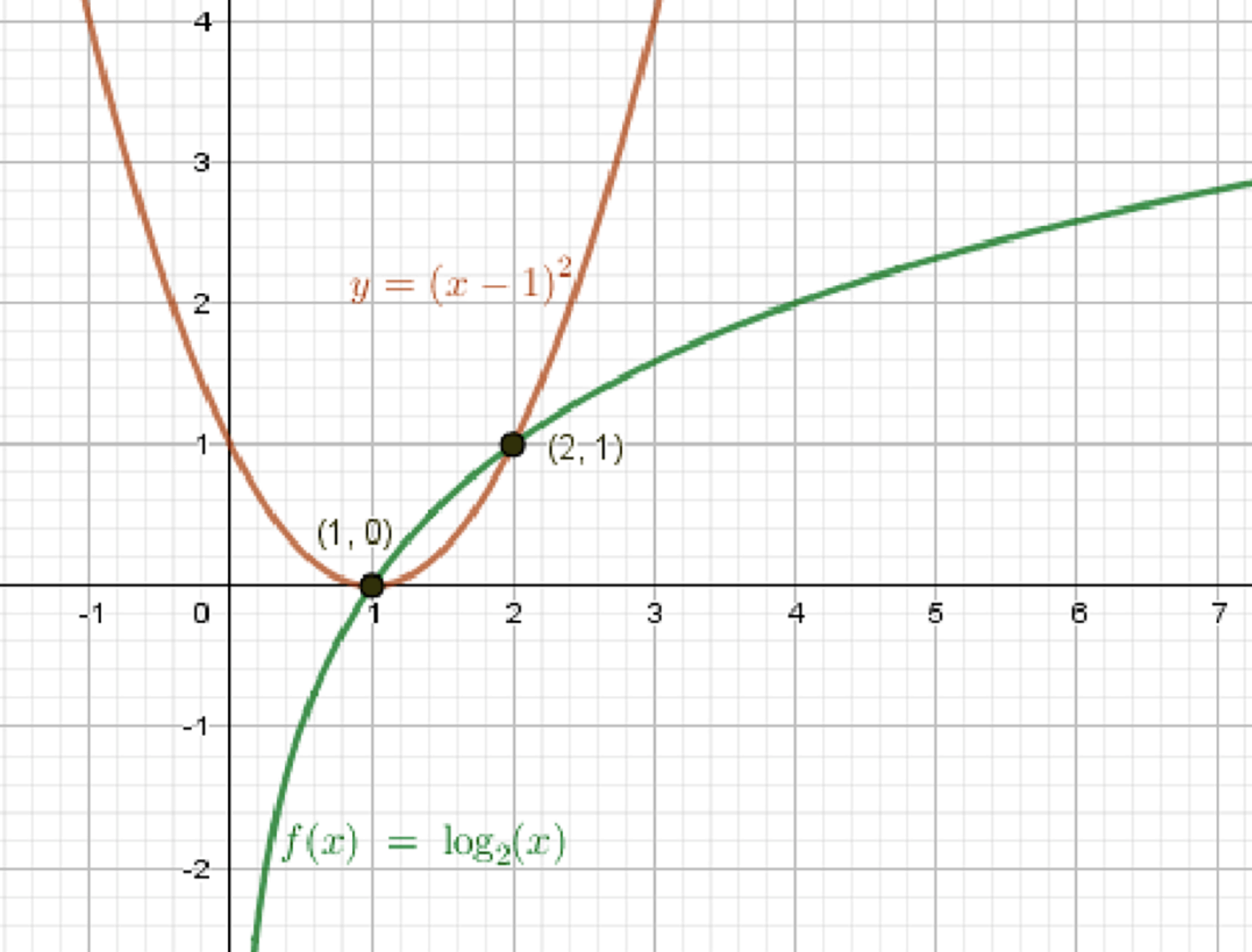Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 56.23 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( (x — 1)^2 = \log_2 x \)
б) \( \log_{\frac{1}{2}} x = \left( x + \frac{1}{2} \right)^2 \)
Решить уравнение, используя функционально-графические методы:
а) \( (x — 1)^2 = \log_2 x \)
\( y = (x — 1)^2 \) — уравнение параболы:
\( x_0 = 1 \), \( y_0 = 0 \)
| \( x \) | 2 | 3 | 4 |
|---|---|---|---|
| \( y \) | 1 | 4 | 9 |
\( y = \log_2 x \) — уравнение логарифмической функции:
| \( x \) | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| \( y \) | 0 | 1 | 2 | 3 |
Графики функций:
Ответ: \( x_1 = 1 \); \( x_2 = 2 \)
б) \( \log_{\frac{1}{2}} x = \left( x + \frac{1}{2} \right)^2 \)
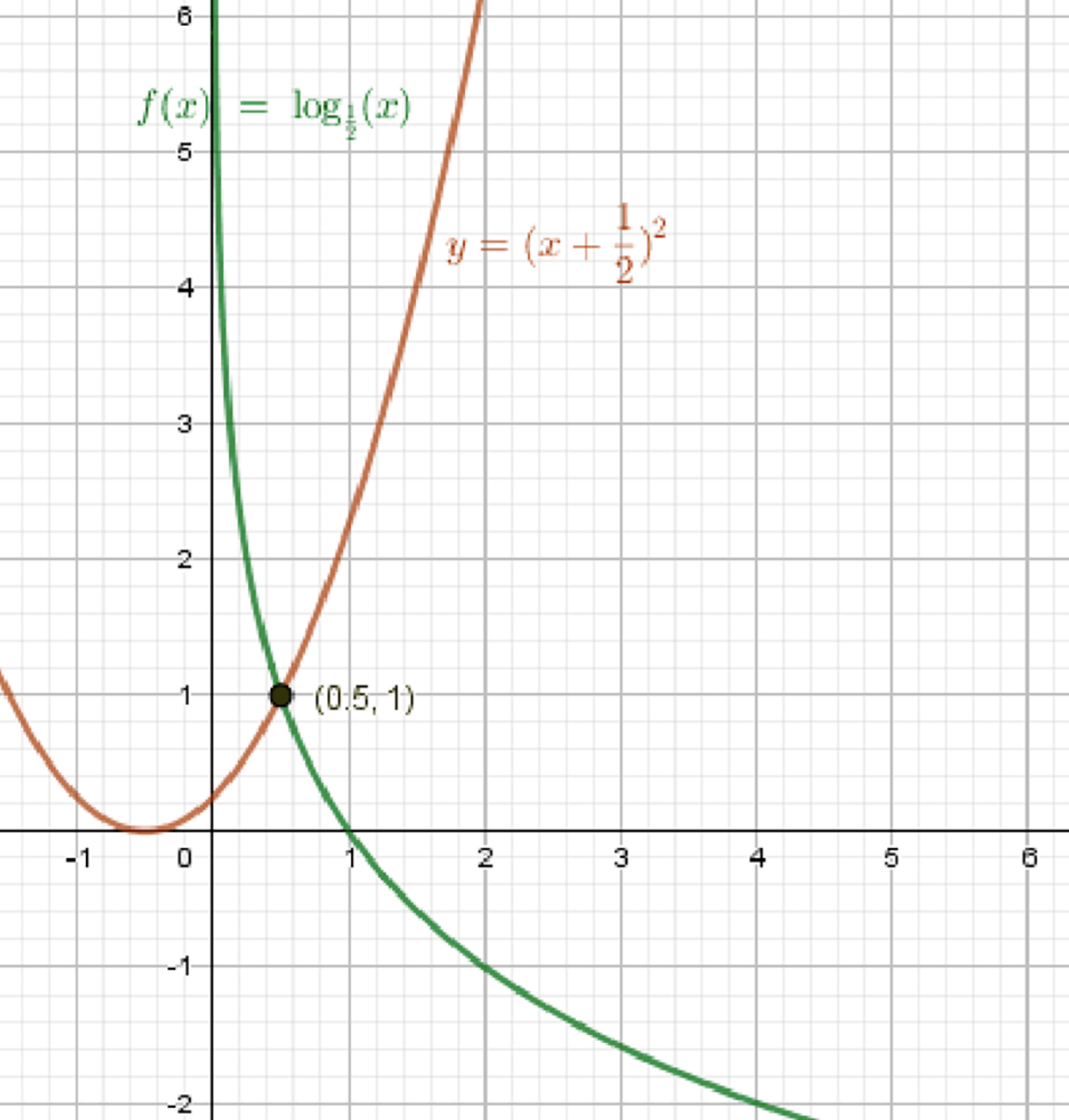
\( y = \log_{\frac{1}{2}} x \) — уравнение логарифмической функции:
| \( x \) | 0,5 | 1 | 2 |
|---|---|---|---|
| \( y \) | 1 | 0 | -1 |
\( y = \left( x + \frac{1}{2} \right)^2 \) — уравнение параболы:
\( x_0 = -0{,}5 \), \( y_0 = 0 \)
| \( x \) | 0,5 | 1,5 | 2,5 |
|---|---|---|---|
| \( y \) | 1 | 4 | 9 |
Графики функций:
Ответ: \( x = 0{,}5 \)
а) \( (x — 1)^2 = \log_2 x \)
Разделим уравнение на две функции:
- Функция \( y = (x — 1)^2 \) — парабола, с вершиной в точке \( (1, 0) \). Ветви направлены вверх.
- Функция \( y = \log_2 x \) — логарифмическая, определена при \( x > 0 \), проходит через точку \( (1, 0) \), возрастает.
Построим таблицу значений для функции \( y = (x — 1)^2 \):
| \( x \) | 2 | 3 | 4 |
|---|---|---|---|
| \( y \) | 1 | 4 | 9 |
Построим таблицу значений для функции \( y = \log_2 x \):
| \( x \) | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| \( y \) | 0 | 1 | 2 | 3 |
Обе функции проходят через точку \( (1, 0) \), значит:
- Первое решение уравнения: \( x = 1 \)
Подставим \( x = 2 \):
- \( (2 — 1)^2 = 1 \)
- \( \log_2 2 = 1 \)
Значения совпали ⇒
- Второе решение уравнения: \( x = 2 \)
Так как парабола возрастает при \( x > 1 \), а логарифмическая функция тоже возрастает, графики могут пересекаться максимум в одной точке на этом интервале. Аналогично — только одна точка пересечения на отрезке \( x < 1 \). Таким образом, других решений нет.
Ответ: \( x_1 = 1 \); \( x_2 = 2 \)
б) \( \log_{\frac{1}{2}} x = \left( x + \frac{1}{2} \right)^2 \)
Разделим уравнение на две функции:
- Функция \( y = \log_{\frac{1}{2}} x \) — убывающая логарифмическая функция, определена при \( x > 0 \).
- Функция \( y = \left( x + \frac{1}{2} \right)^2 \) — парабола с вершиной в точке \( (-\frac{1}{2}, 0) \), ветви направлены вверх.
Построим таблицу значений для \( y = \log_{\frac{1}{2}} x \):
| \( x \) | 0,5 | 1 | 2 |
|---|---|---|---|
| \( y \) | 1 | 0 | -1 |
Построим таблицу значений для \( y = \left( x + \frac{1}{2} \right)^2 \):
| \( x \) | 0,5 | 1,5 | 2,5 |
|---|---|---|---|
| \( y \) | 1 | 4 | 9 |
Обе функции проходят через точку \( (0{,}5, 1) \), следовательно:
- Это и есть единственное решение уравнения.
Поскольку логарифмическая функция убывает, а парабола возрастает при \( x > -\frac{1}{2} \), пересечение возможно только в одной точке.
Ответ: \( x = 0{,}5 \)