Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 57.24 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( \log_2 x < 6 — x \)
б) \( \log_3 x \geq x^3 \)
в) \( \log_2 x \geq 6 — x \)
г) \( \log_3 x < x^3 \)
Решить неравенство, применяя функционально-графические методы
а) \( \log_2 x < 6 — x \)
Выражение имеет смысл при:
\( x > 0 \).
Разделим неравенство на две функции:
- \( y = \log_2 x \) — возрастает при \( x > 0 \);
- \( g = 6 — x \) — убывает при \( x > 0 \).
Методом перебора найдем точку пересечения:
- \( y(4) = \log_2 4 = \log_2 2^2 = 2 \);
- \( g(4) = 6 — 4 = 2 \).
Ответ: \( x \in (0; 4) \).
б) \( \log_3 x \geq x^3 \)
\( y = \log_3 x \) — уравнение экспоненты:
| \( x \) | 1 | 3 | 9 |
|---|---|---|---|
| \( y \) | 0 | 1 | 2 |
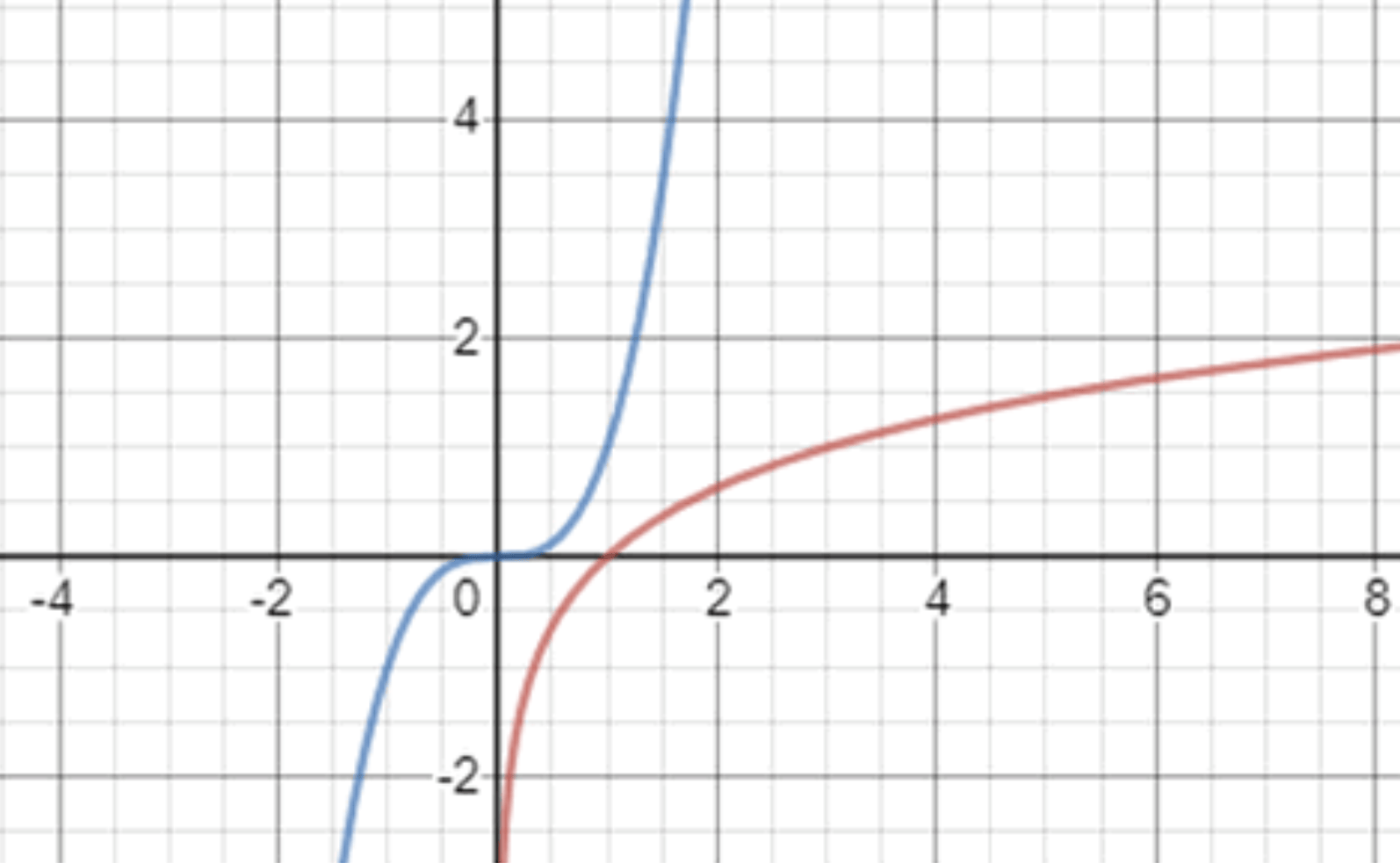
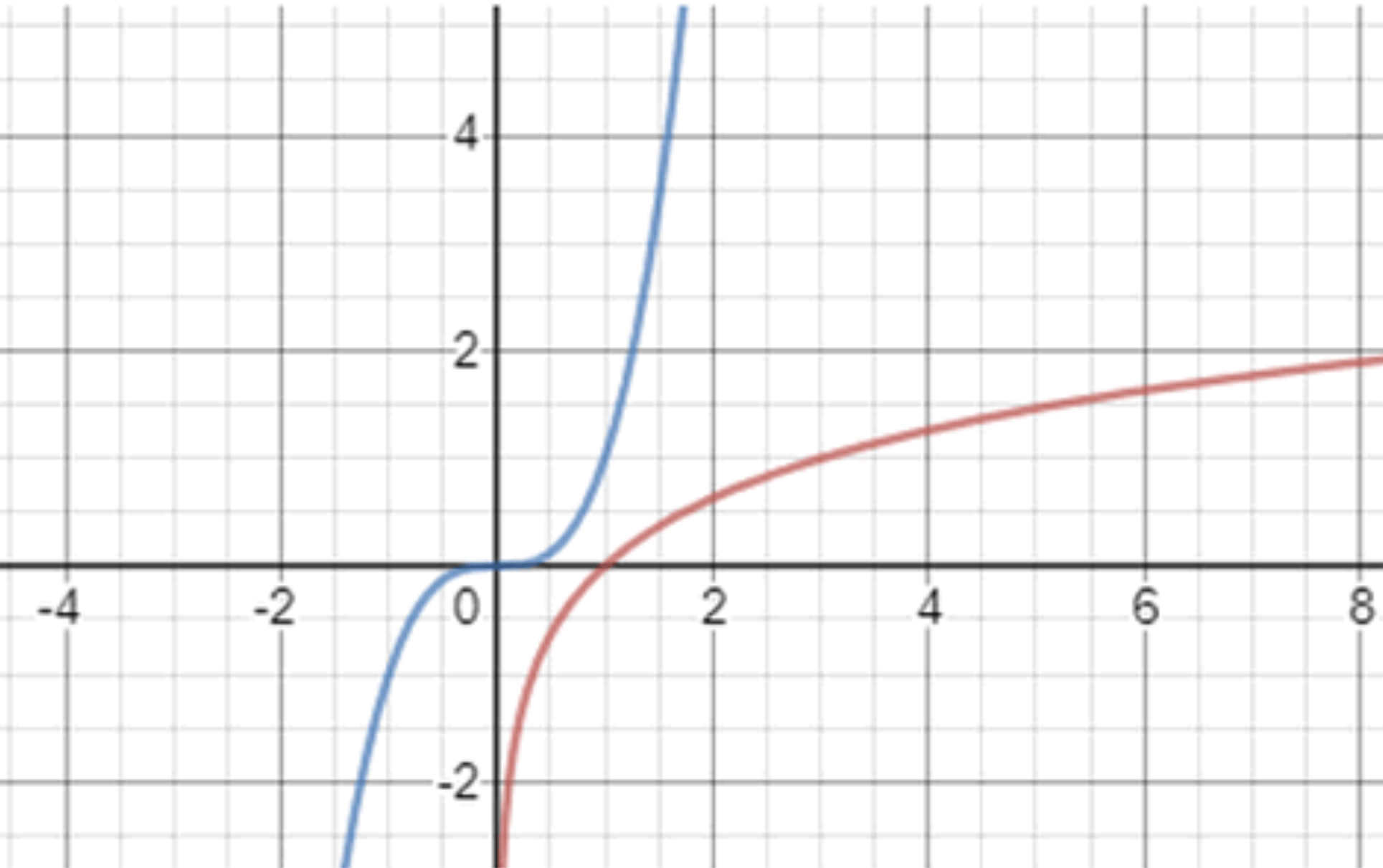
\( y = x^3 \) — кубическая парабола:
| \( x \) | 1 | 2 |
|---|---|---|
| \( y \) | 1 | 8 |
Выражение имеет смысл при:
\( x > 0 \).
Графики функций:
Ответ: \( x \in ø \).
в) \( \log_2 x \geq 6 — x \)
Выражение имеет смысл при:
\( x > 0 \).
Разделим неравенство на две функции:
- \( y = \log_2 x \) — возрастает при \( x > 0 \);
- \( g = 6 — x \) — убывает при \( x > 0 \).
Методом перебора найдем точку пересечения:
- \( y(4) = \log_2 4 = \log_2 2^2 = 2 \);
- \( g(4) = 6 — 4 = 2 \).
Ответ: \( x \in [4; +\infty) \).
г) \( \log_3 x < x^3 \)
\( y = \log_3 x \) — уравнение экспоненты:
| \( x \) | 1 | 3 | 9 |
|---|---|---|---|
| \( y \) | 0 | 1 | 2 |
\( y = x^3 \) — кубическая парабола:
| \( x \) | 1 | 2 |
|---|---|---|
| \( y \) | 1 | 8 |
Выражение имеет смысл при:
\( x > 0 \).
Графики функций:
Ответ: \( x \in (0; +\infty) \).
а) \( \log_2 x < 6 — x \)
Шаг 1: Определим область допустимых значений (ОДЗ).
Выражение имеет смысл при:
\( x > 0 \), так как логарифмическая функция определена только при положительных значениях \( x \).
Шаг 2: Разделим неравенство на две функции:
- \( y = \log_2 x \) — логарифмическая функция, которая возрастает при \( x > 0 \);
- \( g = 6 — x \) — линейная функция, которая убывает при \( x > 0 \).
Шаг 3: Найдем точку пересечения графиков методом подстановки.
- Подставим \( x = 4 \):
- \( y(4) = \log_2 4 = \log_2 2^2 = 2 \);
- \( g(4) = 6 — 4 = 2 \).
Точка пересечения графиков — \( x = 4 \).
Шаг 4: Анализ поведения функций.
Функция \( y = \log_2 x \) возрастает, а функция \( g = 6 — x \) убывает. Неравенство \( \log_2 x < 6 — x \) выполняется для всех \( x \in (0; 4) \).
Ответ: \( x \in (0; 4) \).
б) \( \log_3 x \geq x^3 \)
Шаг 1: Определим область допустимых значений (ОДЗ).
Выражение имеет смысл при:
\( x > 0 \), так как логарифмическая функция и кубическая функция определены при положительных значениях \( x \).
Шаг 2: Разделим неравенство на две функции:
- \( y = \log_3 x \) — логарифмическая функция, которая возрастает при \( x > 0 \);
- \( y = x^3 \) — кубическая парабола, которая возрастает при \( x > 0 \).
Шаг 3: Построим таблицу значений для обеих функций.
Для функции \( y = \log_3 x \):
| \( x \) | 1 | 3 | 9 |
|---|---|---|---|
| \( y \) | 0 | 1 | 2 |
Для функции \( y = x^3 \):
| \( x \) | 1 | 2 |
|---|---|---|
| \( y \) | 1 | 8 |
Шаг 4: Анализ поведения функций.
Функция \( y = x^3 \) возрастает быстрее, чем функция \( y = \log_3 x \). Графики не пересекаются.
Следовательно, неравенство \( \log_3 x \geq x^3 \) не имеет решений.
Ответ: \( x \in ø \).
в) \( \log_2 x \geq 6 — x \)
Шаг 1: Определим область допустимых значений (ОДЗ).
Выражение имеет смысл при:
\( x > 0 \), так как логарифмическая функция определена только при положительных значениях \( x \).
Шаг 2: Разделим неравенство на две функции:
- \( y = \log_2 x \) — логарифмическая функция, которая возрастает при \( x > 0 \);
- \( g = 6 — x \) — линейная функция, которая убывает при \( x > 0 \).
Шаг 3: Найдем точку пересечения графиков методом подстановки.
- Подставим \( x = 4 \):
- \( y(4) = \log_2 4 = \log_2 2^2 = 2 \);
- \( g(4) = 6 — 4 = 2 \).
Точка пересечения графиков — \( x = 4 \).
Шаг 4: Анализ поведения функций.
Функция \( y = \log_2 x \) возрастает, а функция \( g = 6 — x \) убывает. Неравенство \( \log_2 x \geq 6 — x \) выполняется для всех \( x \in [4; +\infty) \).
Ответ: \( x \in [4; +\infty) \).
г) \( \log_3 x < x^3 \)
Шаг 1: Определим область допустимых значений (ОДЗ).
Выражение имеет смысл при:
\( x > 0 \), так как логарифмическая функция и кубическая функция определены при положительных значениях \( x \).
Шаг 2: Разделим неравенство на две функции:
- \( y = \log_3 x \) — логарифмическая функция, которая возрастает при \( x > 0 \);
- \( y = x^3 \) — кубическая парабола, которая возрастает при \( x > 0 \).
Шаг 3: Построим таблицу значений для обеих функций.
Для функции \( y = \log_3 x \):
| \( x \) | 1 | 3 | 9 |
|---|---|---|---|
| \( y \) | 0 | 1 | 2 |
Для функции \( y = x^3 \):
| \( x \) | 1 | 2 |
|---|---|---|
| \( y \) | 1 | 8 |
Шаг 4: Анализ поведения функций.
Функция \( y = x^3 \) возрастает быстрее, чем функция \( y = \log_3 x \). Неравенство \( \log_3 x < x^3 \) выполняется для всех \( x \in (0; +\infty) \).
Ответ: \( x \in (0; +\infty) \).