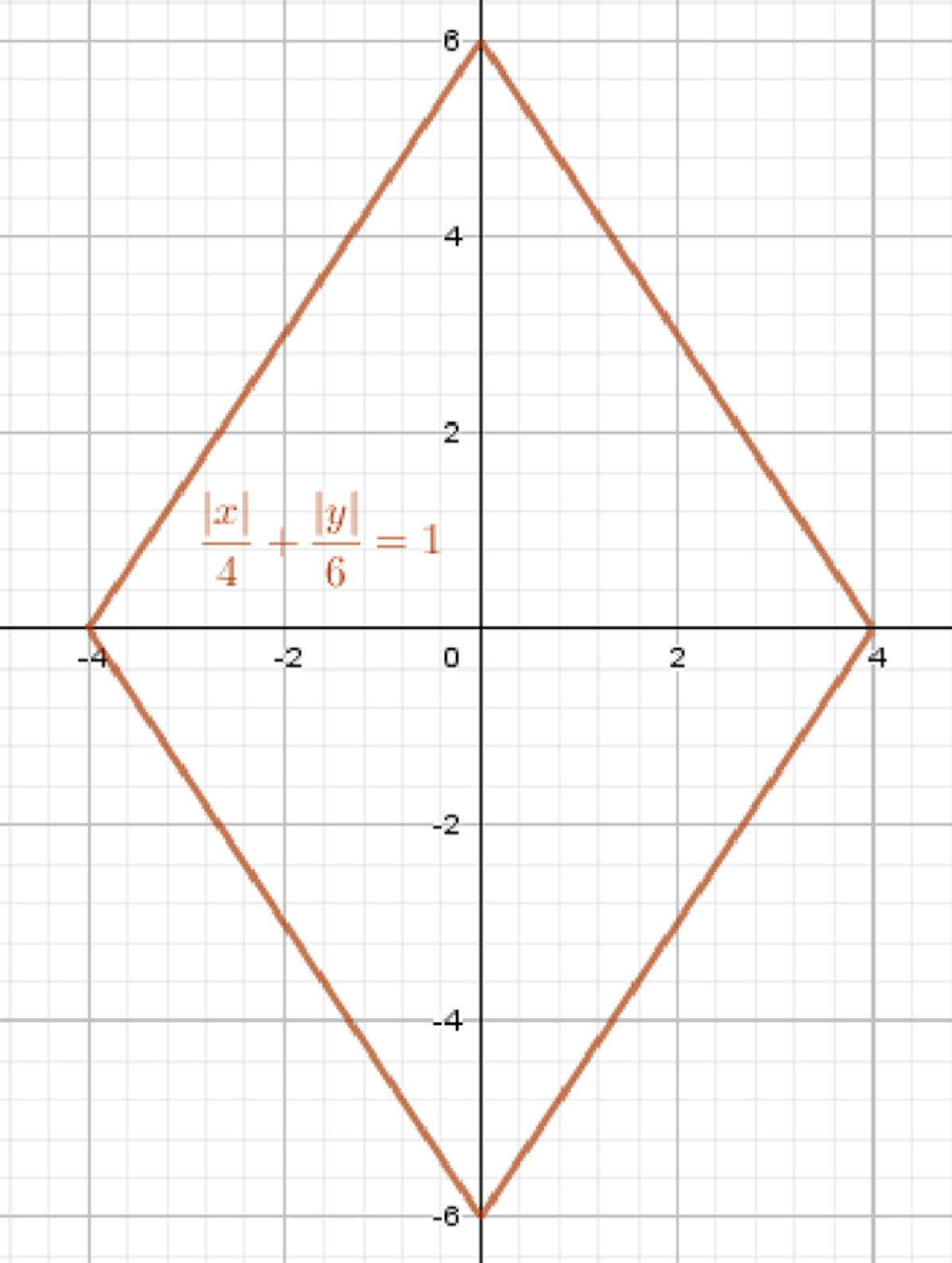Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.10 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте график уравнения и вычислите площадь фигуры, которая ограничена этим графиком:
а) \( 2|x| + 3|y| = 6 \)
б) \( 0.5|x| + \frac{1}{3}|y| = 2 \)
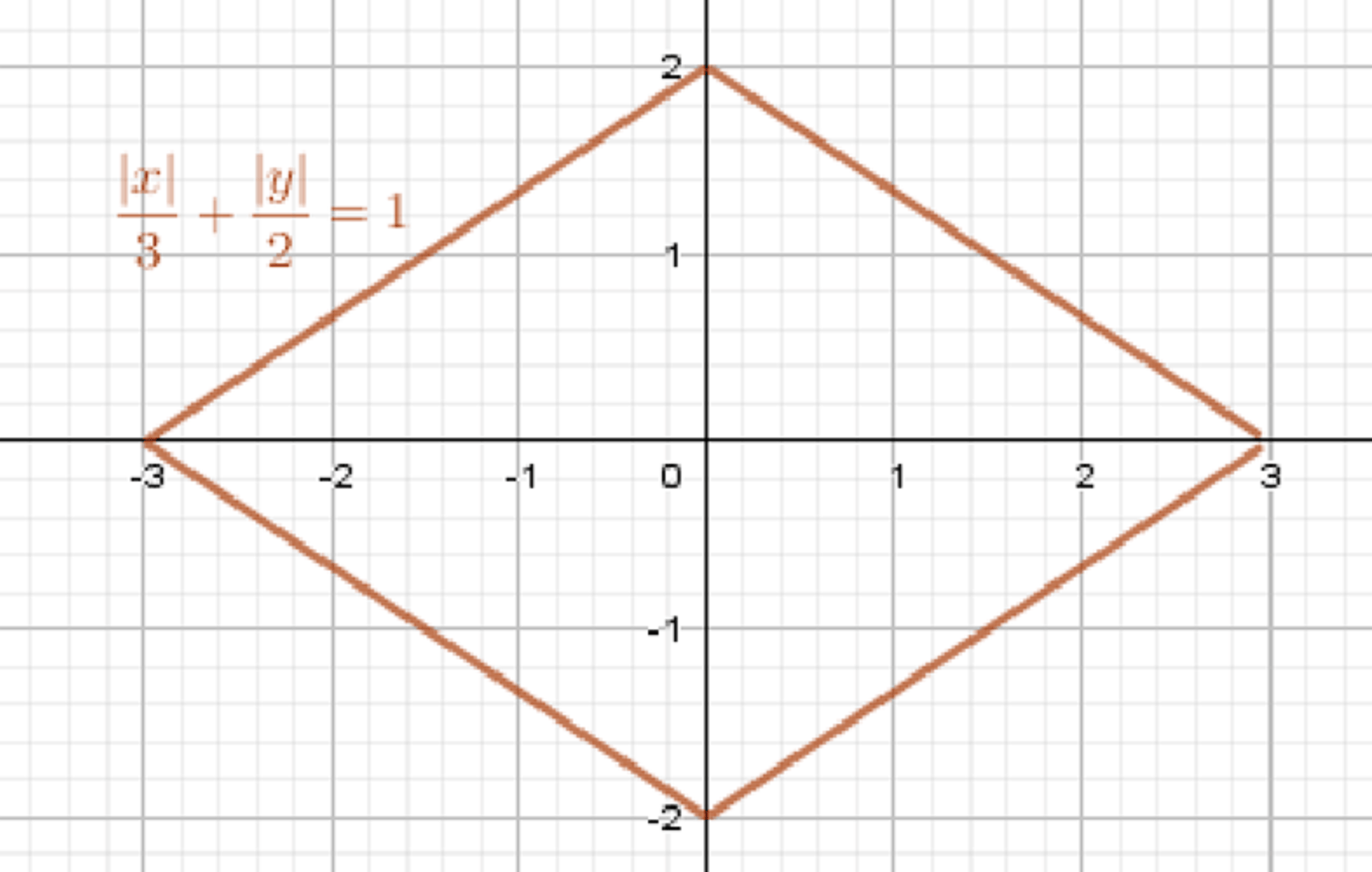
а) \( 2|x| + 3|y| = 6 \)
Если \( x \geq 0 \) и \( y \geq 0 \), тогда:
\(2x + 3y = 6;\)
\(3y = -2x + 6;\)
\(y = -\frac{2}{3}x + 2;\)
Таблица значений:
\[
\begin{array}{|c|c|}
\hline
x & y \\
\hline
0 & 2 \\
\hline
3 & 0 \\
\hline
\end{array}
\]
График симметричен относительно осей координат.
Площадь фигуры:
\[
S = 4 \cdot \left( \frac{1}{2} \cdot 3 \cdot 2 \right) = 4 \cdot 3 = 12;
\]
Ответ: 12.
б) \( 0.5|x| + \frac{1}{3}|y| = 2 \)
Если \( x \geq 0 \) и \( y \geq 0 \), тогда:
\(0.5x + \frac{1}{3}y = 2 \quad \big| \cdot 6;\)
\(3x + 2y = 12;\)
\(2y = -3x + 12;\)
\(y = -\frac{3}{2}x + 6;\)
Таблица значений:
\[
\begin{array}{|c|c|}
\hline
x & y \\
\hline
0 & 6 \\
\hline
4 & 0 \\
\hline
\end{array}
\]
График симметричен относительно осей координат.
Площадь фигуры:
\[
S = 4 \cdot \left( \frac{1}{2} \cdot 4 \cdot 6 \right) = 4 \cdot 12 = 48;
\]
Ответ: 48.
а) \( 2|x| + 3|y| = 6 \)
Рассмотрим случай, когда \( x \geq 0 \) и \( y \geq 0 \). Тогда модуль можно убрать, и уравнение принимает вид:
\[
2x + 3y = 6.
\]
Выразим \( y \) через \( x \):
\[
3y = -2x + 6.
\]
Разделим обе части на 3:
\[
y = -\frac{2}{3}x + 2.
\]
Теперь составим таблицу значений для удобства построения графика:
\[
\begin{array}{|c|c|}
\hline
x & y \\
\hline
0 & 2 \\
\hline
3 & 0 \\
\hline
\end{array}
\]
График прямой линии симметричен относительно осей координат, так как в уравнении присутствуют модули \( |x| \) и \( |y| \). Это означает, что достаточно построить график для первой четверти, а затем отразить его относительно осей \( x \) и \( y \).
Построенная фигура представляет собой ромб. Найдем его площадь.
Площадь одной из четырех частей фигуры (треугольника) равна:
\[
S_{\text{треугольник}} = \frac{1}{2} \cdot \text{основание} \cdot \text{высота} = \frac{1}{2} \cdot 3 \cdot 2 = 3.
\]
Так как ромб состоит из четырех таких треугольников, его площадь равна:
\[
S = 4 \cdot S_{\text{треугольник}} = 4 \cdot 3 = 12.
\]
Ответ: 12.
б) \( 0.5|x| + \frac{1}{3}|y| = 2 \)
Рассмотрим случай, когда \( x \geq 0 \) и \( y \geq 0 \). Тогда модуль можно убрать, и уравнение принимает вид:
\[
0.5x + \frac{1}{3}y = 2.
\]
Для удобства умножим обе части уравнения на 6, чтобы избавиться от дробей:
\[
6 \cdot \left( 0.5x + \frac{1}{3}y \right) = 6 \cdot 2.
\]
Раскроем скобки:
\[
3x + 2y = 12.
\]
Выразим \( y \) через \( x \):
\[
2y = -3x + 12.
\]
Разделим обе части на 2:
\[
y = -\frac{3}{2}x + 6.
\]
Теперь составим таблицу значений для удобства построения графика:
\[
\begin{array}{|c|c|}
\hline
x & y \\
\hline
0 & 6 \\
\hline
4 & 0 \\
\hline
\end{array}
\]
График прямой линии симметричен относительно осей координат, так как в уравнении присутствуют модули \( |x| \) и \( |y| \). Это означает, что достаточно построить график для первой четверти, а затем отразить его относительно осей \( x \) и \( y \).
Построенная фигура представляет собой ромб. Найдем его площадь.
Площадь одной из четырех частей фигуры (треугольника) равна:
\[
S_{\text{треугольник}} = \frac{1}{2} \cdot \text{основание} \cdot \text{высота} = \frac{1}{2} \cdot 4 \cdot 6 = 12.
\]
Так как ромб состоит из четырех таких треугольников, его площадь равна:
\[
S = 4 \cdot S_{\text{треугольник}} = 4 \cdot 12 = 48.
\]
Ответ: 48.