Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.15 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
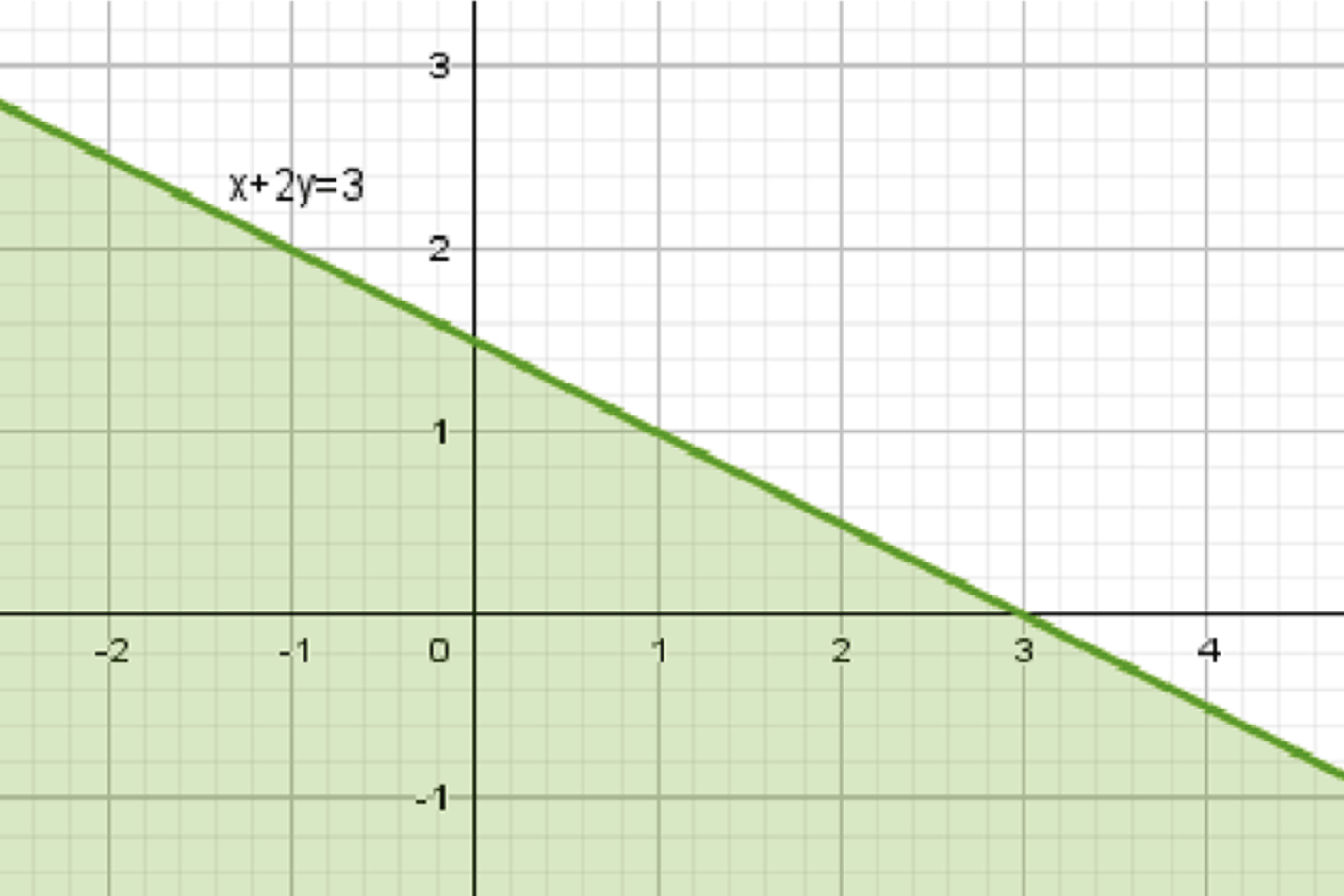
а) \(x + 2y \leq 3\);
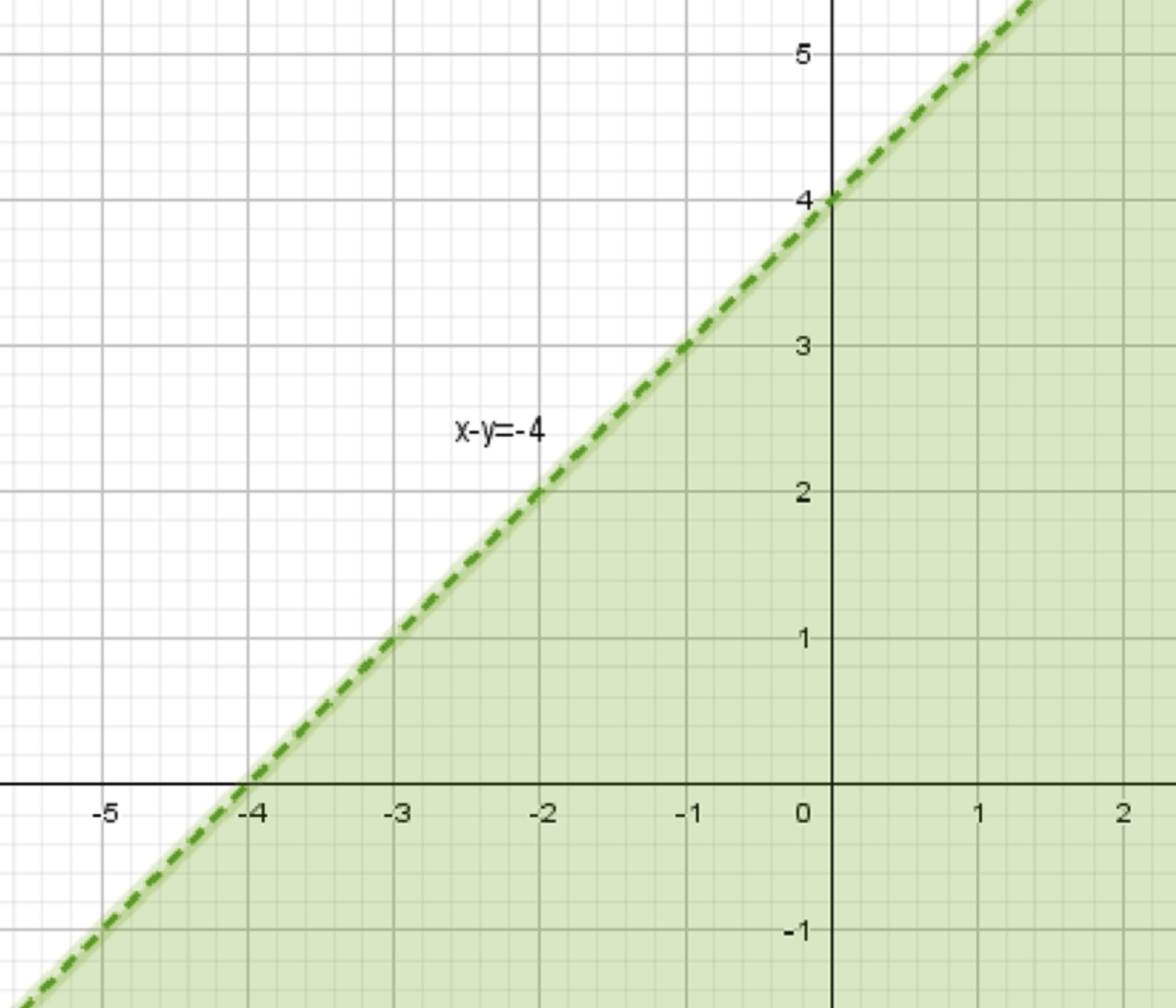
б) \(x — y > -4\);
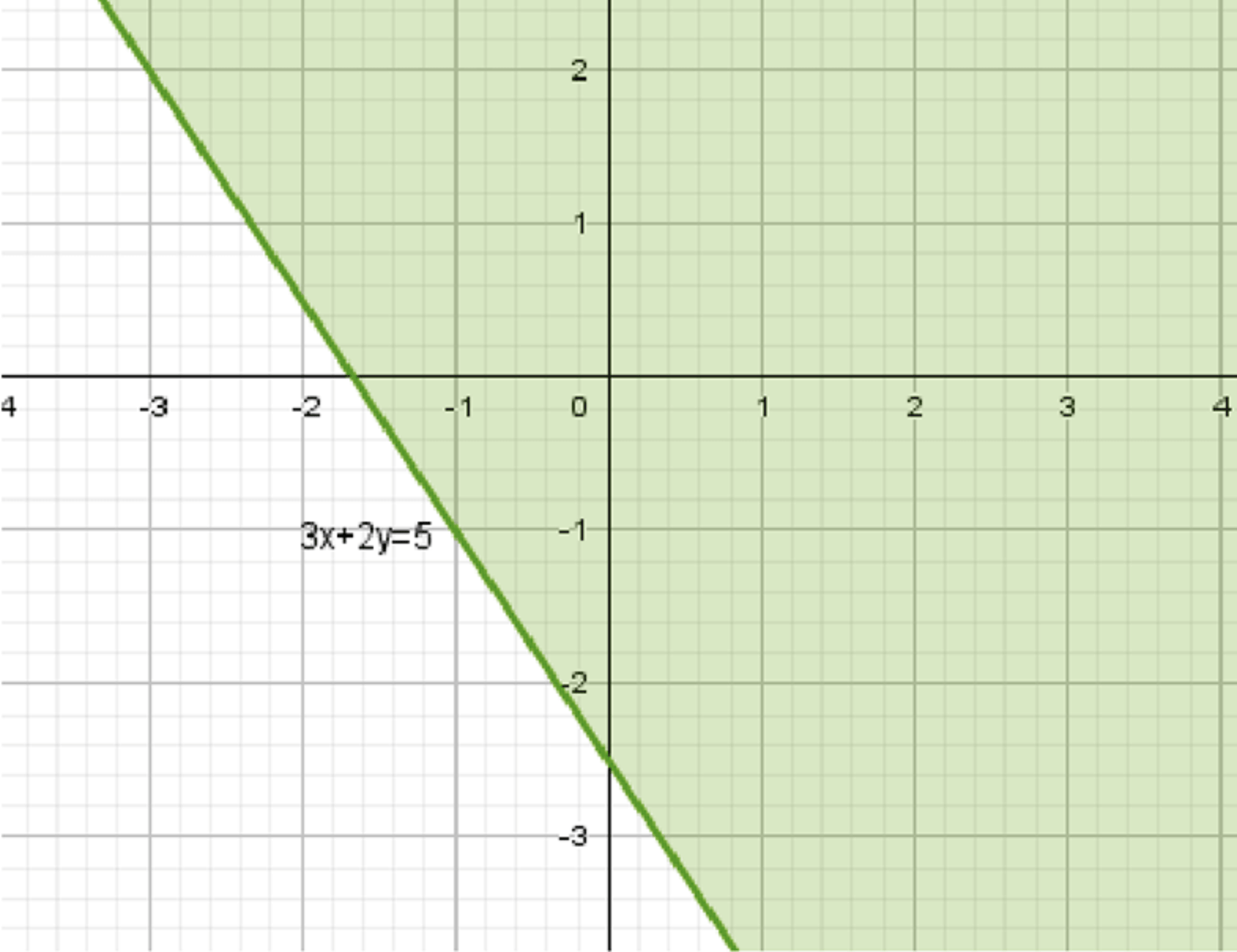
в) \(3x + 2y \geq -5\);
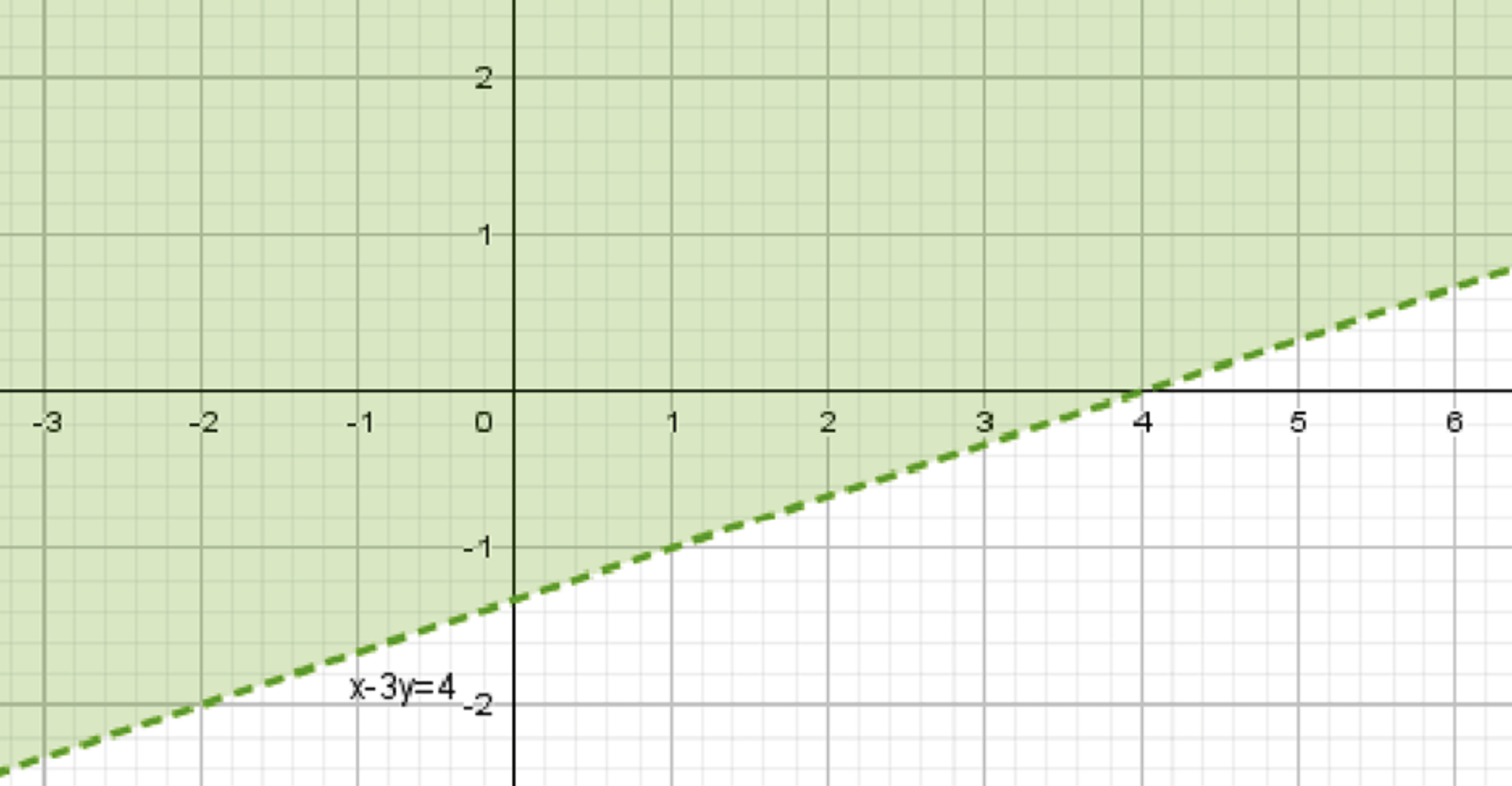
г) \(x — 3y < 4\)
Построить множество точек координатной плоскости, удовлетворяющих неравенству:
а) \(x + 2y \leq 3\);
\(2y \leq -x + 3\);
\(y \leq -\frac{1}{2}x + \frac{3}{2}\);
Дано уравнение прямой:
| \(x\) | -1 | 3 |
|---|---|---|
| \(y\) | 2 | 0 |
Множество точек:
б) \(x — y > -4\);
\(y < x + 4\);
Дано уравнение прямой:
| \(x\) | -4 | 0 |
|---|---|---|
| \(y\) | 0 | 4 |
Множество точек:
в) \(3x + 2y \geq -5\);
\(2y \geq -3x — 5\);
\(y \geq -\frac{3}{2}x — \frac{5}{2}\);
Дано уравнение прямой:
| \(x\) | -1 | 1 |
|---|---|---|
| \(y\) | -1 | -4 |
Множество точек:
г) \(x — 3y < 4\);
\(3y > x — 4\);
\(y > \frac{1}{3}x — \frac{4}{3}\);
Дано уравнение прямой:
| \(x\) | -2 | 4 |
|---|---|---|
| \(y\) | -2 | 0 |
Множество точек:
а) \(x + 2y \leq 3\);
Преобразуем неравенство к виду \(y \leq kx + b\):
\(x + 2y \leq 3\);
\(2y \leq -x + 3\);
\(y \leq -\frac{1}{2}x + \frac{3}{2}\).
Уравнение прямой, соответствующей границе области:
\(y = -\frac{1}{2}x + \frac{3}{2}\).
Найдем точки для построения графика:
| \(x\) | -1 | 3 |
|---|---|---|
| \(y\) | 2 | 0 |
Подставляем значения \(x\) в уравнение \(y = -\frac{1}{2}x + \frac{3}{2}\):
1. При \(x = -1\):
\(y = -\frac{1}{2}(-1) + \frac{3}{2} = \frac{1}{2} + \frac{3}{2} = 2\);
2. При \(x = 3\):
\(y = -\frac{1}{2}(3) + \frac{3}{2} = -\frac{3}{2} + \frac{3}{2} = 0\).
Таким образом, точки прямой: \((-1; 2)\) и \((3; 0)\).
График прямой делит плоскость на две области. Так как неравенство \(y \leq -\frac{1}{2}x + \frac{3}{2}\), то искомая область находится ниже прямой.
Множество точек: все точки, лежащие ниже прямой \(y = -\frac{1}{2}x + \frac{3}{2}\), включая саму прямую.
б) \(x — y > -4\);
Преобразуем первое неравенство:
\(x — y > -4\);
\(-y > -x — 4\);
\(y < x + 4\).
Уравнение прямой, соответствующей границе области:
\(y = x + 4\).
Найдем точки для построения графика:
| \(x\) | -4 | 0 |
|---|---|---|
| \(y\) | 0 | 4 |
Подставляем значения \(x\) в уравнение \(y = x + 4\):
1. При \(x = -4\):
\(y = -4 + 4 = 0\);
2. При \(x = 0\):
\(y = 0 + 4 = 4\).
Таким образом, точки прямой: \((-4; 0)\) и \((0; 4)\).
График прямой делит плоскость на две области. Так как неравенство \(y < x + 4\), то искомая область находится ниже прямой.
Множество точек: все точки, лежащие ниже прямой \(y = x + 4\).
в) \(3x + 2y \geq -5\);
Преобразуем неравенство к виду \(y \geq kx + b\):
\(3x + 2y \geq -5\);
\(2y \geq -3x — 5\);
\(y \geq -\frac{3}{2}x — \frac{5}{2}\).
Уравнение прямой, соответствующей границе области:
\(y = -\frac{3}{2}x — \frac{5}{2}\).
Найдем точки для построения графика:
| \(x\) | -1 | 1 |
|---|---|---|
| \(y\) | -1 | -4 |
Подставляем значения \(x\) в уравнение \(y = -\frac{3}{2}x — \frac{5}{2}\):
1. При \(x = -1\):
\(y = -\frac{3}{2}(-1) — \frac{5}{2} = \frac{3}{2} — \frac{5}{2} = -1\);
2. При \(x = 1\):
\(y = -\frac{3}{2}(1) — \frac{5}{2} = -\frac{3}{2} — \frac{5}{2} = -4\).
Таким образом, точки прямой: \((-1; -1)\) и \((1; -4)\).
График прямой делит плоскость на две области. Так как неравенство \(y \geq -\frac{3}{2}x — \frac{5}{2}\), то искомая область находится выше прямой.
Множество точек: все точки, лежащие выше прямой \(y = -\frac{3}{2}x — \frac{5}{2}\), включая саму прямую.
г) \(x — 3y < 4\);
Преобразуем неравенство к виду \(y > kx + b\):
\(x — 3y < 4\);
\(-3y < -x + 4\);
\(y > \frac{1}{3}x — \frac{4}{3}\).
Уравнение прямой, соответствующей границе области:
\(y = \frac{1}{3}x — \frac{4}{3}\).
Найдем точки для построения графика:
| \(x\) | -2 | 4 |
|---|---|---|
| \(y\) | -2 | 0 |
Подставляем значения \(x\) в уравнение \(y = \frac{1}{3}x — \frac{4}{3}\):
1. При \(x = -2\):
\(y = \frac{1}{3}(-2) — \frac{4}{3} = -\frac{2}{3} — \frac{4}{3} = -2\);
2. При \(x = 4\):
\(y = \frac{1}{3}(4) — \frac{4}{3} = \frac{4}{3} — \frac{4}{3} = 0\).
Таким образом, точки прямой: \((-2; -2)\) и \((4; 0)\).
График прямой делит плоскость на две области. Так как неравенство \(y > \frac{1}{3}x — \frac{4}{3}\), то искомая область находится выше прямой.
Множество точек: все точки, лежащие выше прямой \(y = \frac{1}{3}x — \frac{4}{3}\).