Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.16 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств:
а) \( \begin{cases}
x + y \geq 3 \\
2x — 3y \leq 1
\end{cases} \)
б) \( \begin{cases}
x — y \geq 1 \\
x + y \leq 1 \\
x \leq 2y
\end{cases} \)
в) \( \begin{cases}
x — 2y \geq 3 \\
x + 3y \leq -2
\end{cases} \)
г) \( \begin{cases}
x — y \geq 2x \\
x + y \leq 3y \\
5x \leq 2y — 7
\end{cases} \)
Построить на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств:
а) \( \begin{cases}
x + y \geq 3 \\
2x — 3y \leq 1
\end{cases} \)
Первое неравенство:
\( x + y \geq 3; \)
\( y \geq 3 — x; \)
\( \begin{array}{c|c|c}
x & 0 & 3 \\
\hline
y & 3 & 0
\end{array} \)
Второе неравенство:
\( 2x — 3y \leq 1; \)
\( 3y \geq 2x — 1; \)
\( y \geq \frac{2}{3}x — \frac{1}{3}; \)
\( \begin{array}{c|c|c}
x & -1 & 2 \\
\hline
y & -1 & 1
\end{array} \)
Множество точек:
б) \( \begin{cases}
x — y \geq 1 \\
x + y \leq 1 \\
x \leq 2y
\end{cases} \)
Первое неравенство:
\( x — y \geq 1; \)
\( y \leq x — 1; \)
\( \begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & -1 & 1
\end{array} \)
Второе неравенство:
\( x + y \leq 1; \)
\( y \leq 1 — x; \)
\( \begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & 1 & -1
\end{array} \)
Третье неравенство:
\( x \leq 2y; \)
\( y \geq \frac{1}{2}x; \)
\( \begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & 0 & 1
\end{array} \)
Множество точек:
(Нет решений);
в) \( \begin{cases}
x — 2y \geq 3 \\
x + 3y \leq -2
\end{cases} \)
Первое неравенство:
\( x — 2y \geq 3; \)
\( 2y \leq x — 3; \)
\( y \leq \frac{1}{2}x — \frac{3}{2}; \)
\( \begin{array}{c|c|c}
x & 1 & 3 \\
\hline
y & -1 & 0
\end{array} \)
Второе неравенство:
\( x + 3y \leq -2; \)
\( 3y \leq -x — 2; \)
\( y \leq -\frac{1}{3}x — \frac{2}{3}; \)
\( \begin{array}{c|c|c}
x & -2 & 4 \\
\hline
y & 0 & -2
\end{array} \)
Множество точек:
г) \( \begin{cases}
x — y \geq 2x \\
x + y \leq 3y \\
5x \leq 2y — 7
\end{cases} \)
Первое неравенство:
\( x — y \geq 2x; \)
\( y \leq -x; \)
\( \begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & 0 & -2
\end{array} \)
Второе неравенство:
\( x + y \leq 3y; \)
\( 2y \geq x; \)
\( y \geq \frac{1}{2}x; \)
\( \begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & 0 & 1
\end{array} \)
Третье неравенство:
\( 5x \leq 2y — 7; \)
\( 2y \geq 5x + 7; \)
\( y \geq \frac{5}{2}x + \frac{7}{2}; \)
\( \begin{array}{c|c|c}
x & -3 & 1 \\
\hline
y & -4 & 6
\end{array} \)
Множество точек:
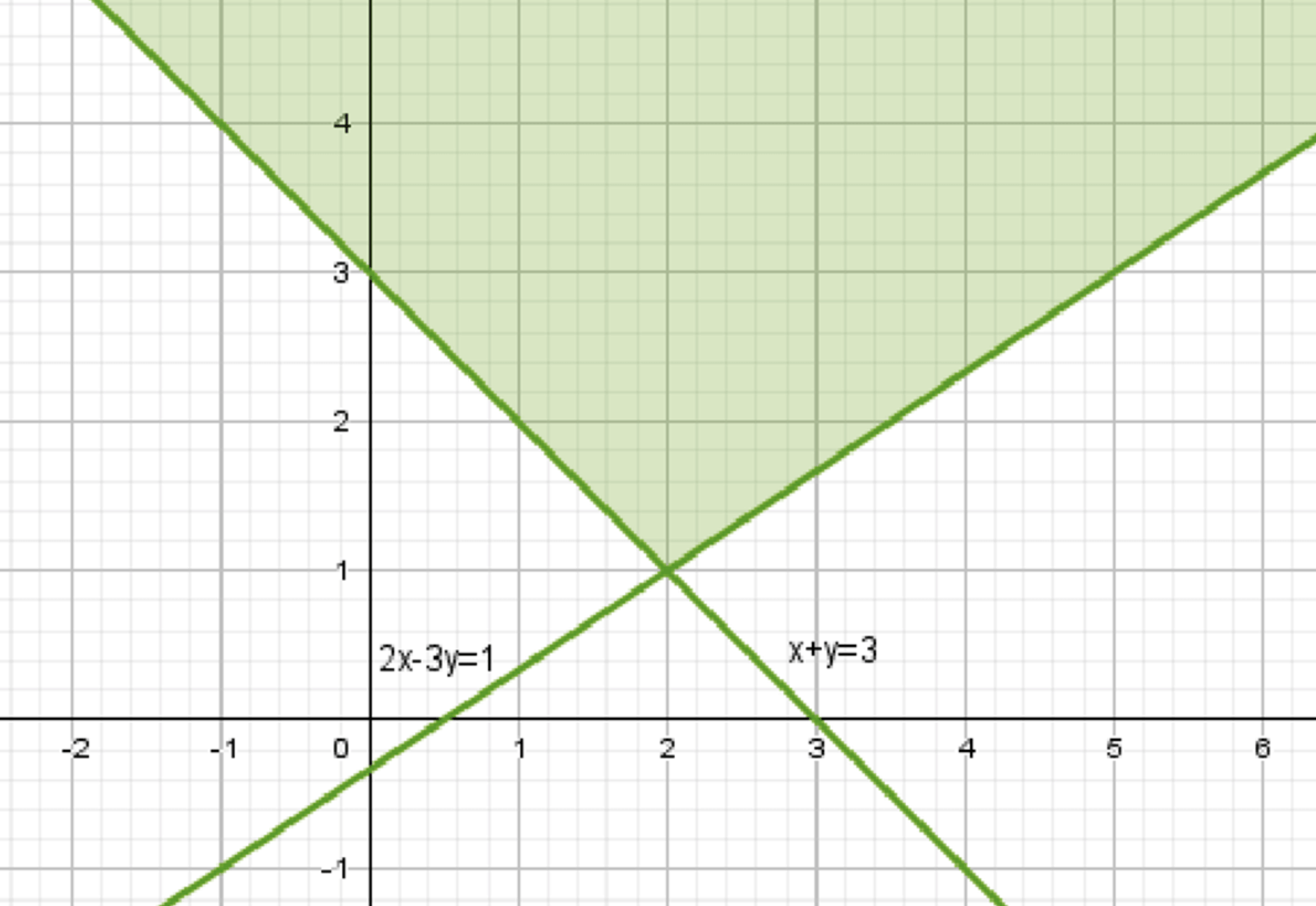
а) Дана система неравенств:
\( \begin{cases}
x + y \geq 3 \\
2x — 3y \leq 1
\end{cases} \)
Рассмотрим первое неравенство:
\( x + y \geq 3 \)
Выразим \( y \):
\( y \geq 3 — x \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & 0 & 3 \\
\hline
y & 3 & 0 \\
\end{array}
\]
График первого неравенства представляет собой прямую \( y = 3 — x \), выше которой лежат все точки, удовлетворяющие неравенству.
Рассмотрим второе неравенство:
\( 2x — 3y \leq 1 \)
Выразим \( y \):
\( 3y \geq 2x — 1 \)
\( y \geq \frac{2}{3}x — \frac{1}{3} \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & -1 & 2 \\
\hline
y & -1 & 1 \\
\end{array}
\]
График второго неравенства представляет собой прямую \( y = \frac{2}{3}x — \frac{1}{3} \), выше которой лежат все точки, удовлетворяющие неравенству.
Множество точек:
Множество точек, удовлетворяющих системе неравенств, находится в области пересечения двух полуплоскостей.
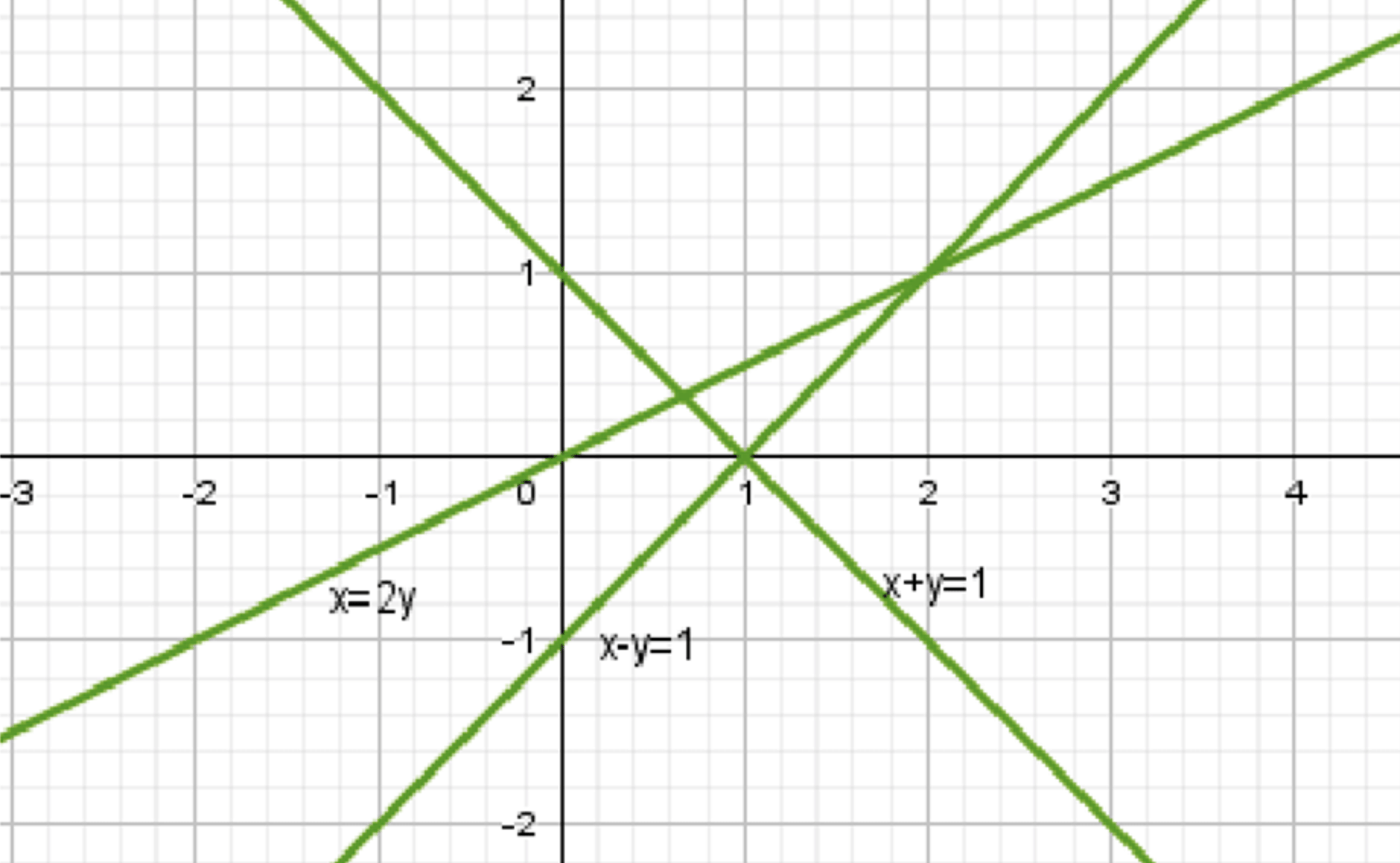
б) Дана система неравенств:
\( \begin{cases}
x — y \geq 1 \\
x + y \leq 1 \\
x \leq 2y
\end{cases} \)
Рассмотрим первое неравенство:
\( x — y \geq 1 \)
Выразим \( y \):
\( y \leq x — 1 \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & -1 & 1 \\
\end{array}
\]
График первого неравенства представляет собой прямую \( y = x — 1 \), ниже которой лежат все точки, удовлетворяющие неравенству.
Рассмотрим второе неравенство:
\( x + y \leq 1 \)
Выразим \( y \):
\( y \leq 1 — x \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & 1 & -1 \\
\end{array}
\]
График второго неравенства представляет собой прямую \( y = 1 — x \), ниже которой лежат все точки, удовлетворяющие неравенству.
Рассмотрим третье неравенство:
\( x \leq 2y \)
Выразим \( y \):
\( y \geq \frac{1}{2}x \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & 0 & 1 \\
\end{array}
\]
График третьего неравенства представляет собой прямую \( y = \frac{1}{2}x \), выше которой лежат все точки, удовлетворяющие неравенству.
Множество точек:
Область пересечения всех трех полуплоскостей пуста. Решений нет.
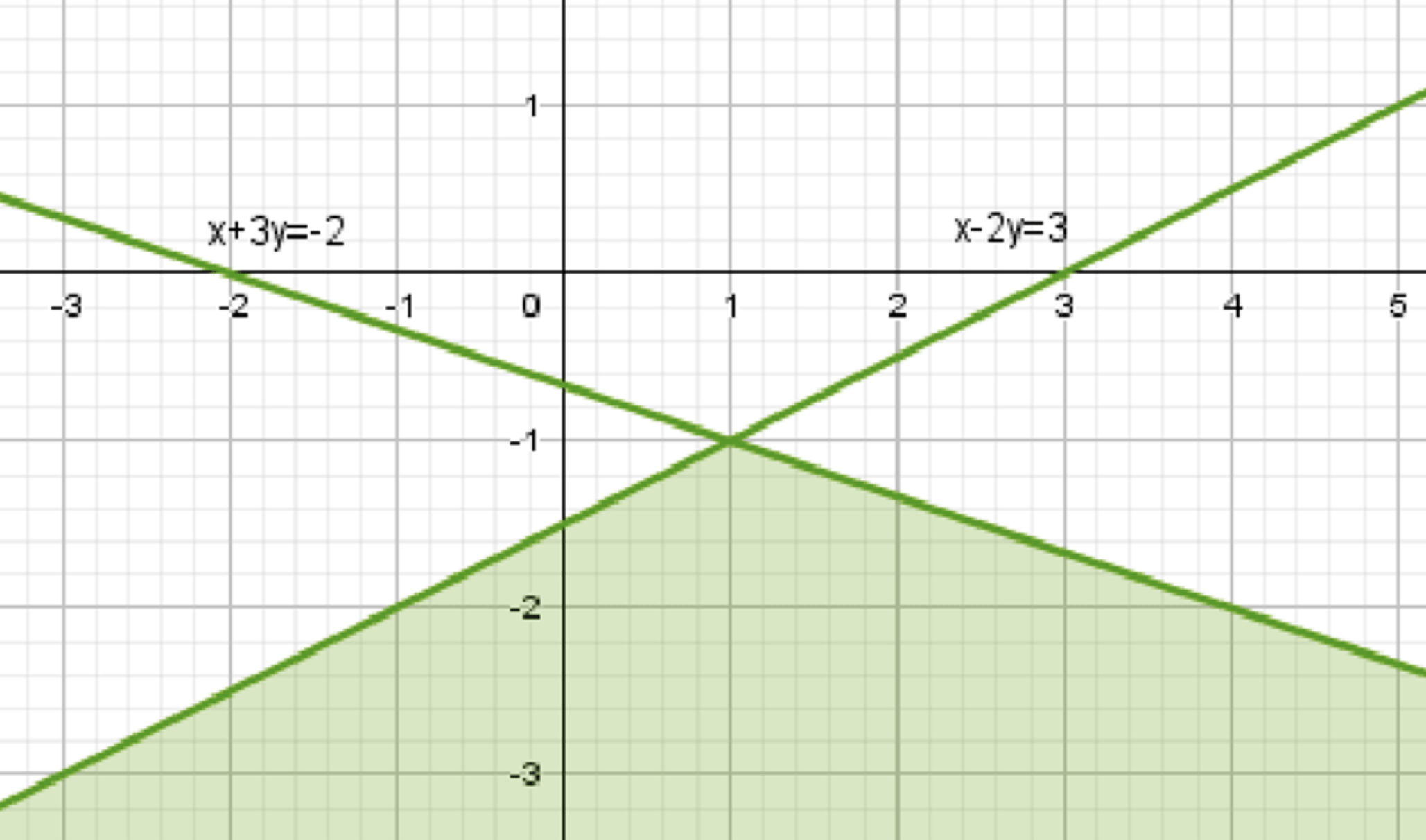
в) Дана система неравенств:
\( \begin{cases}
x — 2y \geq 3 \\
x + 3y \leq -2
\end{cases} \)
Рассмотрим первое неравенство:
\( x — 2y \geq 3 \)
Выразим \( y \):
\( 2y \leq x — 3 \)
\( y \leq \frac{1}{2}x — \frac{3}{2} \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & 1 & 3 \\
\hline
y & -1 & 0 \\
\end{array}
\]
График первого неравенства представляет собой прямую \( y = \frac{1}{2}x — \frac{3}{2} \), ниже которой лежат все точки, удовлетворяющие неравенству.
Рассмотрим второе неравенство:
\( x + 3y \leq -2 \)
Выразим \( y \):
\( 3y \leq -x — 2 \)
\( y \leq -\frac{1}{3}x — \frac{2}{3} \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & -2 & 4 \\
\hline
y & 0 & -2 \\
\end{array}
\]
График второго неравенства представляет собой прямую \( y = -\frac{1}{3}x — \frac{2}{3} \), ниже которой лежат все точки, удовлетворяющие неравенству.
Множество точек:
Множество точек, удовлетворяющих системе неравенств, находится в области пересечения двух полуплоскостей.
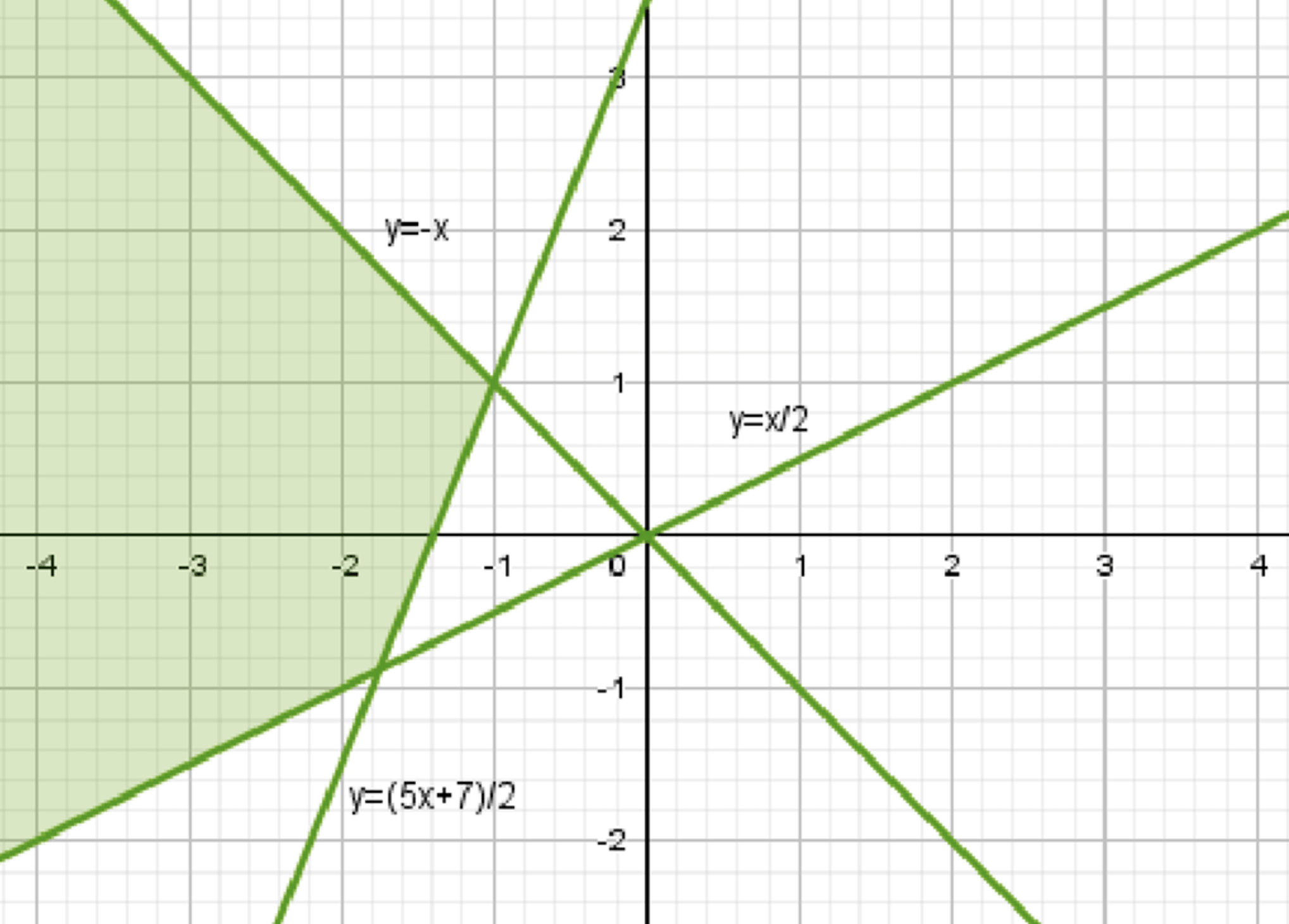
г) Дана система неравенств:
\( \begin{cases}
x — y \geq 2x \\
x + y \leq 3y \\
5x \leq 2y — 7
\end{cases} \)
Рассмотрим первое неравенство:
\( x — y \geq 2x \)
Выразим \( y \):
\( y \leq -x \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & 0 & -2 \\
\end{array}
\]
График первого неравенства представляет собой прямую \( y = -x \), ниже которой лежат все точки, удовлетворяющие неравенству.
Рассмотрим второе неравенство:
\( x + y \leq 3y \)
Выразим \( y \):
\( 2y \geq x \)
\( y \geq \frac{1}{2}x \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & 0 & 2 \\
\hline
y & 0 & 1 \\
\end{array}
\]
График второго неравенства представляет собой прямую \( y = \frac{1}{2}x \), выше которой лежат все точки, удовлетворяющие неравенству.
Рассмотрим третье неравенство:
\( 5x \leq 2y — 7 \)
Выразим \( y \):
\( 2y \geq 5x + 7 \)
\( y \geq \frac{5}{2}x + \frac{7}{2} \)
Для построения графика определим две точки:
\[
\begin{array}{c|c|c}
x & -3 & 1 \\
\hline
y & -4 & 6 \\
\end{array}
\]
График третьего неравенства представляет собой прямую \( y = \frac{5}{2}x + \frac{7}{2} \), выше которой лежат все точки, удовлетворяющие неравенству.
Множество точек:
Множество точек, удовлетворяющих системе неравенств, находится в области пересечения трех полуплоскостей.