Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.19 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( \sqrt{3x — y — 1} < \sqrt{2x + y — 1} \);
б) \( \sqrt{1 — y} \le \sqrt{1 — 2x^2} \);
в) \( \sqrt{x + y — 1} > \sqrt{2x — y} \);
г) \( \sqrt{y^2 — 1} \ge \sqrt{2x — 1} \)
Построить множество точек координатной плоскости, удовлетворяющих неравенству:
а) \( \sqrt{3x — y — 1} < \sqrt{2x + y — 1} \);
\( 3x — y — 1 < 2x + y — 1 \); \( 2y > x \);
\( y > \frac{1}{2}x \);
| \( x \) | 0 | 2 |
|---|---|---|
| \( y \) | 0 | 1 |
Выражение имеет смысл при:
\( 3x — y — 1 \ge 0 \);
\( y \le 3x — 1 \);
| \( x \) | 0 | 1 |
|---|---|---|
| \( y \) | -1 | 2 |
Множество точек:
б) \( \sqrt{1 — y} \le \sqrt{1 — 2x^2} \);
\( 1 — y \le 1 — 2x^2 \);
\( y \ge 2x^2 \);
| \( x \) | 0 | 1 | 2 |
|---|---|---|---|
| \( y \) | 0 | 2 | 8 |
Выражение имеет смысл при:
\( 1 — y \ge 0 \);
\( y \le 1 \);
Множество точек:
в) \( \sqrt{x + y — 1} > \sqrt{2x — y} \);
\( x + y — 1 > 2x — y \);
\( 2y > x + 1 \);
\( y > \frac{1}{2}x + \frac{1}{2} \);
| \( x \) | 1 | 3 |
|---|---|---|
| \( y \) | 1 | 2 |
Выражение имеет смысл при:
\( 2x — y \ge 0 \);
\( y \le 2x \);
| \( x \) | 0 | 1 |
|---|---|---|
| \( y \) | 0 | 2 |
Множество точек:
г) \( \sqrt{y^2 — 1} \ge \sqrt{2x — 1} \);
\( y^2 — 1 \ge 2x — 1 \);
\( 2x \le y^2 \);
\( x \le \frac{1}{2}y^2 \);
| \( x \) | 0 | 2 | 8 |
|---|---|---|---|
| \( y \) | 0 | 2 | 4 |
Выражение имеет смысл при:
\( 2x — 1 \ge 0 \);
\( 2x \ge 1 \);
\( x \ge \frac{1}{2} \);
Множество точек:
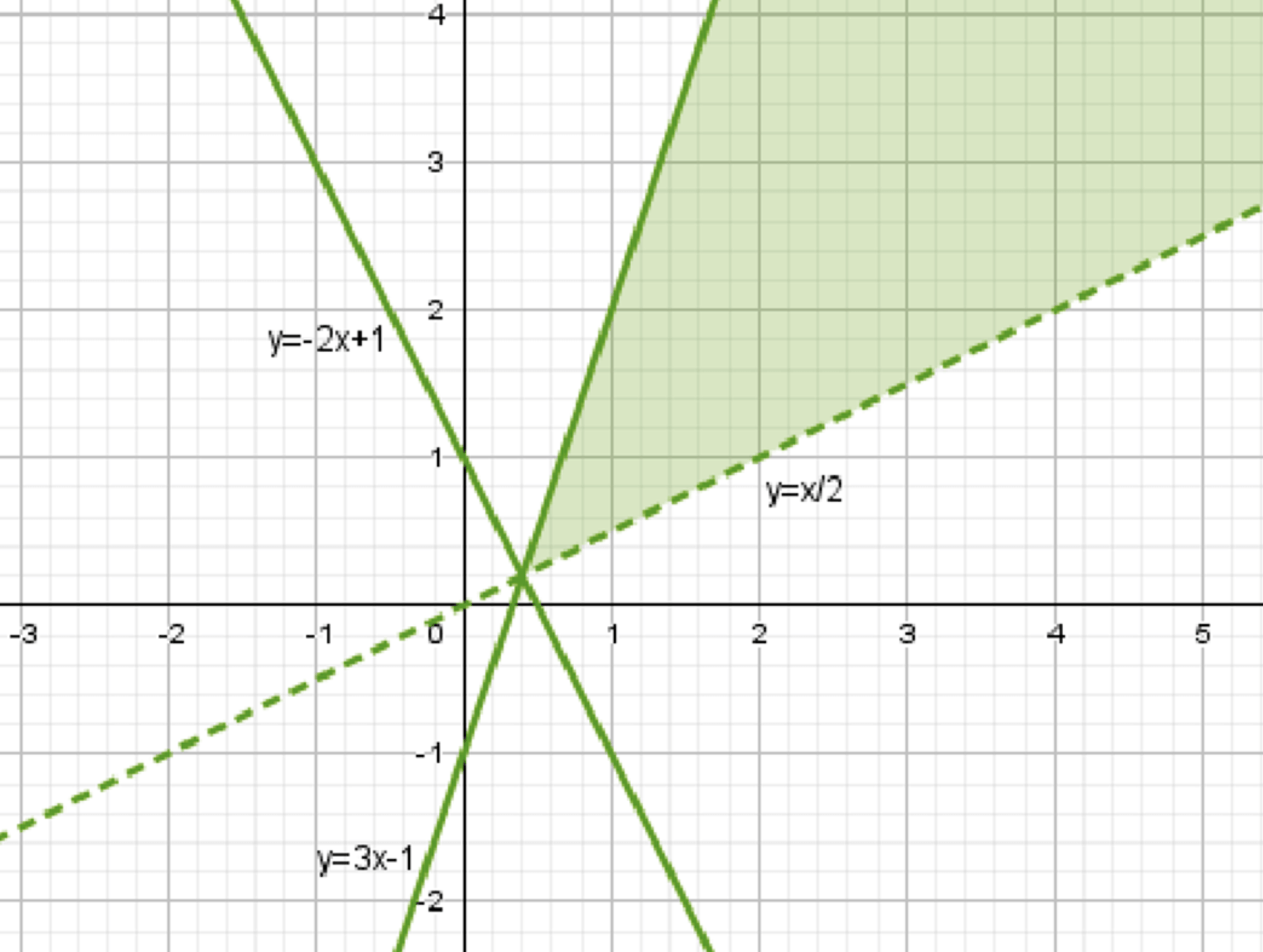
а) \( \sqrt{3x — y — 1} < \sqrt{2x + y — 1} \)
1. Уберем корни, так как подкоренные выражения положительны:
\( 3x — y — 1 < 2x + y — 1 \)
Приведем подобные:
\( 3x — 2x — y — y — 1 + 1 < 0 \)
\( x — 2y < 0 \)
Или в виде системы:
\( 2y > x \)
\( y > \frac{1}{2}x \)
Графически это прямые \( y = \frac{1}{2}x \) и \( y = \frac{1}{2}x \), область выше них.
2. Найдем область определения:
\( 3x — y — 1 \ge 0 \)
\( y \le 3x — 1 \)
Это прямая \( y = 3x — 1 \), область ниже нее.
3. Построим таблицу значений:
| \( x \) | 0 | 2 |
|---|---|---|
| \( y \) | 0 | 1 |
Область решения: пересечение областей выше прямых \( y = \frac{1}{2}x \), \( y = 3x — 1 \).
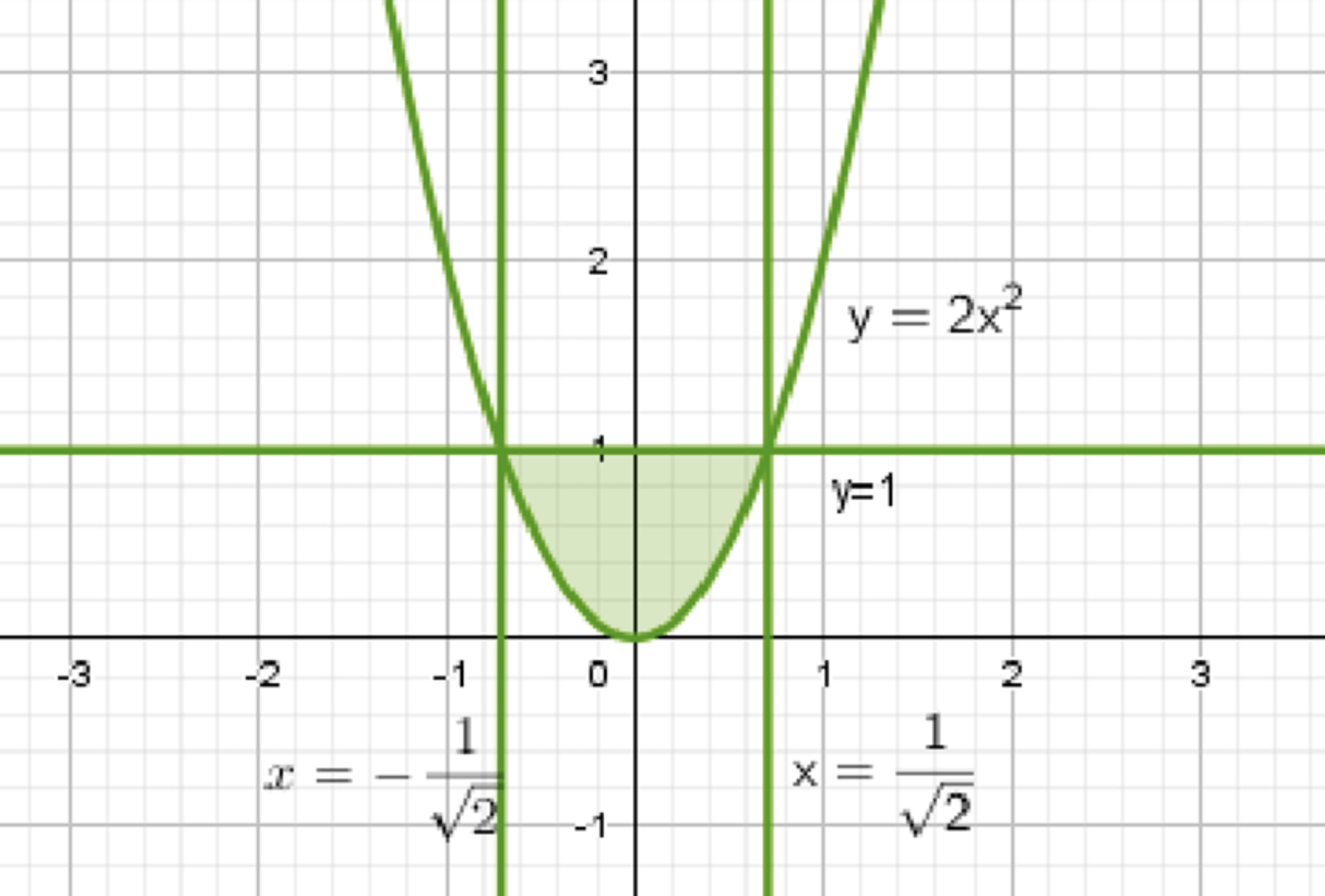
б) \( \sqrt{1 — y} \le \sqrt{1 — 2x^2} \)
1. Уберем корни:
\( 1 — y \le 1 — 2x^2 \)
Приведем подобные:
\( 1 — 1 — y + 2x^2 \le 0 \)
\( y \ge 2x^2 \)
Графически это парабола \( y = 2x^2 \), область выше нее.
2. Найдем область определения:
\( 1 — y \ge 0 \)
\( y \le 1 \)
Это прямая \( y = 1 \), область ниже нее.
3. Построим таблицу значений:
| \( x \) | 0 | 1 | 2 |
|---|---|---|---|
| \( y \) | 0 | 2 | 8 |
Область решения: пересечение областей выше параболы \( y = 2x^2 \), ниже прямой \( y = 1 \).
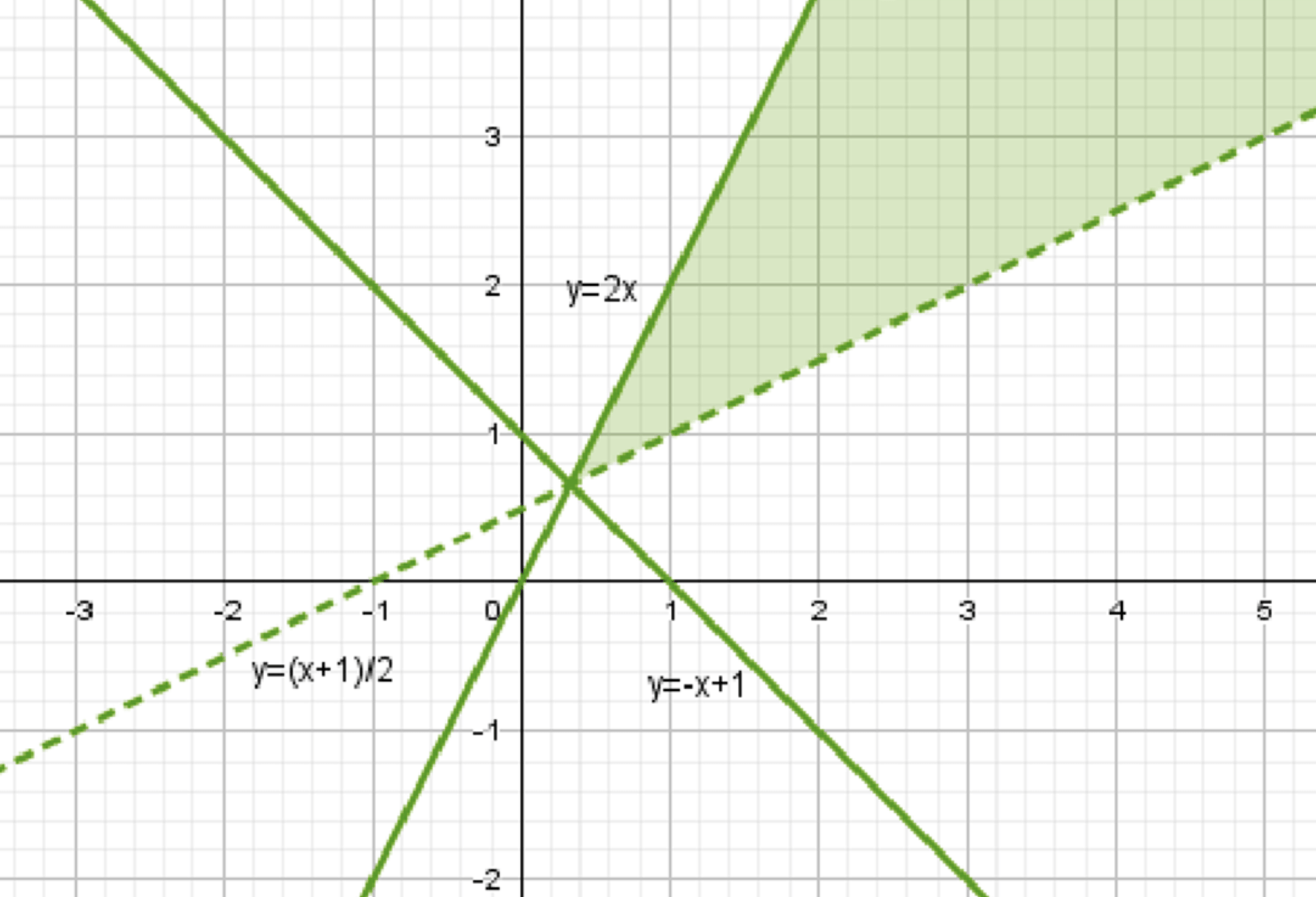
в) \( \sqrt{x + y — 1} > \sqrt{2x — y} \)
1. Уберем корни:
\( x + y — 1 > 2x — y \)
Приведем подобные:
\( x — 2x + y + y — 1 > 0 \)
\( 2y > x + 1 \)
\( y > \frac{1}{2}x + \frac{1}{2} \)
Графически это прямая \( y = \frac{1}{2}x + \frac{1}{2} \), область выше нее.
2. Найдем область определения:
\( 2x — y \ge 0 \)
\( y \le 2x \)
Это прямая \( y = 2x \), область ниже нее.
3. Построим таблицу значений:
| \( x \) | 1 | 3 |
|---|---|---|
| \( y \) | 1 | 2 |
Область решения: пересечение областей выше прямой \( y = \frac{1}{2}x + \frac{1}{2} \), ниже прямой \( y = 2x \).
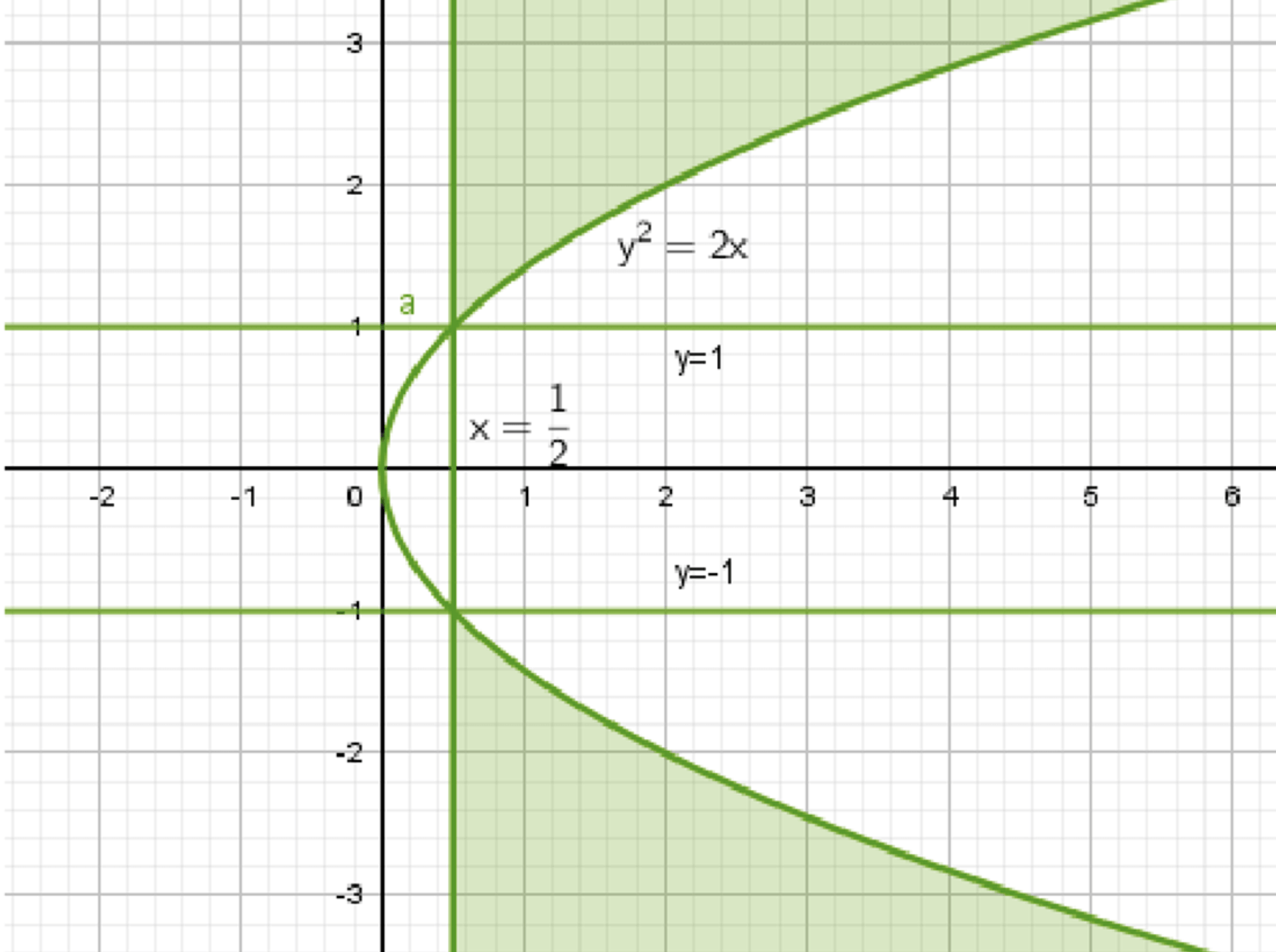
г) \( \sqrt{y^2 — 1} \ge \sqrt{2x — 1} \)
1. Уберем корни:
\( y^2 — 1 \ge 2x — 1 \)
Приведем подобные:
\( y^2 — 2x \ge 0 \)
\( 2x \le y^2 \)
\( x \le \frac{1}{2}y^2 \)
Графически это парабола \( x = \frac{1}{2}y^2 \), область слева от нее.
2. Найдем область определения:
\( 2x — 1 \ge 0 \)
\( x \ge \frac{1}{2} \)
Это вертикальная прямая \( x = \frac{1}{2} \), область справа от нее.
3. Построим таблицу значений:
| \( x \) | 0 | 2 | 8 |
|---|---|---|---|
| \( y \) | 0 | 2 | 4 |
Область решения: пересечение областей слева от параболы \( x = \frac{1}{2}y^2 \), справа от прямой \( x = \frac{1}{2} \).