Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.20 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( xy \leq 2 \)
б) \( y < \frac{2}{|x|} \)
в) \( |x| \cdot y < 2 \)
г) \( |x| < \frac{2}{y} \)
а) \( xy \leq 2 \)
Построить множество точек координатной плоскости, удовлетворяющих неравенству:
\( xy \leq 2 \)
Если \( x > 0 \), тогда:
\( y \leq \frac{2}{x} \)
Если \( x < 0 \), тогда:
\( y \geq \frac{2}{x} \)
Если \( x = 0 \), тогда:
\( 0 \leq 2 \)
\( y \in R \)
Координаты некоторых точек:
\( x \): \( 0.5, 1, 2 \)
\( y \): \( 4, 2, 1 \)
Множество точек:
б) \( y < \frac{2}{|x|} \)
Если \( x > 0 \), тогда:
\( y < \frac{2}{x} \)
Выражение имеет смысл при:
\( x \neq 0 \)
Координаты некоторых точек:
\( x \): \( 0.5, 1, 2 \)
\( y \): \( 4, 2, 1 \)
Множество симметрично относительно оси ординат:
в) \( |x| \cdot y < 2 \)
Если \( x > 0 \), тогда:
\( xy < 2 \)
\( y < \frac{2}{x} \)
Если \( x = 0 \), тогда:
\( 0 < 2 \)
\( y \in R \)
Координаты некоторых точек:
\( x \): \( 0.5, 1, 2 \)
\( y \): \( 4, 2, 1 \)
Множество симметрично относительно оси ординат:
г) \( |x| < \frac{2}{y} \)
Если \( x > 0 \) и \( y > 0 \), тогда:
\( xy < 2 \)
\( y < \frac{2}{x} \)
Неравенство имеет решения при:
\( \frac{2}{y} \geq 0 \)
\( y > 0 \)
Координаты некоторых точек:
\( x \): \( 0.5, 1, 2 \)
\( y \): \( 4, 2, 1 \)
Множество симметрично относительно оси ординат:
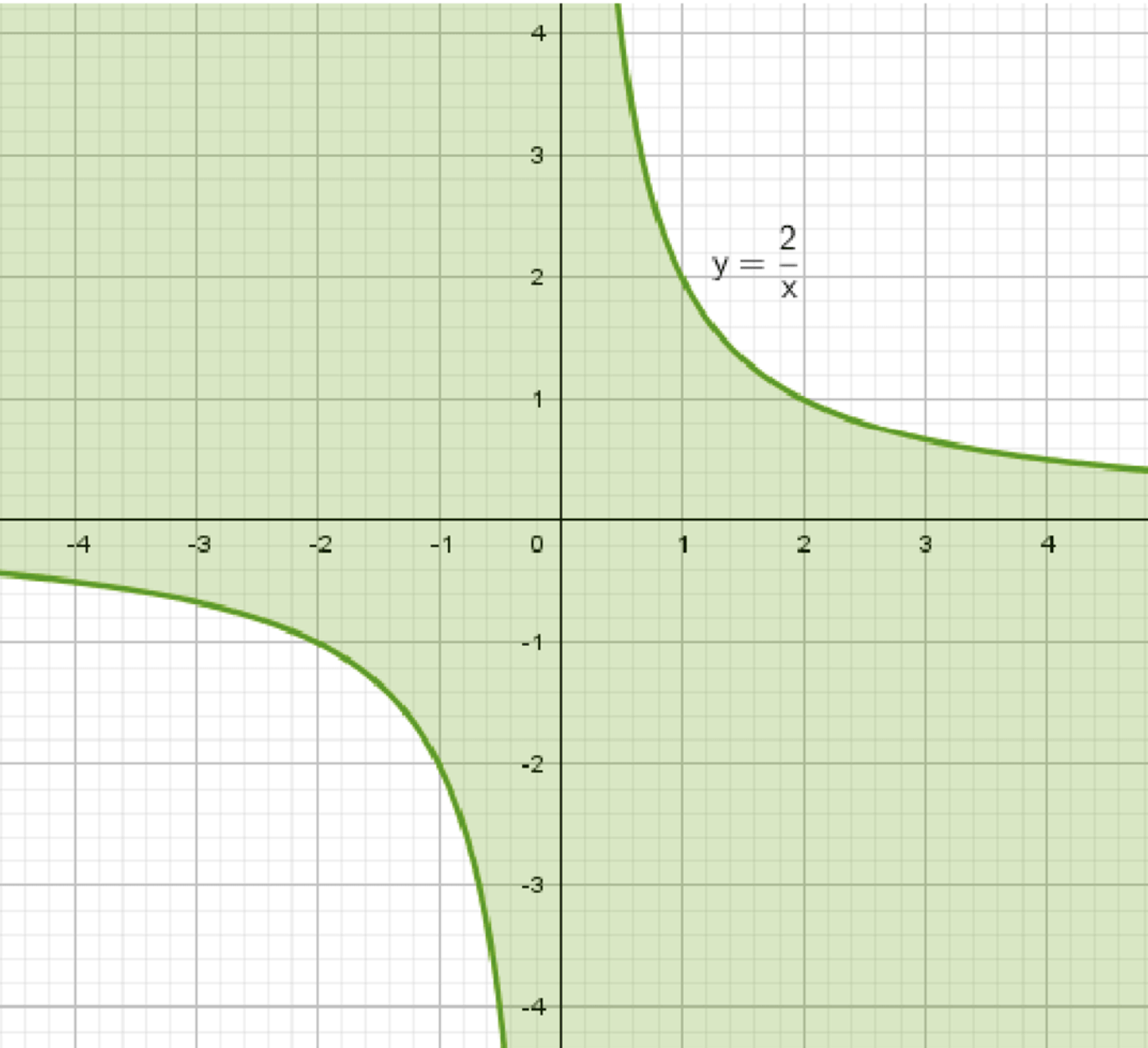
а) Множество точек, удовлетворяющих неравенству \( xy \leq 2 \)
Рассмотрим неравенство \( xy \leq 2 \), где \( x \) и \( y \) — переменные, которые могут принимать любые значения из множества действительных чисел.
Случай 1: \( x > 0 \)
Если \( x > 0 \), то можно разделить обе части неравенства на \( x \) (так как \( x > 0 \), знак неравенства не изменится):
\( y \leq \frac{2}{x} \)
Графически это соответствует ветви гиперболы \( y = \frac{2}{x} \), расположенной в первой координатной четверти. Все точки ниже этой гиперболы удовлетворяют неравенству.
Случай 2: \( x < 0 \)
Если \( x < 0 \), то при делении обеих частей неравенства на \( x \) знак неравенства изменится на противоположный:
\( y \geq \frac{2}{x} \)
Графически это соответствует ветви гиперболы \( y = \frac{2}{x} \), расположенной в третьей координатной четверти. Все точки выше этой гиперболы удовлетворяют неравенству.
Случай 3: \( x = 0 \)
Если \( x = 0 \), то произведение \( xy \) равно нулю. Подставим \( x = 0 \) в исходное неравенство:
\( 0 \leq 2 \)
Это всегда верно, поэтому \( y \) может принимать любое значение из множества действительных чисел \( y \in \mathbb{R} \).
Графически это соответствует вертикальной линии \( x = 0 \), покрывающей всю ось ординат.
Координаты некоторых точек:
\( x \) | \( 0.5 \) | \( 1 \) | \( 2 \) |
|---|---|---|---|
| \( y \) | \( 4 \) | \( 2 \) | \( 1 \) |
График состоит из двух ветвей гиперболы \( y = \frac{2}{x} \), расположенных в первой и третьей четвертях, а также вертикальной линии \( x = 0 \), покрывающей ось ординат.
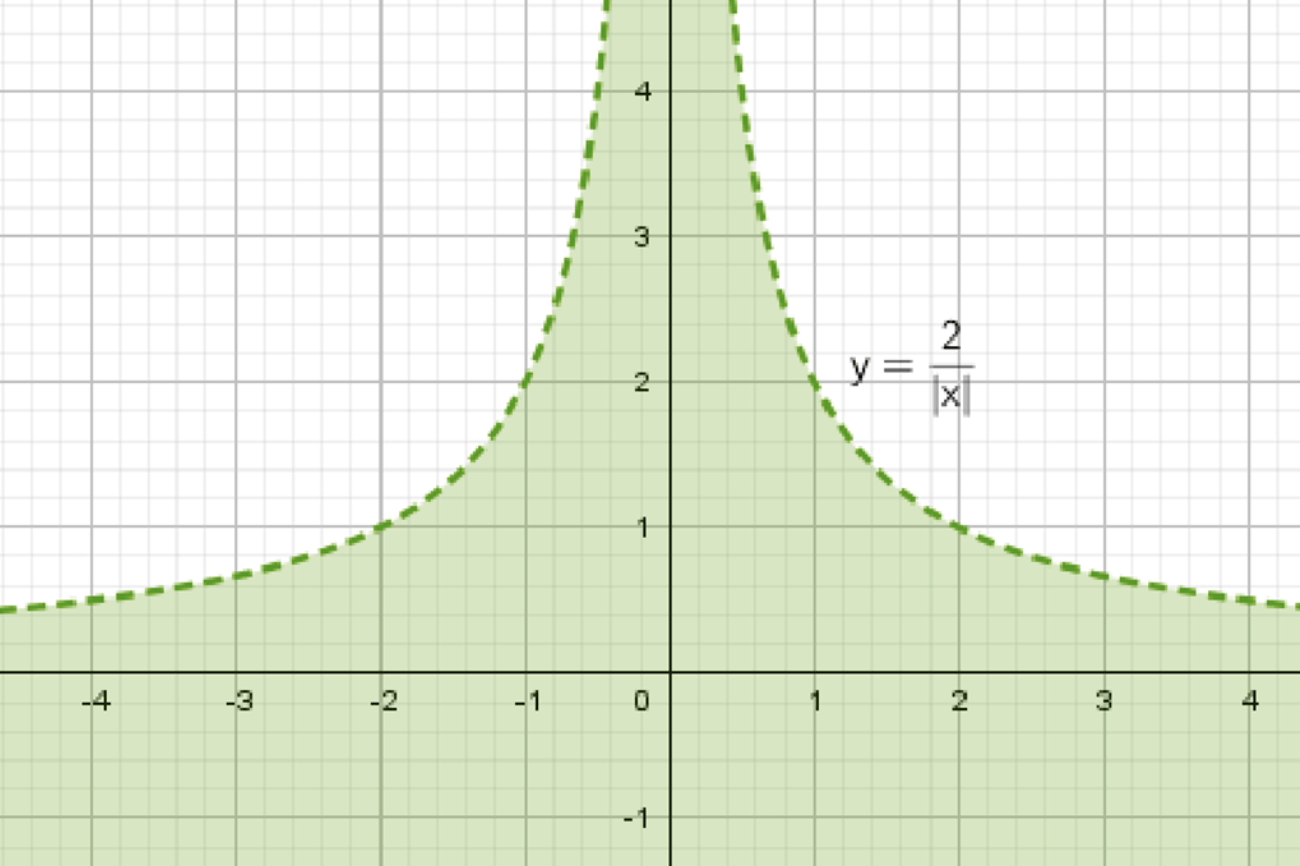
б) Множество точек, удовлетворяющих неравенству \( y < \frac{2}{|x|} \)
Рассмотрим неравенство \( y < \frac{2}{|x|} \), где \( x \neq 0 \) (так как знаменатель дроби не может быть равен нулю).
Случай 1: \( x > 0 \)
Если \( x > 0 \), то модуль \( x \) равен самому \( x \). Следовательно, неравенство принимает вид:
\( y < \frac{2}{x} \)
Графически это соответствует ветви гиперболы \( y = \frac{2}{x} \), расположенной в первой координатной четверти. Все точки ниже этой гиперболы удовлетворяют неравенству.
Случай 2: \( x < 0 \)
Если \( x < 0 \), то модуль \( x \) равен \( -x \). Следовательно, неравенство принимает вид:
\( y < \frac{-2}{x} \)
Графически это соответствует ветви гиперболы \( y = \frac{2}{x} \), расположенной во второй и четвёртой четвертях. Все точки ниже этой гиперболы удовлетворяют неравенству.
Координаты некоторых точек:
\( x \) | \( 0.5 \) | \( 1 \) | \( 2 \) |
|---|---|---|---|
| \( y \) | \( 4 \) | \( 2 \) | \( 1 \) |
График состоит из двух ветвей гиперболы \( y = \frac{2}{x} \), расположенных симметрично относительно оси ординат.
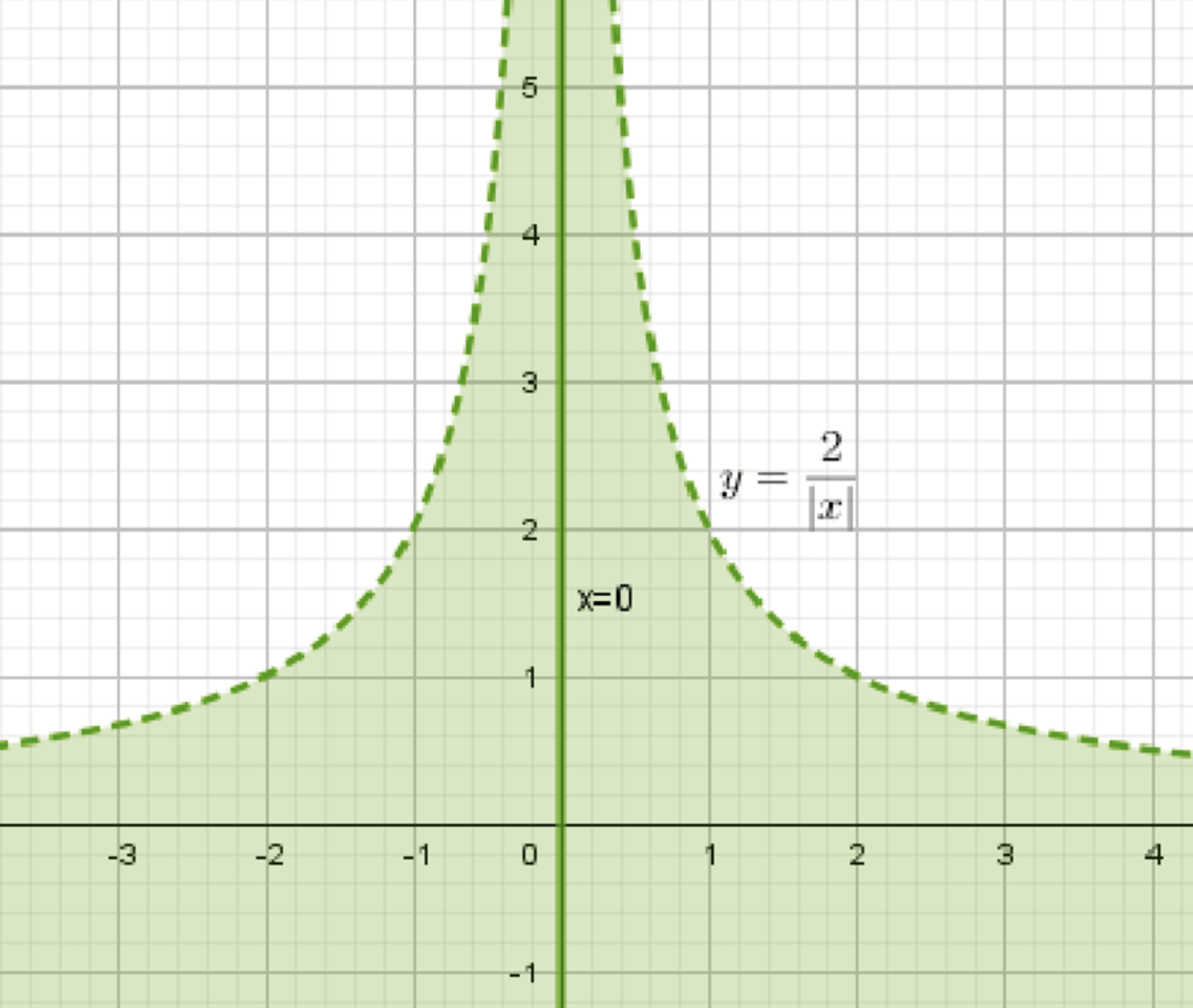
в) Множество точек, удовлетворяющих неравенству \( |x| \cdot y < 2 \)
Рассмотрим неравенство \( |x| \cdot y < 2 \), где \( x \) и \( y \) — переменные, которые могут принимать любые значения из множества действительных чисел.
Случай 1: \( x > 0 \)
Если \( x > 0 \), то модуль \( x \) равен самому \( x \). Следовательно, неравенство принимает вид:
\( xy < 2 \)
Разделим обе части неравенства на \( x \) (так как \( x > 0 \), знак неравенства не изменится):
\( y < \frac{2}{x} \)
Графически это соответствует ветви гиперболы \( y = \frac{2}{x} \), расположенной в первой координатной четверти. Все точки ниже этой гиперболы удовлетворяют неравенству.
Случай 2: \( x = 0 \)
Если \( x = 0 \), то произведение \( |x| \cdot y \) равно нулю. Подставим \( x = 0 \) в исходное неравенство:
\( 0 < 2 \)
Это всегда верно, поэтому \( y \) может принимать любое значение из множества действительных чисел \( y \in \mathbb{R} \).
Графически это соответствует вертикальной линии \( x = 0 \), покрывающей ось ординат.
Координаты некоторых точек:
\( x \) | \( 0.5 \) | \( 1 \) | \( 2 \) |
|---|---|---|---|
| \( y \) | \( 4 \) | \( 2 \) | \( 1 \) |
График состоит из двух ветвей гиперболы \( y = \frac{2}{x} \), расположенных симметрично относительно оси ординат, а также вертикальной линии \( x = 0 \), покрывающей ось ординат.
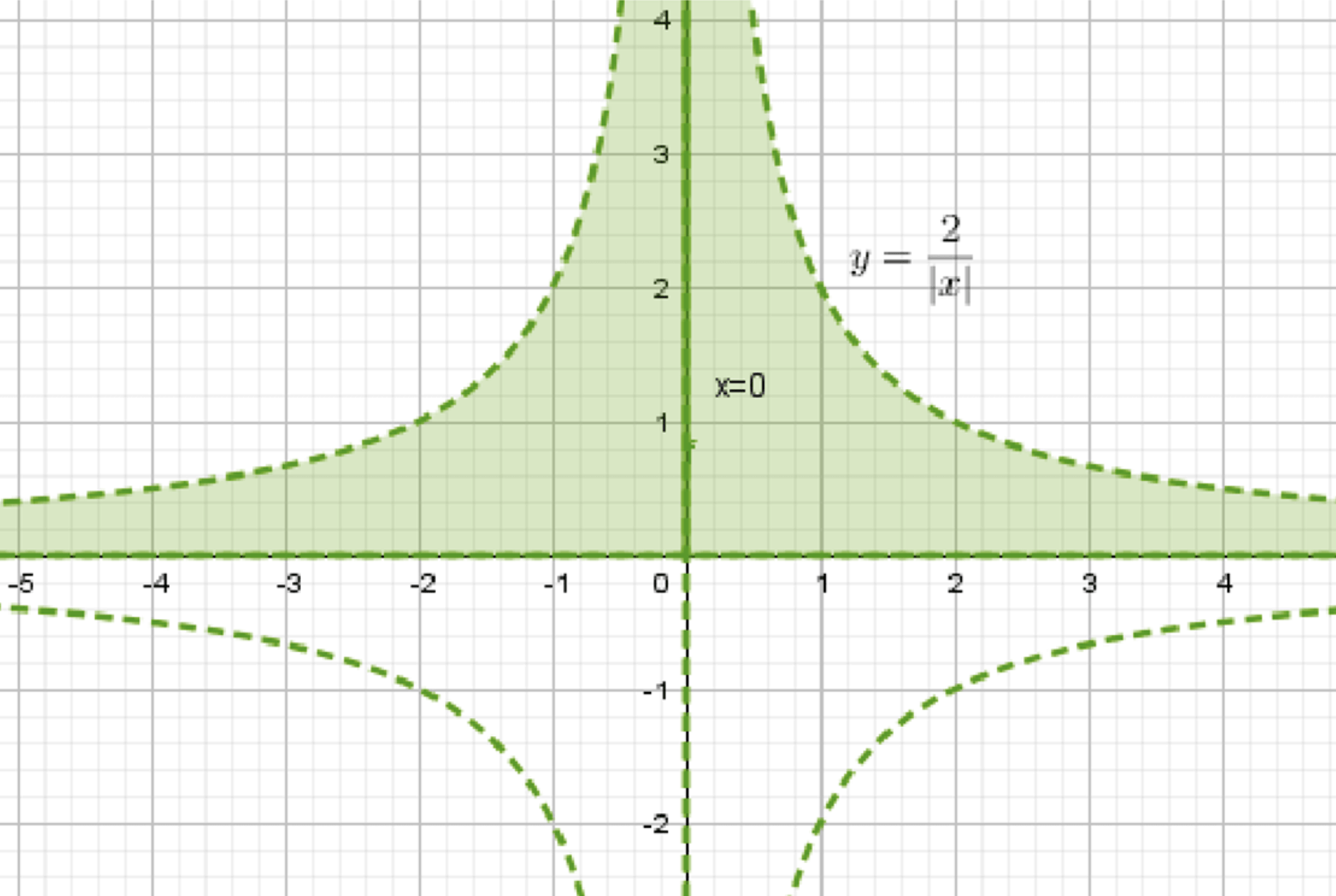
г) Множество точек, удовлетворяющих неравенству \( |x| < \frac{2}{y} \)
Рассмотрим неравенство \( |x| < \frac{2}{y} \), где \( x \) и \( y \) — переменные, которые могут принимать любые значения из множества действительных чисел.
Случай 1: \( x > 0 \) и \( y > 0 \)
Если \( x > 0 \) и \( y > 0 \), то модуль \( x \) равен самому \( x \). Следовательно, неравенство принимает вид:
\( x < \frac{2}{y} \)
Умножим обе части на \( y \) (так как \( y > 0 \), знак неравенства не изменится):
\( xy < 2 \)
Разделим обе части на \( x \) (так как \( x > 0 \), знак неравенства не изменится):
\( y < \frac{2}{x} \)
Графически это соответствует ветви гиперболы \( y = \frac{2}{x} \), расположенной в первой координатной четверти. Все точки ниже этой гиперболы удовлетворяют неравенству.
Случай 2: Условие существования
Для того чтобы выражение \( \frac{2}{y} \) имело смысл, знаменатель \( y \) должен быть положительным:
\( \frac{2}{y} \geq 0 \)
\( y > 0 \)
Координаты некоторых точек:
\( x \) | \( 0.5 \) | \( 1 \) | \( 2 \) |
|---|---|---|---|
| \( y \) | \( 4 \) | \( 2 \) | \( 1 \) |
График состоит из двух ветвей гиперболы \( y = \frac{2}{x} \), расположенных симметрично относительно оси ординат, при условии \( y > 0 \).