Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.21 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( |x| + |y| \leq 4 \)
б) \( 2|x| + 3|y| \leq 6 \)
а) \( |x| + |y| \leq 4 \)
Для \( x > 0, y > 0 \):
\( x + y \leq 4 \)
\( y \leq -x + 4 \)
Таблица точек:
\( x \) | \( y \) |
|---|---|
| \( 0 \) | \( 4 \) |
| \( 4 \) | \( 0 \) |
Множество симметрично относительно осей координат.
б) \( 2|x| + 3|y| \leq 6 \)
Для \( x > 0, y > 0 \):
\( 2x + 3y \leq 6 \)
\( 3y \leq -2x + 6 \)
\( y \leq -\frac{2}{3}x + 2 \)
Таблица точек:
\( x \) | \( y \) |
|---|---|
| \( 0 \) | \( 2 \) |
| \( 3 \) | \( 0 \) |
Множество симметрично относительно осей координат.
а) \( |x| + |y| \leq 4 \)
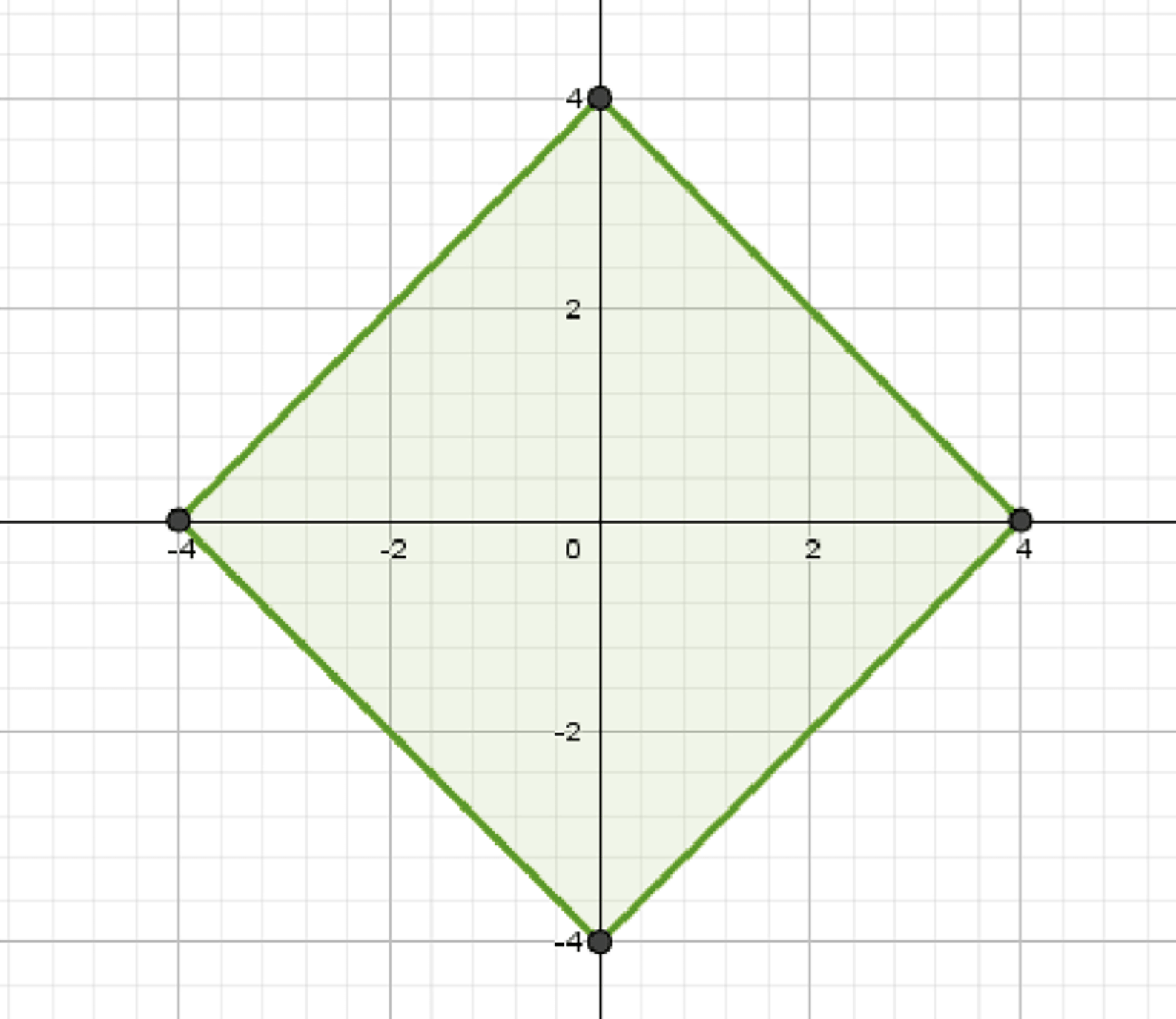
Рассмотрим множество точек координатной плоскости, удовлетворяющих неравенству \( |x| + |y| \leq 4 \). Это множество представляет собой ромб, стороны которого параллельны осям координат.
Неравенство \( |x| + |y| \leq 4 \) можно разбить на четыре случая в зависимости от знаков \( x \) и \( y \):
Случай 1: \( x > 0, y > 0 \)
В этом случае модуль \( |x| \) равен \( x \), а модуль \( |y| \) равен \( y \). Подставим в неравенство:
\( x + y \leq 4 \)
Выразим \( y \):
\( y \leq -x + 4 \)
График этой функции — прямая, проходящая через точки \( (0, 4) \) и \( (4, 0) \). Все точки ниже этой прямой удовлетворяют неравенству.
Случай 2: \( x > 0, y < 0 \)
В этом случае модуль \( |x| \) равен \( x \), а модуль \( |y| \) равен \( -y \). Подставим в неравенство:
\( x — y \leq 4 \)
Выразим \( y \):
\( y \geq x — 4 \)
График этой функции — прямая, проходящая через точки \( (0, -4) \) и \( (4, 0) \). Все точки выше этой прямой удовлетворяют неравенству.
Случай 3: \( x < 0, y > 0 \)
В этом случае модуль \( |x| \) равен \( -x \), а модуль \( |y| \) равен \( y \). Подставим в неравенство:
\( -x + y \leq 4 \)
Выразим \( y \):
\( y \leq x + 4 \)
График этой функции — прямая, проходящая через точки \( (0, 4) \) и \( (-4, 0) \). Все точки ниже этой прямой удовлетворяют неравенству.
Случай 4: \( x < 0, y < 0 \)
В этом случае модуль \( |x| \) равен \( -x \), а модуль \( |y| \) равен \( -y \). Подставим в неравенство:
\( -x — y \leq 4 \)
Выразим \( y \):
\( y \geq -x — 4 \)
График этой функции — прямая, проходящая через точки \( (0, -4) \) и \( (-4, 0) \). Все точки выше этой прямой удовлетворяют неравенству.
Таблица точек:
\( x \) | \( y \) |
|---|---|
| \( 0 \) | \( 4 \) |
| \( 4 \) | \( 0 \) |
| \( 0 \) | \( -4 \) |
| \( -4 \) | \( 0 \) |
График множества точек — ромб с вершинами в точках \( (0, 4) \), \( (4, 0) \), \( (0, -4) \), \( (-4, 0) \). Множество симметрично относительно осей координат.
б) \( 2|x| + 3|y| \leq 6 \)
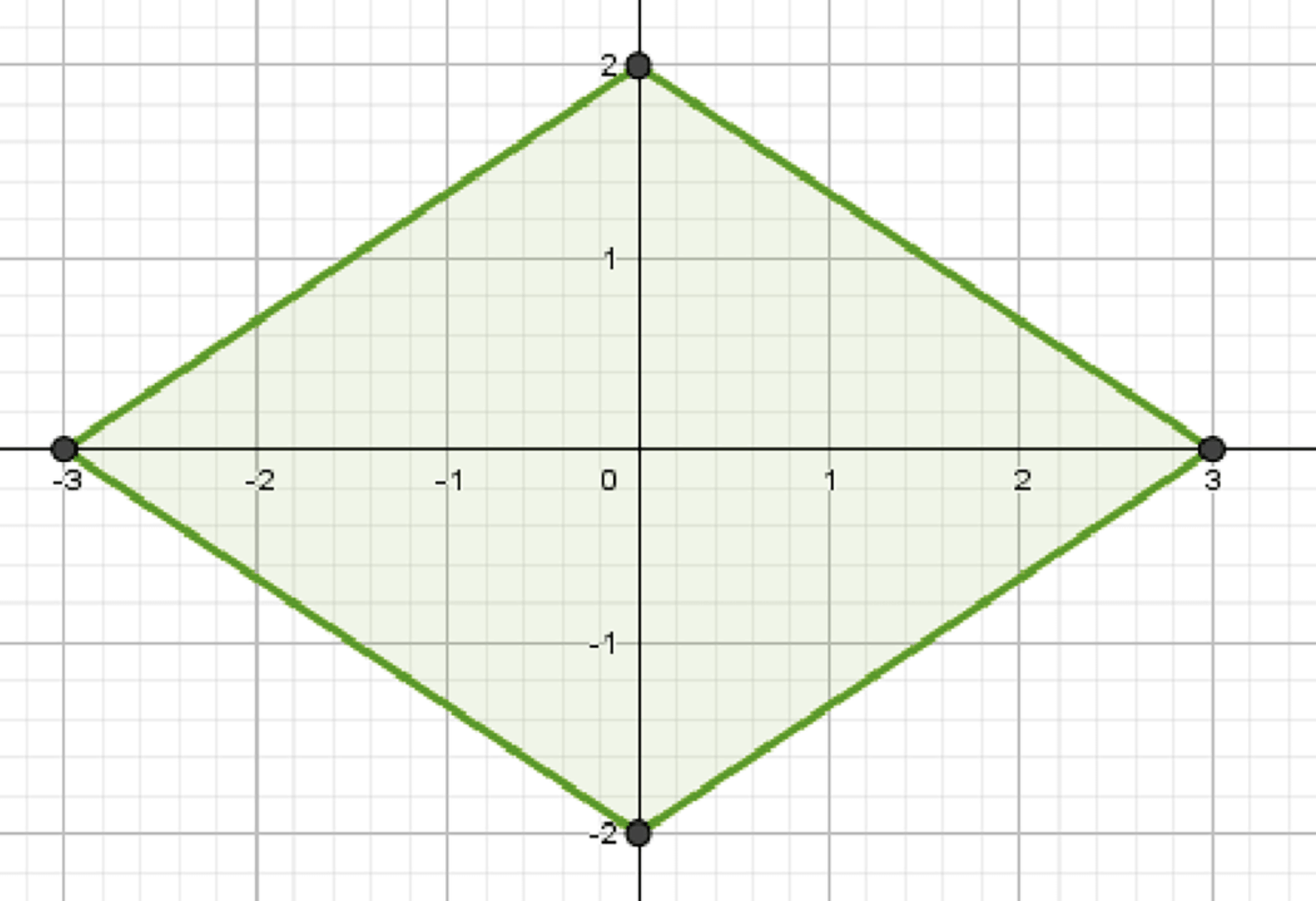
Рассмотрим множество точек координатной плоскости, удовлетворяющих неравенству \( 2|x| + 3|y| \leq 6 \). Это множество представляет собой четырехугольник, стороны которого параллельны координатным осям.
Неравенство \( 2|x| + 3|y| \leq 6 \) можно разбить на четыре случая в зависимости от знаков \( x \) и \( y \):
Случай 1: \( x > 0, y > 0 \)
В этом случае модуль \( |x| \) равен \( x \), а модуль \( |y| \) равен \( y \). Подставим в неравенство:
\( 2x + 3y \leq 6 \)
Выразим \( y \):
\( 3y \leq -2x + 6 \)
\( y \leq -\frac{2}{3}x + 2 \)
График этой функции — прямая, проходящая через точки \( (0, 2) \) и \( (3, 0) \). Все точки ниже этой прямой удовлетворяют неравенству.
Случай 2: \( x > 0, y < 0 \)
В этом случае модуль \( |x| \) равен \( x \), а модуль \( |y| \) равен \( -y \). Подставим в неравенство:
\( 2x — 3y \leq 6 \)
Выразим \( y \):
\( -3y \leq -2x + 6 \)
\( y \geq \frac{2}{3}x — 2 \)
График этой функции — прямая, проходящая через точки \( (0, -2) \) и \( (3, 0) \). Все точки выше этой прямой удовлетворяют неравенству.
Случай 3: \( x < 0, y > 0 \)
В этом случае модуль \( |x| \) равен \( -x \), а модуль \( |y| \) равен \( y \). Подставим в неравенство:
\( -2x + 3y \leq 6 \)
Выразим \( y \):
\( 3y \leq 2x + 6 \)
\( y \leq \frac{2}{3}x + 2 \)
График этой функции — прямая, проходящая через точки \( (0, 2) \) и \( (-3, 0) \). Все точки ниже этой прямой удовлетворяют неравенству.
Случай 4: \( x < 0, y < 0 \)
В этом случае модуль \( |x| \) равен \( -x \), а модуль \( |y| \) равен \( -y \). Подставим в неравенство:
\( -2x — 3y \leq 6 \)
Выразим \( y \):
\( -3y \leq 2x + 6 \)
\( y \geq -\frac{2}{3}x — 2 \)
График этой функции — прямая, проходящая через точки \( (0, -2) \) и \( (-3, 0) \). Все точки выше этой прямой удовлетворяют неравенству.
Таблица точек:
\( x \) | \( y \) |
|---|---|
| \( 0 \) | \( 2 \) |
| \( 3 \) | \( 0 \) |
| \( 0 \) | \( -2 \) |
| \( -3 \) | \( 0 \) |
График множества точек — четырехугольник с вершинами в точках \( (0, 2) \), \( (3, 0) \), \( (0, -2) \), \( (-3, 0) \). Множество симметрично относительно осей координат.