Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.22 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \( \frac{4 — x^{2}}{2x + 3y — 6} \geq 0 \)
б) \( \frac{x^{2} + y^{2} — 4}{|x| + |y| — 2} \leq 0 \)
а) \( \frac{4 — x^{2}}{2x + 3y — 6} \geq 0 \)
Первая система неравенств:
\(
\begin{cases}
4 — x^{2} \geq 0 \\
2x + 3y — 6 > 0
\end{cases}
⇒
\begin{cases}
x^{2} \leq 4 \\
3y > -2x + 6
\end{cases}
⇒
\begin{cases}
-2 \leq x \leq 2 \\
y > -\frac{2}{3}x + 2
\end{cases}
\)
Вторая система неравенств:
\(
\begin{cases}
4 — x^{2} \leq 0 \\
2x + 3y — 6 < 0
\end{cases}
⇒
\begin{cases}
x^{2} \geq 4 \\
y < -\frac{2}{3}x + 2
\end{cases}
\)
Множество решений:
б) \( \frac{x^{2} + y^{2} — 4}{|x| + |y| — 2} \leq 0 \)
Если \( x \geq 0 \) и \( y \geq 0 \), тогда:
\( \frac{x^{2} + y^{2} — 4}{x + y — 2} \leq 0 \)
Первая система неравенств:
\(
\begin{cases}
x^{2} + y^{2} — 4 \geq 0 \\
x + y — 2 < 0
\end{cases}
⇒
\begin{cases}
x^{2} + y^{2} \geq 4 \\
y < 2 — x
\end{cases}
\)
Вторая система неравенств:
\(
\begin{cases}
x^{2} + y^{2} — 4 \leq 0 \\
x + y — 2 > 0
\end{cases}
⇒
\begin{cases}
x^{2} + y^{2} \leq 4 \\
y > 2 — x
\end{cases}
\)
Множество симметрично относительно осей координат:
а) \( \frac{4 — x^{2}}{2x + 3y — 6} \geq 0 \)
Рассмотрим дробь \( \frac{4 — x^{2}}{2x + 3y — 6} \). Для выполнения условия \( \frac{4 — x^{2}}{2x + 3y — 6} \geq 0 \), числитель и знаменатель должны быть одного знака: либо оба положительные, либо оба отрицательные.
Первая система неравенств:
Числитель \( 4 — x^{2} \geq 0 \), знаменатель \( 2x + 3y — 6 > 0 \). Запишем систему:
\(
\begin{cases}
4 — x^{2} \geq 0 \\
2x + 3y — 6 > 0
\end{cases}
\)
Рассмотрим первое неравенство \( 4 — x^{2} \geq 0 \):
\( x^{2} \leq 4 \), откуда \( -2 \leq x \leq 2 \).
Рассмотрим второе неравенство \( 2x + 3y — 6 > 0 \):
\( 3y > -2x + 6 \), откуда \( y > -\frac{2}{3}x + 2 \).
Итак, первая система имеет вид:
\(
\begin{cases}
-2 \leq x \leq 2 \\
y > -\frac{2}{3}x + 2
\end{cases}
\)
Вторая система неравенств:
Числитель \( 4 — x^{2} \leq 0 \), знаменатель \( 2x + 3y — 6 < 0 \). Запишем систему:
\(
\begin{cases}
4 — x^{2} \leq 0 \\
2x + 3y — 6 < 0
\end{cases}
\)
Рассмотрим первое неравенство \( 4 — x^{2} \leq 0 \):
\( x^{2} \geq 4 \), откуда \( x \leq -2 \) или \( x \geq 2 \).
Рассмотрим второе неравенство \( 2x + 3y — 6 < 0 \):
\( 3y < -2x + 6 \), откуда \( y < -\frac{2}{3}x + 2 \).
Итак, вторая система имеет вид:
\(
\begin{cases}
x \leq -2 \text{ или } x \geq 2 \\
y < -\frac{2}{3}x + 2
\end{cases}
\)
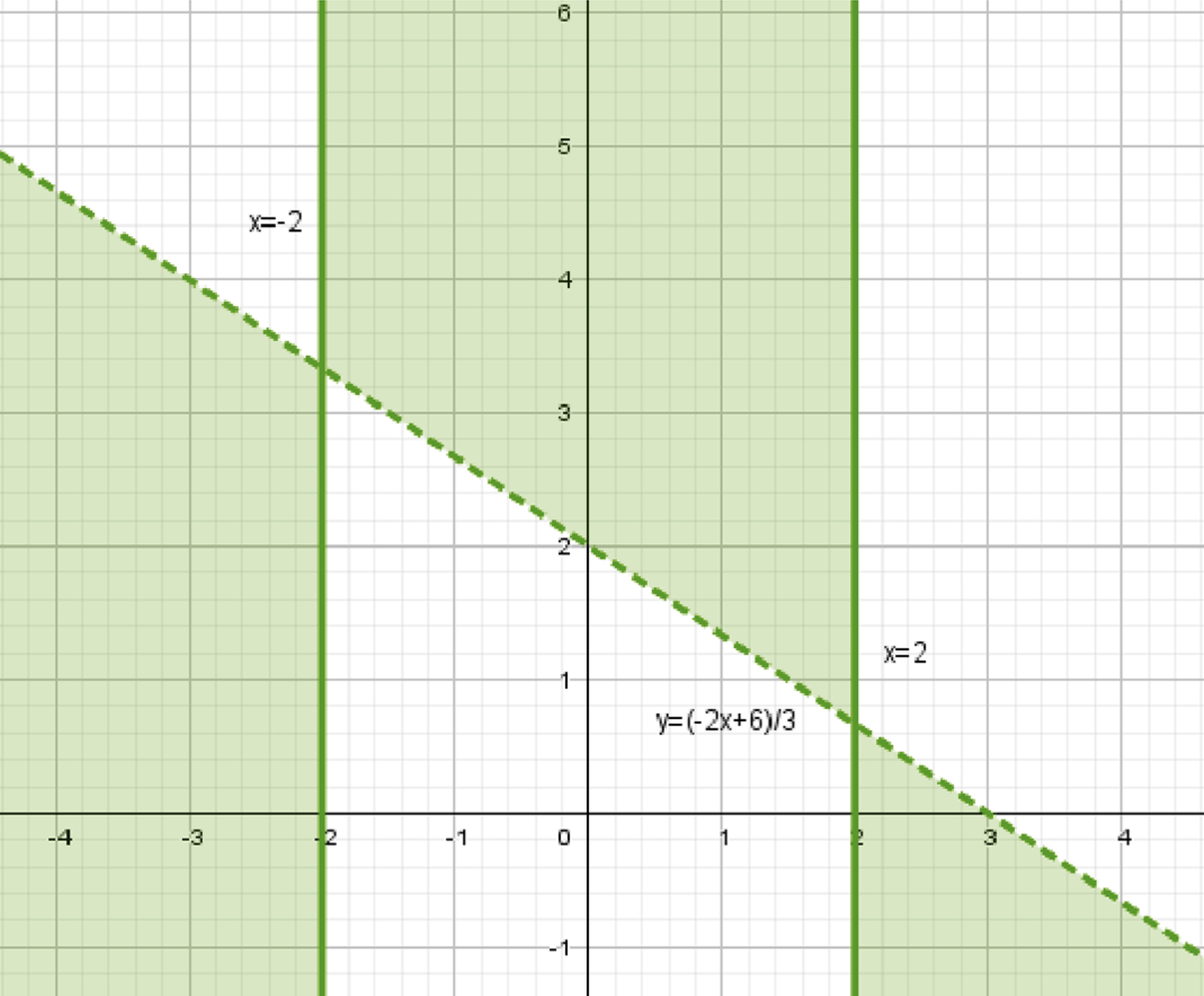
График множества решений:
На координатной плоскости множество решений состоит из двух областей:
- Первая область: точки внутри вертикальной полосы \( -2 \leq x \leq 2 \), расположенные выше прямой \( y = -\frac{2}{3}x + 2 \).
- Вторая область: точки вне полосы \( -2 \leq x \leq 2 \), расположенные ниже прямой \( y = -\frac{2}{3}x + 2 \).
б) \( \frac{x^{2} + y^{2} — 4}{|x| + |y| — 2} \leq 0 \)
Рассмотрим дробь \( \frac{x^{2} + y^{2} — 4}{|x| + |y| — 2} \). Для выполнения условия \( \frac{x^{2} + y^{2} — 4}{|x| + |y| — 2} \leq 0 \), числитель и знаменатель должны быть разных знаков: либо числитель отрицательный и знаменатель положительный, либо числитель положительный и знаменатель отрицательный.
Случай \( x \geq 0 \) и \( y \geq 0 \):
В этом случае модуль \( |x| \) равен \( x \), а модуль \( |y| \) равен \( y \). Дробь принимает вид:
\( \frac{x^{2} + y^{2} — 4}{x + y — 2} \leq 0 \)
Первая система неравенств:
Числитель \( x^{2} + y^{2} — 4 \geq 0 \), знаменатель \( x + y — 2 < 0 \). Запишем систему:
\(
\begin{cases}
x^{2} + y^{2} \geq 4 \\
x + y < 2
\end{cases}
\)
Первое неравенство \( x^{2} + y^{2} \geq 4 \) описывает внешнюю часть окружности с центром в начале координат и радиусом 2.
Второе неравенство \( x + y < 2 \) описывает полуплоскость ниже прямой \( x + y = 2 \).
Итак, эта система описывает область вне окружности радиуса 2, ниже прямой \( x + y = 2 \).
Вторая система неравенств:
Числитель \( x^{2} + y^{2} — 4 \leq 0 \), знаменатель \( x + y — 2 > 0 \). Запишем систему:
\(
\begin{cases}
x^{2} + y^{2} \leq 4 \\
x + y > 2
\end{cases}
\)
Первое неравенство \( x^{2} + y^{2} \leq 4 \) описывает внутреннюю часть окружности с центром в начале координат и радиусом 2.
Второе неравенство \( x + y > 2 \) описывает полуплоскость выше прямой \( x + y = 2 \).
Итак, эта система описывает область внутри окружности радиуса 2, выше прямой \( x + y = 2 \).
Симметрия:
Множество решений симметрично относительно осей координат, так как выражение \( |x| + |y| \) и \( x^{2} + y^{2} \) не зависят от знаков \( x \) и \( y \).
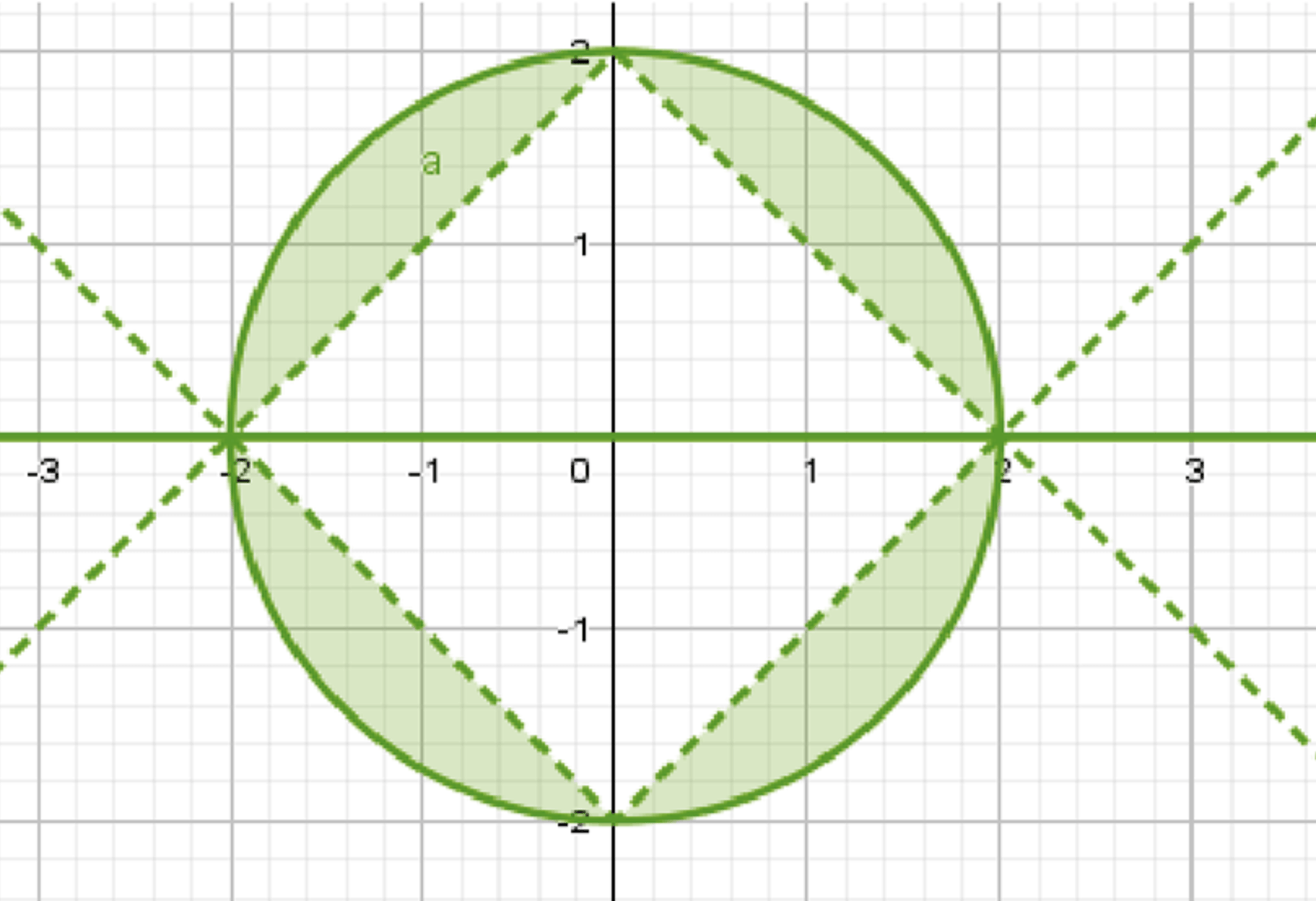
График множества решений:
На координатной плоскости множество решений состоит из четырех областей:
- Области вне окружности радиуса 2, расположенные ниже прямой \( x + y = 2 \).
- Области внутри окружности радиуса 2, расположенные выше прямой \( x + y = 2 \).