ГДЗ 10-11 Класс Номер 58.23 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Найдите площадь фигуры, заданной системой неравенств:

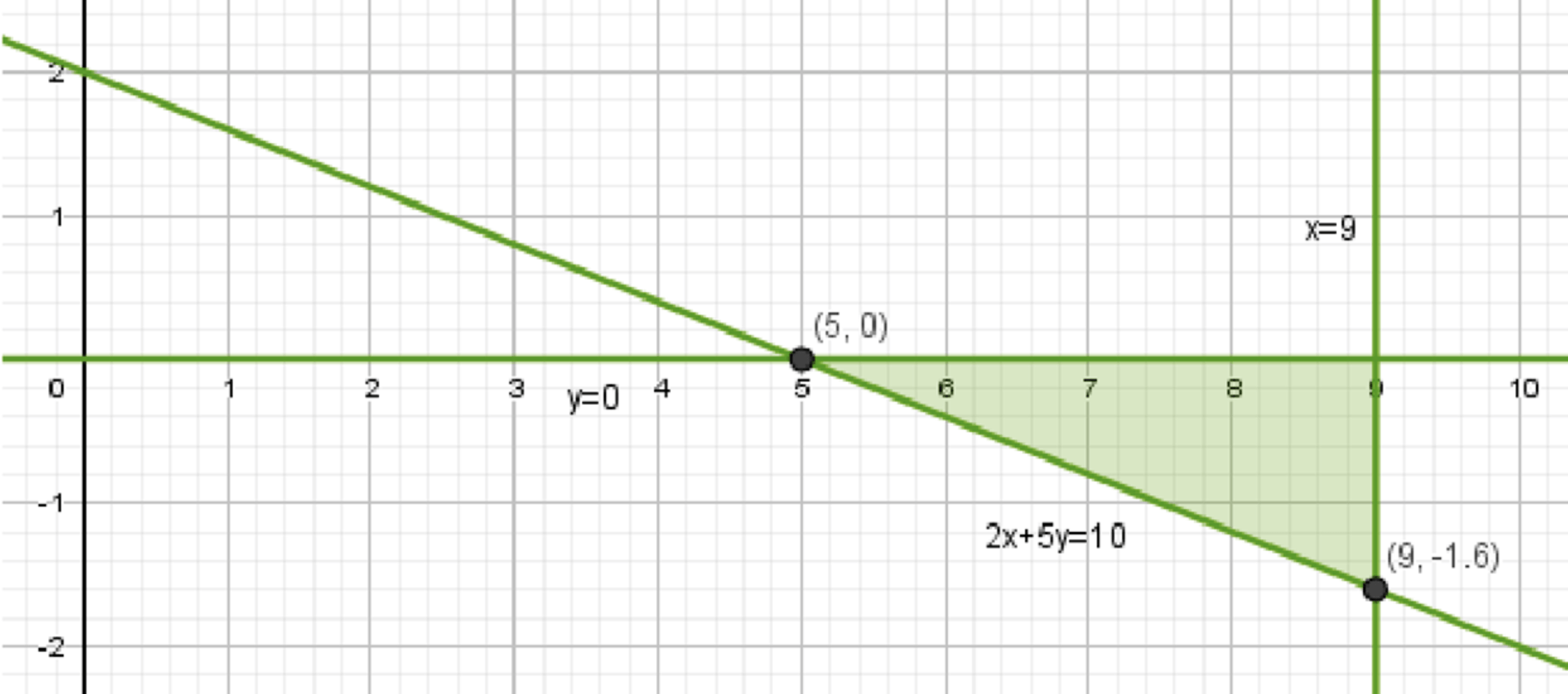
а) \( \begin{cases} x \le 9 \\ y \le 0 \\ 2x + 5y \ge 10 \end{cases} \);

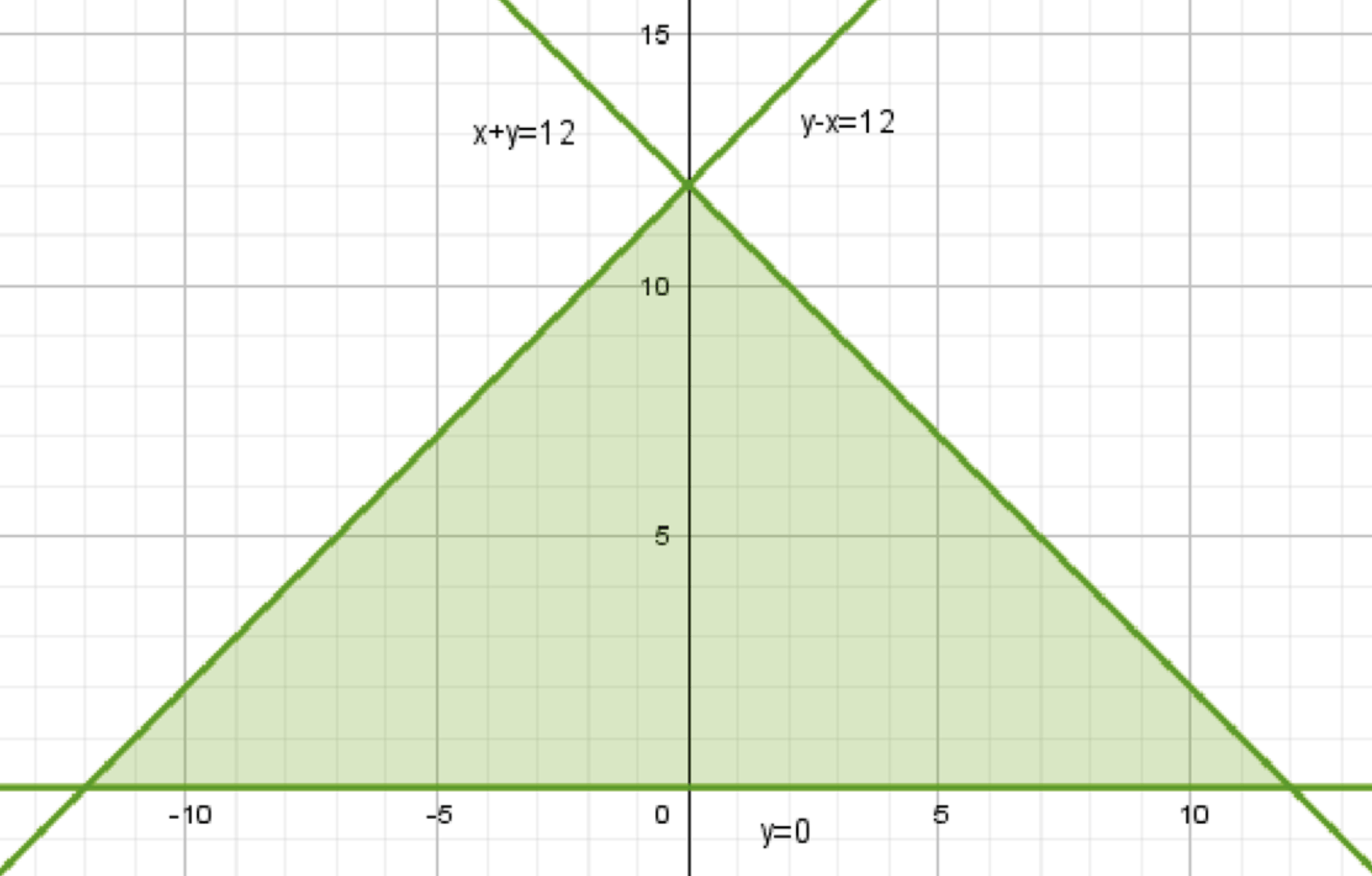
б) \( \begin{cases} x + y \le 12 \\ y — x \le 12 \\ y \ge 0 \end{cases} \)

Найти площадь фигуры, заданной системой неравенств:

а) \( \begin{cases} x \le 9 \\ y \le 0 \\ 2x + 5y \ge 10 \end{cases} \);
Третье неравенство:
\( 2x + 5y \ge 10 \);
\( 5y \ge -2x + 10 \);
\( y \ge -\frac{2}{5}x + 2 \);
Множество решений:

Точка пересечения первой и третьей прямой:
\( y(9) = -\frac{2}{5} \cdot 9 + 2 = -3,6 + 2 = -1,6 \);
Площадь искомой фигуры:
\( S = \frac{1}{2} \cdot (9 — 5) \cdot 1,6 = 0,8 \cdot 4 = 3,2 \);
Ответ: 3,2.

б) \( \begin{cases} x + y \le 12 \\ y — x \le 12 \\ y \ge 0 \end{cases} \);
Первое неравенство:
\( x + y \le 12 \);
\( y \le 12 — x \);
Второе неравенство:
\( y — x \le 12 \);
\( y \le x + 12 \);
Множество решений:

Площадь искомой фигуры:
\( S = \frac{1}{2} \cdot (12 — (-12)) \cdot 12 = 24 \cdot 6 = 144 \);
Ответ: 144.

а) \( \begin{cases} x \le 9 \\ y \le 0 \\ 2x + 5y \ge 10 \end{cases} \)

Рассмотрим каждое неравенство системы:

• \( x \le 9 \) — область на координатной плоскости, которая ограничена вертикальной прямой \( x = 9 \) и включает все точки слева от этой прямой.
• \( y \le 0 \) — область на координатной плоскости, которая ограничена горизонтальной прямой \( y = 0 \) и включает все точки ниже этой прямой.
• \( 2x + 5y \ge 10 \):
  • Преобразуем неравенство: \( 5y \ge -2x + 10 \).
  • Разделим обе части на \( 5 \): \( y \ge -\frac{2}{5}x + 2 \).
  • Это прямая \( y = -\frac{2}{5}x + 2 \), причем область решений находится выше этой прямой.

Теперь найдем точку пересечения прямой \( y = -\frac{2}{5}x + 2 \) с прямой \( x = 9 \):

• Подставим \( x = 9 \) в уравнение прямой:\( y(9) = -\frac{2}{5} \cdot 9 + 2 \).
• Выполним вычисления:\( y(9) = -\frac{18}{5} + 2 = -3,6 + 2 = -1,6 \).
• Таким образом, точка пересечения имеет координаты \( (9, -1,6) \).

Рассмотрим фигуру, заданную системой неравенств. Это треугольник с вершинами:

• \( (9, -1,6) \) — точка пересечения первой и третьей прямой.
• \( (5, 0) \) — точка пересечения прямой \( y = -\frac{2}{5}x + 2 \) с прямой \( y = 0 \):
  • Подставим \( y = 0 \) в уравнение \( y = -\frac{2}{5}x + 2 \):\( 0 = -\frac{2}{5}x + 2 \).
  • Решим уравнение:\( \frac{2}{5}x = 2 \), \( x = 5 \).
  • Таким образом, точка пересечения имеет координаты \( (5, 0) \).
• \( (9, 0) \) — точка пересечения прямой \( x = 9 \) с прямой \( y = 0 \).

Теперь найдем площадь треугольника:

• Формула площади треугольника:\( S = \frac{1}{2} \cdot основание \cdot высота \).
• Основание треугольника — расстояние между точками \( (9, 0) \) и \( (5, 0) \):\( 9 — 5 = 4 \).
• Высота треугольника — расстояние от точки \( (9, -1,6) \) до прямой \( y = 0 \):\( | -1,6 | = 1,6 \).
• Подставим значения в формулу:\( S = \frac{1}{2} \cdot 4 \cdot 1,6 = 0,8 \cdot 4 = 3,2 \).

Ответ: \( 3,2 \).

б) \( \begin{cases} x + y \le 12 \\ y — x \le 12 \\ y \ge 0 \end{cases} \)

Рассмотрим каждое неравенство системы:

• \( x + y \le 12 \):
  • Преобразуем неравенство: \( y \le 12 — x \).
  • Это прямая \( y = 12 — x \), причем область решений находится ниже этой прямой.
• \( y — x \le 12 \):
  • Преобразуем неравенство: \( y \le x + 12 \).
  • Это прямая \( y = x + 12 \), причем область решений находится ниже этой прямой.
• \( y \ge 0 \) — область на координатной плоскости, которая ограничена прямой \( y = 0 \) и включает все точки выше этой прямой.

Рассмотрим фигуру, заданную системой неравенств. Это треугольник с вершинами:

• \( (12, 0) \) — точка пересечения прямой \( y = 12 — x \) с прямой \( y = 0 \):
  • Подставим \( y = 0 \) в уравнение \( y = 12 — x \):\( 0 = 12 — x \), \( x = 12 \).
  • Таким образом, точка пересечения имеет координаты \( (12, 0) \).
• \( (-12, 0) \) — точка пересечения прямой \( y = x + 12 \) с прямой \( y = 0 \):
  • Подставим \( y = 0 \) в уравнение \( y = x + 12 \):\( 0 = x + 12 \), \( x = -12 \).
  • Таким образом, точка пересечения имеет координаты \( (-12, 0) \).
• \( (0, 12) \) — точка пересечения прямых \( y = 12 — x \) и \( y = x + 12 \):
  • Приравняем \( 12 — x = x + 12 \):\( 12 — x = x + 12 \), \( 12 = 2x + 12 \), \( 0 = 2x \), \( x = 0 \).
  • Подставим \( x = 0 \) в любое из уравнений:\( y = 12 — 0 = 12 \).
  • Таким образом, точка пересечения имеет координаты \( (0, 12) \).

Теперь найдем площадь треугольника:

• Формула площади треугольника:\( S = \frac{1}{2} \cdot основание \cdot высота \).
• Основание треугольника — расстояние между точками \( (12, 0) \) и \( (-12, 0) \):\( 12 — (-12) = 24 \).
• Высота треугольника — расстояние от точки \( (0, 12) \) до прямой \( y = 0 \):\( | 12 | = 12 \).
• Подставим значения в формулу:\( S = \frac{1}{2} \cdot 24 \cdot 12 = 12 \cdot 12 = 144 \).

Ответ: \( 144 \).