Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.24 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Случайным образом выбирают одно из решений системы неравенств
\(
\begin{cases}
|x — y| \le 2 \\
|x + y| \le 2
\end{cases}\)
Найдите вероятность того, что выбранная точка расположена:
а) ниже прямой у = 1;
б) выше прямой у = 0,5;
в) правее прямой х = 1;
г) выше параболы у = х².
Случайным образом выбирают одно из решений системы неравенств:
\(
\begin{cases}
|x — y| \le 2 \\
|x + y| \le 2
\end{cases}
\Rightarrow
\begin{cases}
-2 \le x — y \le 2 \\
-2 \le x + y \le 2
\end{cases}
\Rightarrow
\begin{cases}
y \le x + 2 \\
y \ge x — 2 \\
y \ge -x — 2 \\
y \le 2 — x
\end{cases};
\)
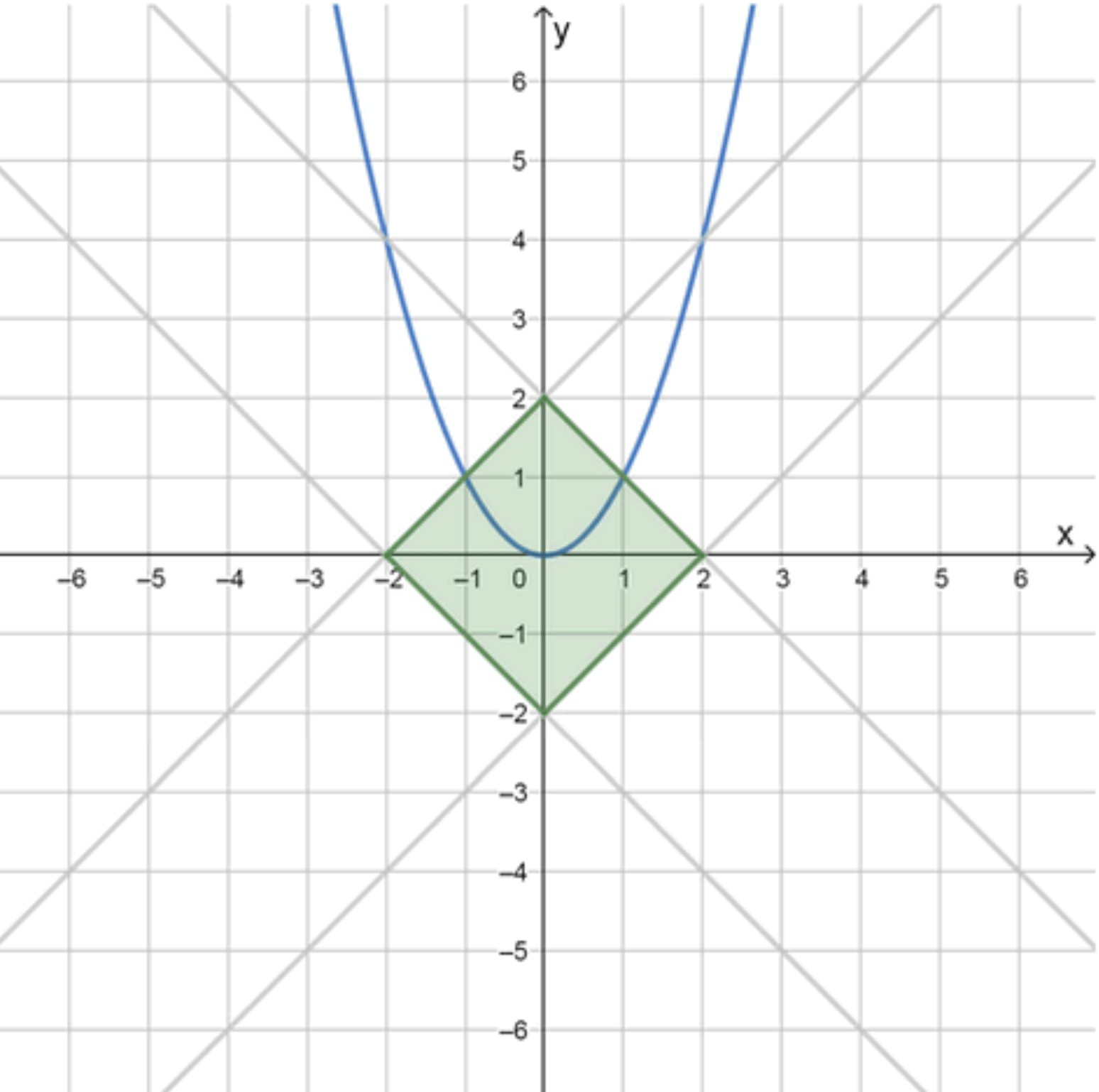
Множество решений:
Площадь данной фигуры:
\(
S = 2 \cdot \frac{1}{2} \cdot (2 — (-2)) \cdot 2 = 4 \cdot 2 = 8;
\)
а) Вероятность, что выбранная точка лежит ниже прямой \( y = 1 \):
\(
P = \frac{S — S_1}{S} = \frac{8 — \frac{1}{2} \cdot (1 — (-1)) \cdot 1}{8} = \frac{8 — \frac{1}{2} \cdot 2}{8} = \frac{8 — 1}{8} = \frac{7}{8};
\)
Ответ: \( \frac{7}{8} \)
б) Вероятность, что выбранная точка лежит выше прямой \( y = 0,5 \):
\(
P = \frac{S_1}{S} = \frac{\frac{1}{2} \cdot (1,5 — (-1,5)) \cdot 1,5}{8} = \frac{2 \cdot 3 \cdot 1,5}{8 \cdot 4} = \frac{3 \cdot 3}{32} = \frac{9}{32};
\)
Ответ: \( \frac{9}{32} \).
в) Вероятность, что выбранная точка лежит правее прямой \( x = 1 \):
\(
P = \frac{S_1}{S} = \frac{\frac{1}{2} \cdot (1 — (-1)) \cdot 1}{8} = \frac{\frac{1}{2} \cdot 2}{8} = \frac{1}{8};
\)
Ответ: \( \frac{1}{8} \).
г) Вероятность, что выбранная точка лежит выше параболы \( y = x^2 \):
\(
S_1 = \int_{-1}^{0} ((x + 2) — x^2) + \int_{0}^{1} ((2 — x) — x^2);
\)
\(
S_1 = \left( \frac{x^2}{2} + 2x — \frac{x^3}{3} \right) \Bigg|_{-1}^{0} + \left( 2x — \frac{x^2}{2} — \frac{x^3}{3} \right) \Bigg|_{0}^{1};
\)
\(
S_1 = -\left( \frac{(-1)^2}{2} + 2 \cdot (-1) — \frac{(-1)^3}{3} \right) + \left( 2 \cdot 1 — \frac{1^2}{2} — \frac{1^3}{3} \right);
\)
\(
S_1 = 2 — \frac{1}{2} — \frac{1}{3} — \frac{1}{2} + 2 — \frac{1}{3} = 4 — 1 — \frac{2}{3} = 3 — \frac{2}{3} = \frac{7}{3};
\)
\(
P = \frac{S_1}{S} = \frac{7}{3} : 8 = \frac{7}{24};
\)
Ответ: \( \frac{7}{24} \).
Случайным образом выбирают одно из решений системы неравенств:
\(
\begin{cases}
|x — y| \leq 2 \\
|x + y| \leq 2
\end{cases}
\Rightarrow
\begin{cases}
-2 \leq x — y \leq 2 \\
-2 \leq x + y \leq 2
\end{cases}
\Rightarrow
\begin{cases}
y \leq x + 2 \\
y \geq x — 2 \\
y \geq -x — 2 \\
y \leq 2 — x
\end{cases};
\)
Множество решений:
Площадь данной фигуры:
\(S = 2 \cdot \frac{1}{2} \cdot ((2) — (-2)) \cdot (2) = (4) \cdot (2) = (8);\)
а) Вероятность, что выбранная точка лежит ниже прямой \( y = 1 \):
Вычислим площадь \( S_1 \), которая соответствует области выше прямой \( y = 1 \):
Прямая \( y = 1 \) делит фигуру на две части. Верхняя часть представляет собой треугольник с вершинами в точках пересечения прямой \( y = 1 \) с границами фигуры.
Эти точки пересечения находятся на прямых \( y = x + 2 \) и \( y = 2 — x \).
Решим уравнения пересечения:
\(y = x + 2, \quad y = 1 \quad \Rightarrow \quad 1 = x + 2 \quad \Rightarrow \quad x = -1;\)
\(y = 2 — x, \quad y = 1 \quad \Rightarrow \quad 1 = 2 — x \quad \Rightarrow \quad x = 1.\)
Таким образом, вершины треугольника: \( (-1, 1), (1, 1), (0, -1) \).
Площадь треугольника вычисляется по формуле:
\(S_1 = \frac{1}{2} \cdot ((1) — (-1)) \cdot (1) = \frac{1}{2} \cdot (2) \cdot (1) = (1).\)
Теперь вероятность:
\(P = \frac{S — S_1}{S} = \frac{(8) — (1)}{(8)} = \frac{(7)}{(8)}.\)
Ответ: \( \frac{7}{8} \)
б) Вероятность, что выбранная точка лежит выше прямой \( y = 0,5 \):
Вычислим площадь \( S_1 \), которая соответствует области ниже прямой \( y = 0,5 \):
Прямая \( y = 0,5 \) пересекает границы фигуры в точках:
\(y = x + 2, \quad y = 0,5 \quad \Rightarrow \quad 0,5 = x + 2 \quad \Rightarrow \quad x = -1,5;\)
\(y = 2 — x, \quad y = 0,5 \quad \Rightarrow \quad 0,5 = 2 — x \quad \Rightarrow \quad x = 1,5.\)
Таким образом, вершины треугольника: \( (-1,5, 0,5), (1,5, 0,5), (0, -1,5) \).
Площадь треугольника:
\(S_1 = \frac{1}{2} \cdot ((1,5) — (-1,5)) \cdot (1,5) = \frac{1}{2} \cdot (3) \cdot (1,5) = \frac{4,5}{2} = (2,25).\)
Теперь вероятность:
\(P = \frac{S_1}{S} = \frac{(2,25)}{(8)} = \frac{9}{32}.\)
Ответ: \( \frac{9}{32} \).
в) Вероятность, что выбранная точка лежит правее прямой \( x = 1 \):
Площадь области правее прямой \( x = 1 \) представляет собой треугольник с вершинами:
\( (1, -1), (1, 1), (2, 0) \).
Площадь треугольника:
\(S_1 = \frac{1}{2} \cdot ((1) — (-1)) \cdot (1) = \frac{1}{2} \cdot (2) \cdot (1) = (1).\)
Теперь вероятность:
\(P = \frac{S_1}{S} = \frac{(1)}{(8)} = \frac{1}{8}.\)
Ответ: \( \frac{1}{8} \).
г) Вероятность, что выбранная точка лежит выше параболы \( y = x^2 \):
Площадь области выше параболы \( y = x^2 \) вычисляется через интегралы:
Разобьем интеграл на две части:
\(S_1 = \int_{-1}^{0} ((x + 2) — x^2) dx + \int_{0}^{1} ((2 — x) — x^2) dx.\)
Вычислим первый интеграл:
\(\int_{-1}^{0} ((x + 2) — x^2) dx = \int_{-1}^{0} (x + 2) dx — \int_{-1}^{0} x^2 dx.\)
Для каждого компонента:
\(\int_{-1}^{0} (x + 2) dx = \left( \frac{x^2}{2} + 2x \right) \Big|_{-1}^{0} = \left( \frac{0^2}{2} + 2 \cdot 0 \right) — \left( \frac{(-1)^2}{2} + 2 \cdot (-1) \right) =\)
\(= 0 — \left( \frac{1}{2} — 2 \right) = \frac{3}{2}.\)
\(\int_{-1}^{0} x^2 dx = \left( \frac{x^3}{3} \right) \Big|_{-1}^{0} = \frac{0^3}{3} — \frac{(-1)^3}{3} = 0 — \left( -\frac{1}{3} \right) = \frac{1}{3}.\)
Таким образом:
\(\int_{-1}^{0} ((x + 2) — x^2) dx = \frac{3}{2} — \frac{1}{3} = \frac{9}{6} — \frac{2}{6} = \frac{7}{6}.\)
Аналогично для второго интеграла:
\(\int_{0}^{1} ((2 — x) — x^2) dx = \int_{0}^{1} (2 — x) dx — \int_{0}^{1} x^2 dx.\)
Для каждого компонента:
\(\int_{0}^{1} (2 — x) dx = \left( 2x — \frac{x^2}{2} \right) \Big|_{0}^{1} = \left( 2 \cdot 1 — \frac{1^2}{2} \right) — \left( 2 \cdot 0 — \frac{0^2}{2} \right) = 2 — \frac{1}{2} =\)
\(= \frac{3}{2}.\)
\(\int_{0}^{1} x^2 dx = \left( \frac{x^3}{3} \right) \Big|_{0}^{1} = \frac{1^3}{3} — \frac{0^3}{3} = \frac{1}{3}.\)
Таким образом:
\(\int_{0}^{1} ((2 — x) — x^2) dx = \frac{3}{2} — \frac{1}{3} = \frac{9}{6} — \frac{2}{6} = \frac{7}{6}.\)
Общая площадь:
\(S_1 = \frac{7}{6} + \frac{7}{6} = \frac{14}{6} = \frac{7}{3}.\)
Теперь вероятность:
\(P = \frac{S_1}{S} = \frac{\frac{7}{3}}{8} = \frac{7}{24}.\)
Ответ: \( \frac{7}{24} \).