Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 58.4 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
а) \(x^2 — y^2 = 0\)
б) \(x^2 + 7xy — 18y^2 = 0\)
в) \(x^2 + 2xy + y^2 = 0\)
г) \(x^2 — 3xy + 2y^2 = 0\)
Построить график уравнения:
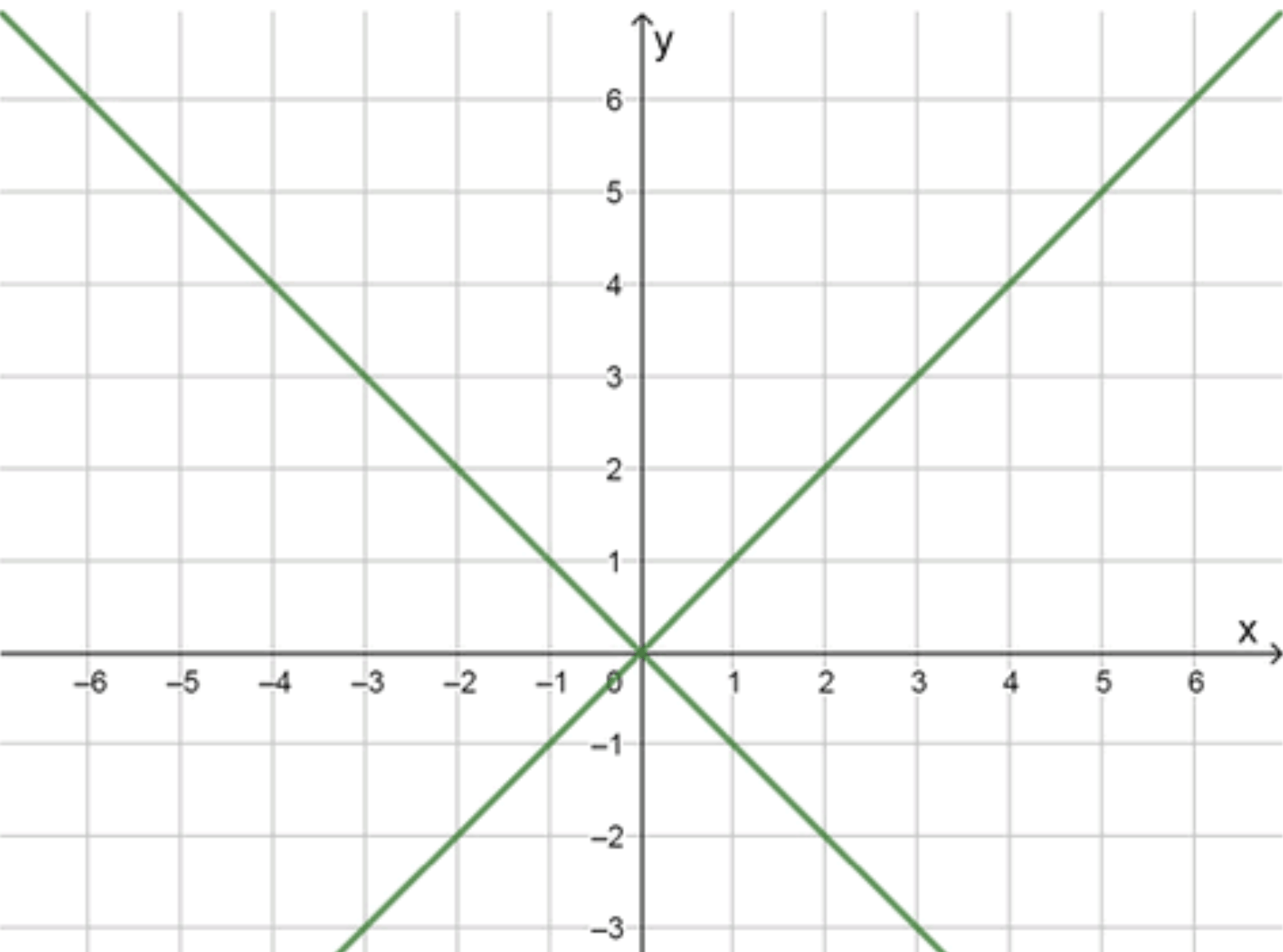
а) \(x^2 — y^2 = 0\)
\((x + y)(x — y) = 0\).
Первое уравнение:
\(x + y = 0\),
\(y = -x\).
Второе уравнение:
\(x — y = 0\),
\(y = x\).
График уравнения:
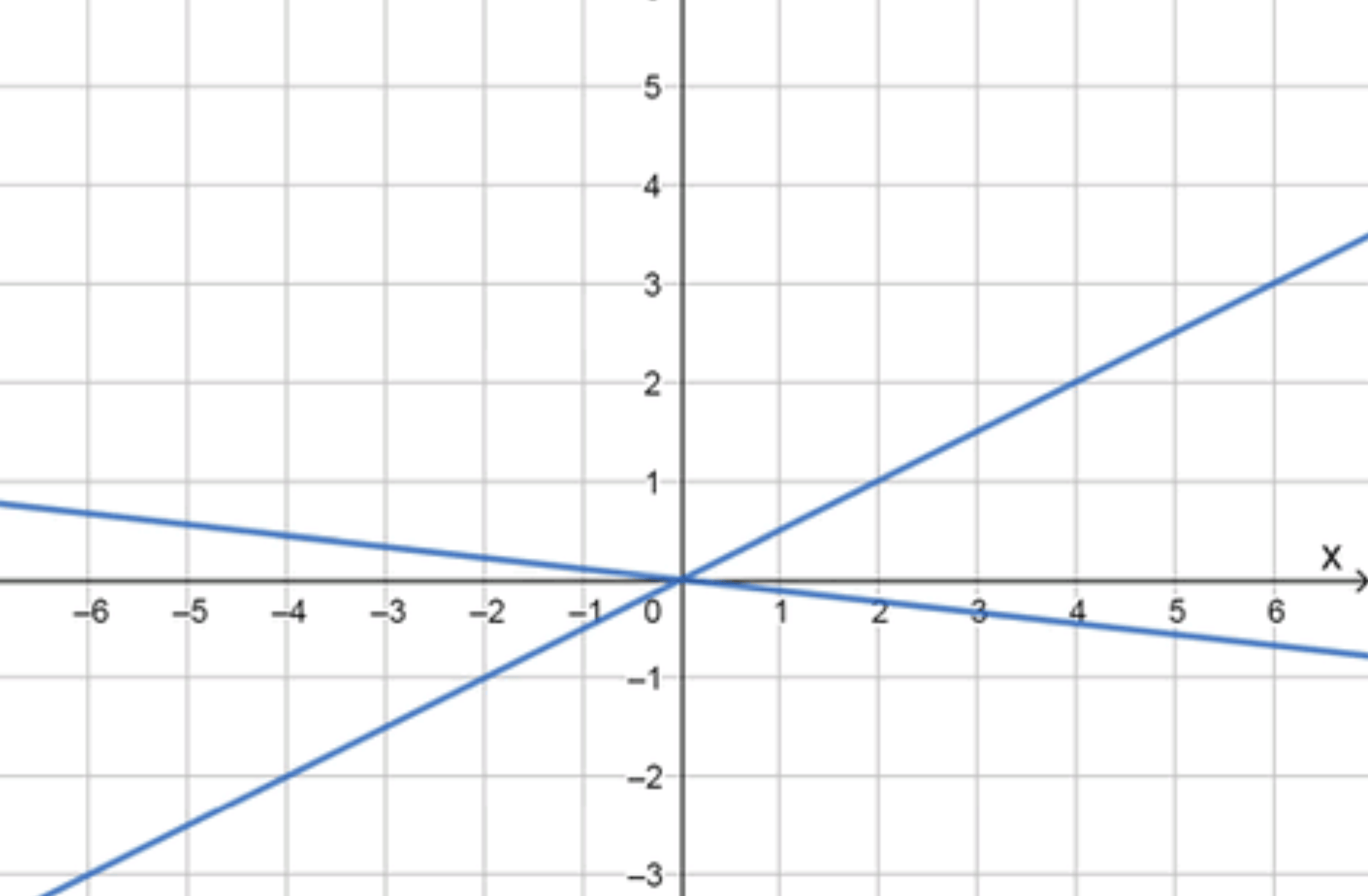
б) \(x^2 + 7xy — 18y^2 = 0\)
\(x^2 — 2xy + 9xy — 18y^2 = 0\).
\(x(x — 2y) + 9y(x — 2y) = 0\).
\((x + 9y)(x — 2y) = 0\).
Первое уравнение:
\(x + 9y = 0\),
\(9y = -x\),
\(y = -\frac{1}{9}x\).
Второе уравнение:
\(x — 2y = 0\),
\(2y = x\),
\(y = \frac{1}{2}x\).
График уравнения:
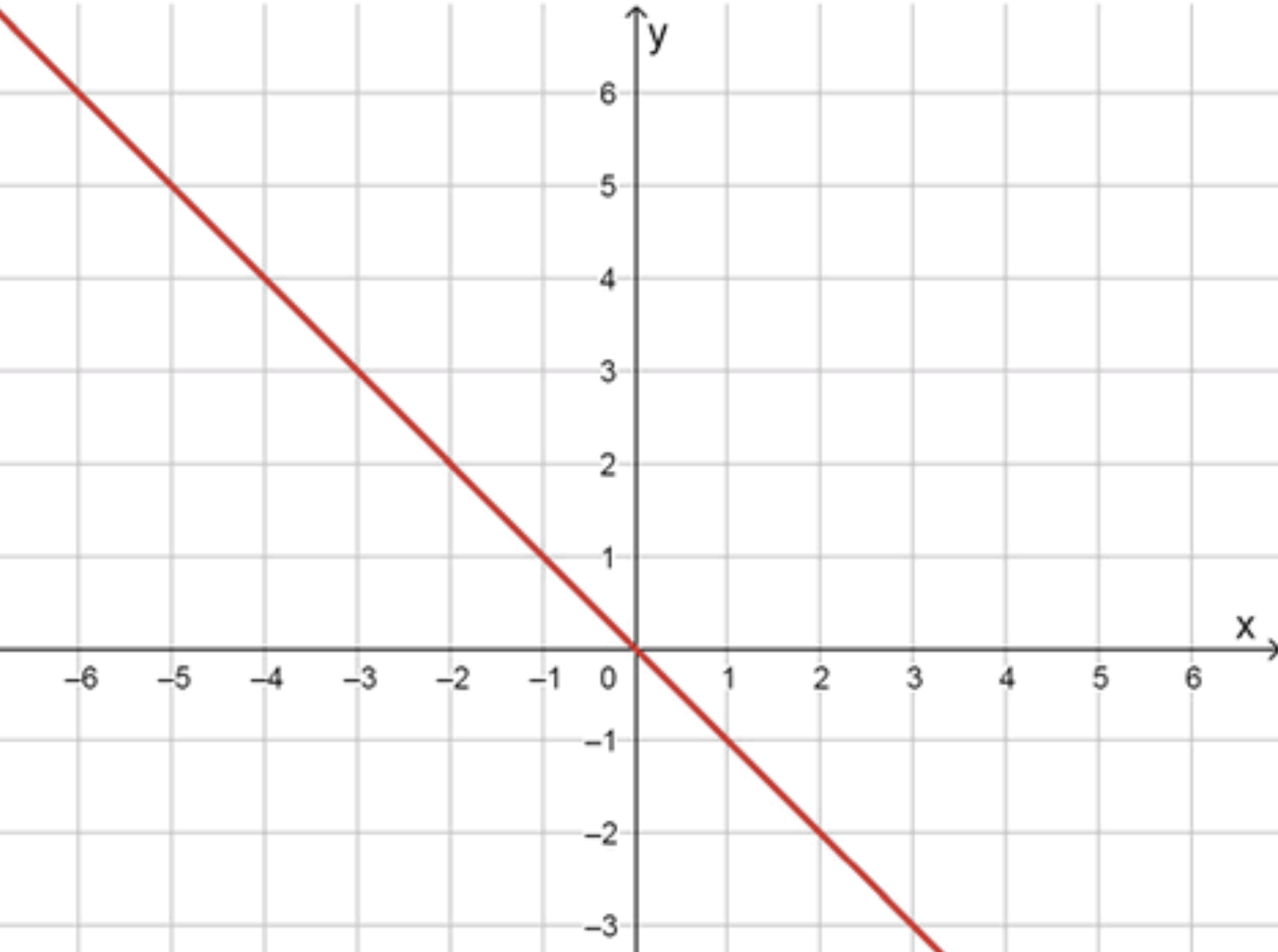
в) \(x^2 + 2xy + y^2 = 0\)
\((x + y)^2 = 0\).
\(x + y = 0\),
\(y = -x\).
График уравнения:
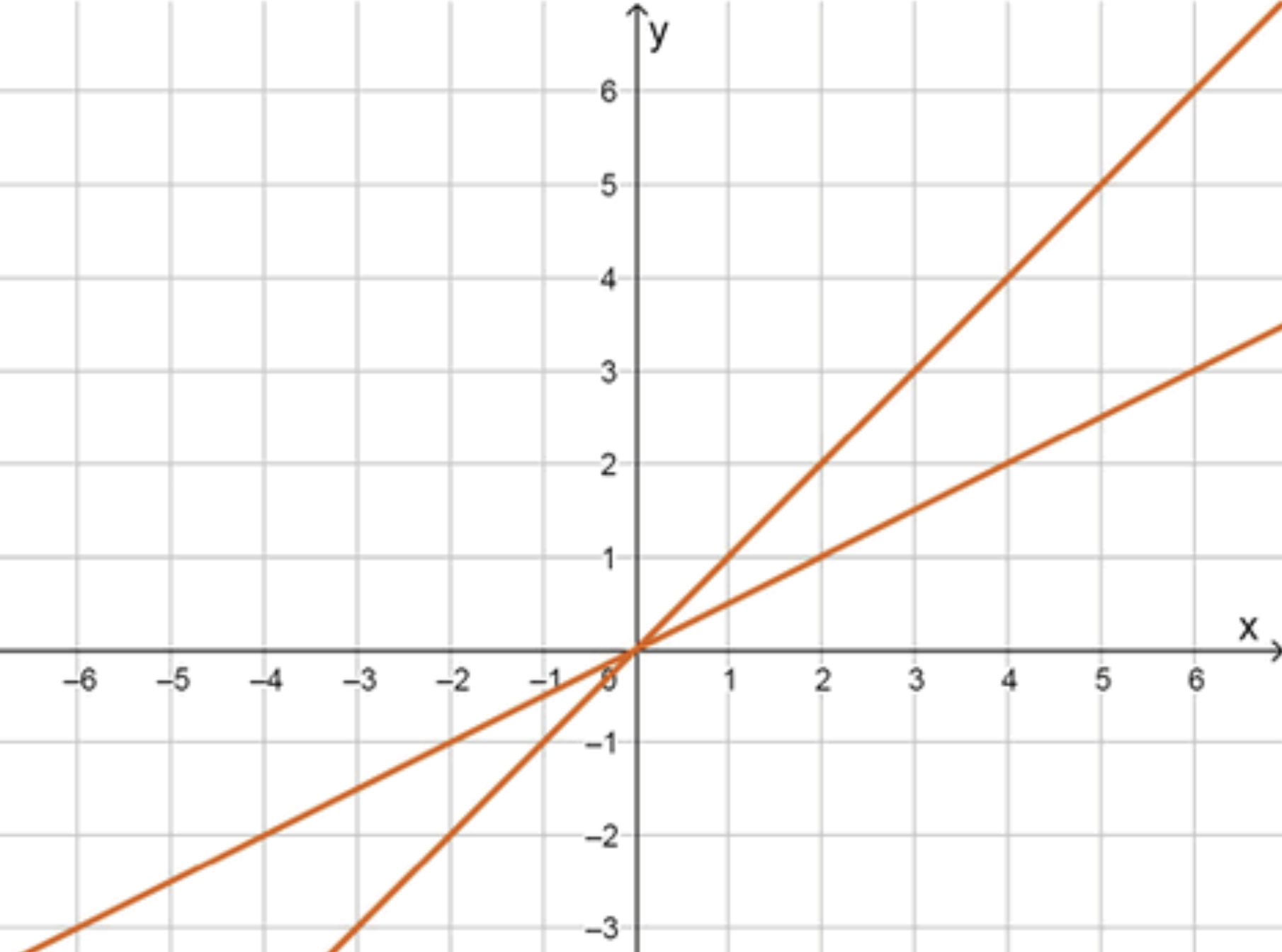
г) \(x^2 — 3xy + 2y^2 = 0\)
\(x^2 — xy — 2xy + 2y^2 = 0\).
\(x(x — y) — 2y(x — y) = 0\).
\((x — 2y)(x — y) = 0\).
Первое уравнение:
\(x — 2y = 0\),
\(2y = x\),
\(y = \frac{1}{2}x\).
Второе уравнение:
\(x — y = 0\),
\(y = x\).
График уравнения:
а) \(x^2 — y^2 = 0\)
Исходное уравнение:
\(x^2 — y^2 = 0\).
Воспользуемся формулой разности квадратов:
\((x + y)(x — y) = 0\).
Произведение равно нулю, если хотя бы один из множителей равен нулю:
- Первый множитель: \(x + y = 0\).
- Второй множитель: \(x — y = 0\).
Рассмотрим первый множитель:
\(x + y = 0\).
Выразим \(y\):
\(y = -x\).
Это уравнение задаёт прямую, проходящую через начало координат с угловым коэффициентом \(-1\).
Рассмотрим второй множитель:
\(x — y = 0\).
Выразим \(y\):
\(y = x\).
Это уравнение задаёт прямую, проходящую через начало координат с угловым коэффициентом \(1\).
График состоит из двух пересекающихся прямых:
- Прямая \(y = -x\).
- Прямая \(y = x\).
б) \(x^2 + 7xy — 18y^2 = 0\)
Исходное уравнение:
\(x^2 + 7xy — 18y^2 = 0\).
Разобьём средний член \(7xy\) на два слагаемых:
\(x^2 — 2xy + 9xy — 18y^2 = 0\).
Сгруппируем слагаемые:
\(x(x — 2y) + 9y(x — 2y) = 0\).
Вынесем общий множитель \((x — 2y)\):
\((x + 9y)(x — 2y) = 0\).
Произведение равно нулю, если хотя бы один из множителей равен нулю:
- Первый множитель: \(x + 9y = 0\).
- Второй множитель: \(x — 2y = 0\).
Рассмотрим первый множитель:
\(x + 9y = 0\).
Выразим \(y\):
\(9y = -x\),
\(y = -\frac{1}{9}x\).
Это уравнение задаёт прямую, проходящую через начало координат с угловым коэффициентом \(-\frac{1}{9}\).
Рассмотрим второй множитель:
\(x — 2y = 0\).
Выразим \(y\):
\(2y = x\),
\(y = \frac{1}{2}x\).
Это уравнение задаёт прямую, проходящую через начало координат с угловым коэффициентом \(\frac{1}{2}\).
График состоит из двух пересекающихся прямых:
- Прямая \(y = -\frac{1}{9}x\).
- Прямая \(y = \frac{1}{2}x\).
в) \(x^2 + 2xy + y^2 = 0\)
Исходное уравнение:
\(x^2 + 2xy + y^2 = 0\).
Заметим, что это полный квадрат суммы:
\((x + y)^2 = 0\).
Квадрат равен нулю, если его основание равно нулю:
\(x + y = 0\).
Выразим \(y\):
\(y = -x\).
Это уравнение задаёт прямую, проходящую через начало координат с угловым коэффициентом \(-1\).
График состоит из одной прямой:
- Прямая \(y = -x\).
г) \(x^2 — 3xy + 2y^2 = 0\)
Исходное уравнение:
\(x^2 — 3xy + 2y^2 = 0\).
Разобьём средний член \(-3xy\) на два слагаемых:
\(x^2 — xy — 2xy + 2y^2 = 0\).
Сгруппируем слагаемые:
\(x(x — y) — 2y(x — y) = 0\).
Вынесем общий множитель \((x — y)\):
\((x — 2y)(x — y) = 0\).
Произведение равно нулю, если хотя бы один из множителей равен нулю:
- Первый множитель: \(x — 2y = 0\).
- Второй множитель: \(x — y = 0\).
Рассмотрим первый множитель:
\(x — 2y = 0\).
Выразим \(y\):
\(2y = x\),
\(y = \frac{1}{2}x\).
Это уравнение задаёт прямую, проходящую через начало координат с угловым коэффициентом \(\frac{1}{2}\).
Рассмотрим второй множитель:
\(x — y = 0\).
Выразим \(y\):
\(y = x\).
Это уравнение задаёт прямую, проходящую через начало координат с угловым коэффициентом \(1\).
График состоит из двух пересекающихся прямых:
- Прямая \(y = \frac{1}{2}x\).
- Прямая \(y = x\).