ГДЗ 10-11 Класс Номер 58.5 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) \( \frac{x}{y} = 1 \);

б) \( \frac{2x + 3y — 5}{x + y} = 0 \);

в) \( \frac{x — y}{x + y — 2} = 0 \);

г) \( \frac{2x^2 — 4x — 2xy + 3y — 5}{x — y} = 2x \)

Построить график уравнения:

а) \( \frac{x}{y} = 1 \);
\( y = x \);
Выражение имеет смысл при:
\( y \ne 0 \);
График уравнения:

б) \( \frac{2x + 3y — 5}{x + y} = 0 \);
\( 2x + 3y — 5 = 0 \);
\( 3y = -2x + 5 \);
\( y = -\frac{2}{3}x + \frac{5}{3} \);
Дано уравнение прямой:
\[
\begin{array}{c|c|c}
x & -2 & 1 \\ \hline
y & 3 & 1
\end{array}
\]
Выражение имеет смысл при:
\( x + y \ne 0 \);
\( y \ne -x \);
График уравнения:

в) \( \frac{x — y}{x + y — 2} = 0 \);
\( x — y = 0 \);
\( y = x \);
Выражение имеет смысл при:
\( x + y — 2 \ne 0 \);
\( y \ne 2 — x \);
График уравнения:

г) \( \frac{2x^2 — 4x — 2xy + 3y — 5}{x — y} = 2x \);
\( 2x^2 — 4x — 2xy + 3y — 5 = 2x(x — y) \);
\( 2x^2 — 4x — 2xy + 3y — 5 = 2x^2 — 2xy \);
\( 3y = 4x + 5 \);
\( y = \frac{4}{3}x + \frac{5}{3} \);
Дано уравнение прямой:
\[
\begin{array}{c|c|c}
x & -2 & 1 \\ \hline
y & -1 & 3
\end{array}
\]
Выражение имеет смысл при:
\( x — y \ne 0 \);
\( y \ne x \);
График уравнения:

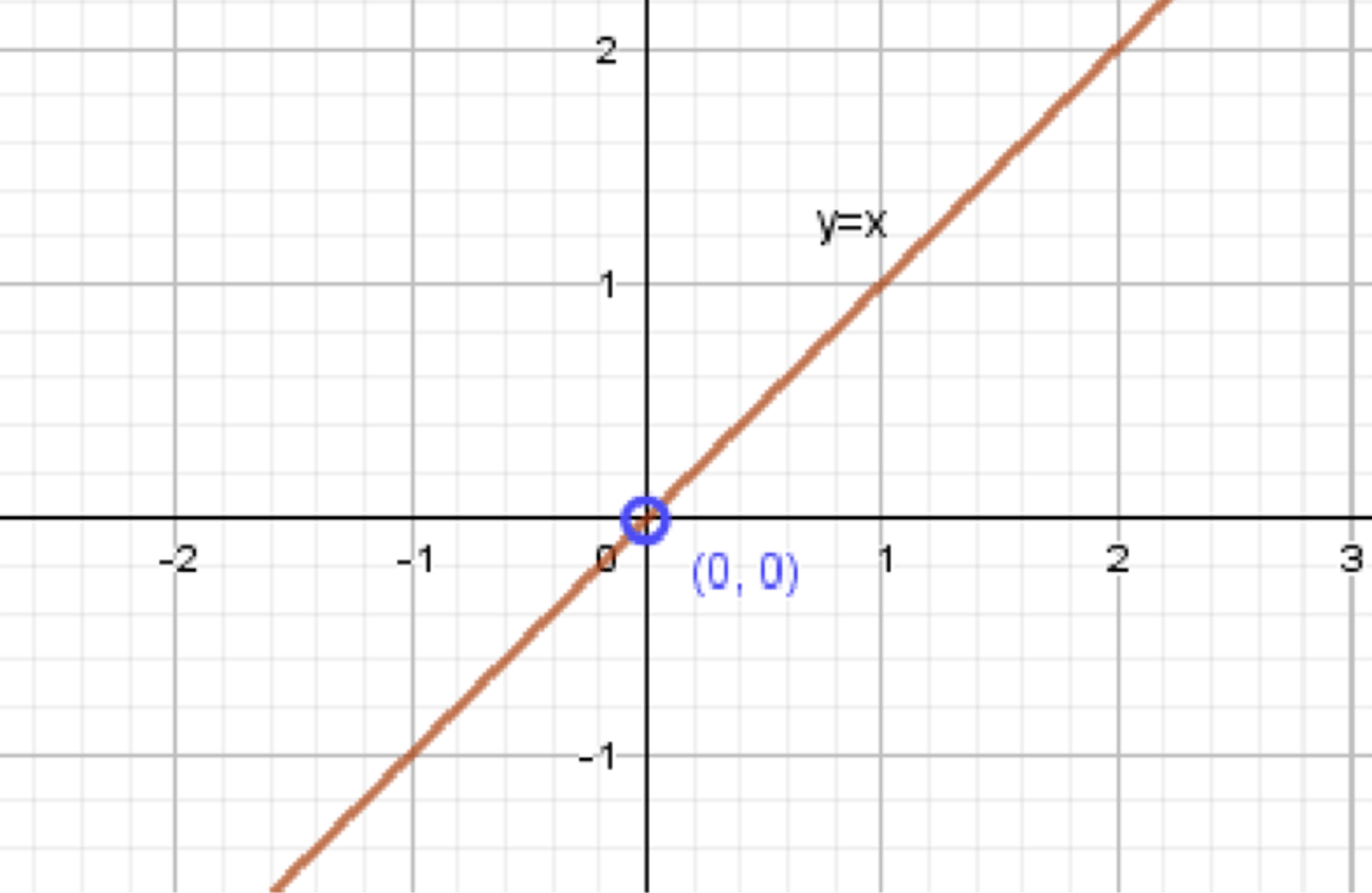
а) \( \frac{x}{y} = 1 \)

Уравнение \( \frac{x}{y} = 1 \) можно преобразовать, умножив обе части на \( y \) (при условии, что \( y \ne 0 \)):
\( x = y \).
Таким образом, уравнение принимает вид:
\( y = x \).

Выражение имеет смысл при условии:
\( y \ne 0 \).

График уравнения:
Прямая \( y = x \) проходит через начало координат и имеет угловой коэффициент, равный \( 1 \).
Это означает, что угол наклона прямой к положительному направлению оси \( x \) составляет \( 45^\circ \).
Точки на графике:
— При \( x = 1 \), \( y = 1 \);
— При \( x = -1 \), \( y = -1 \).

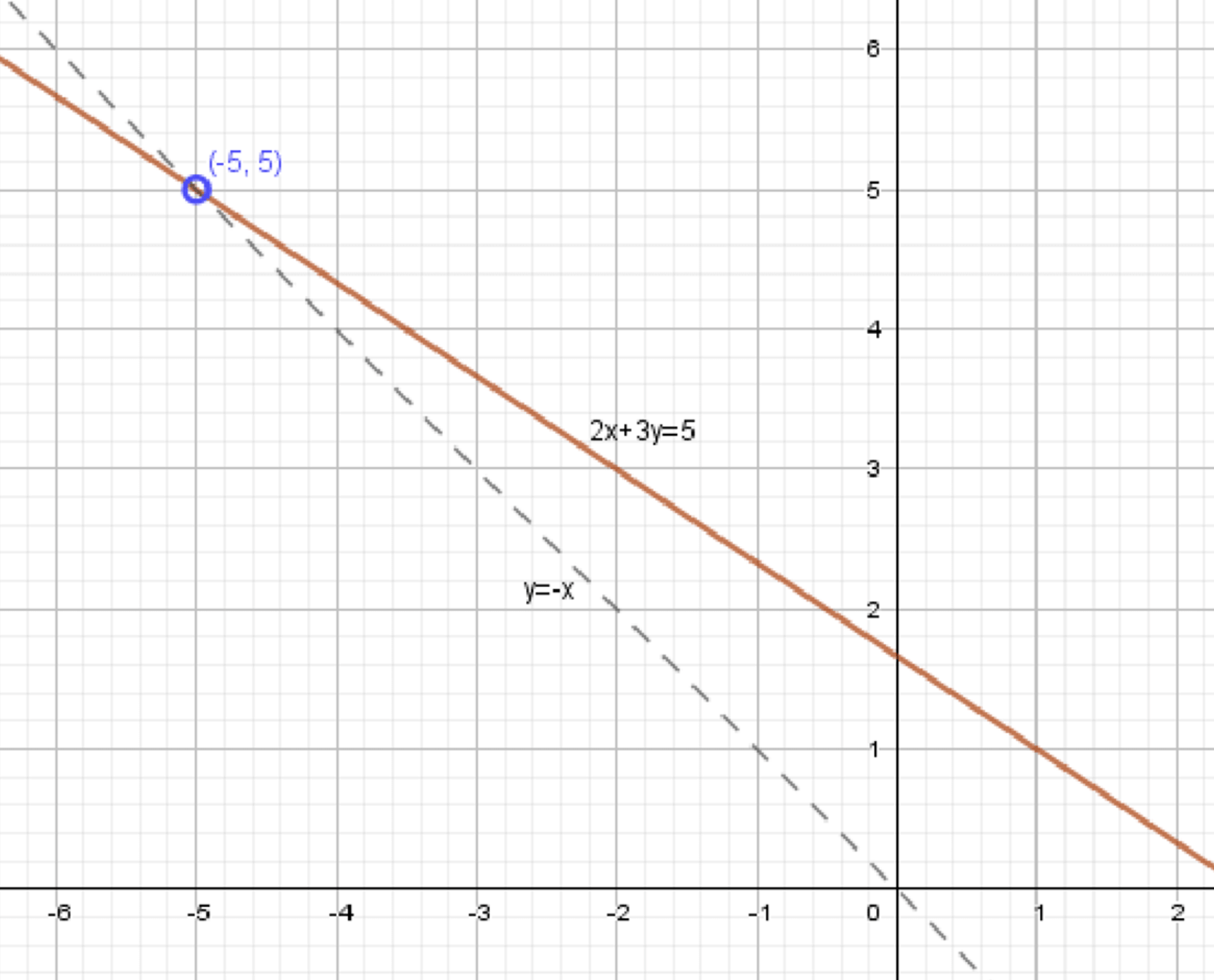
б) \( \frac{2x + 3y — 5}{x + y} = 0 \)

Уравнение \( \frac{2x + 3y — 5}{x + y} = 0 \) имеет смысл при \( x + y \ne 0 \), так как знаменатель не может быть равен нулю.
Условие: \( x + y \ne 0 \).
Числитель равен нулю:
\( 2x + 3y — 5 = 0 \).
Преобразуем уравнение:
\( 3y = -2x + 5 \).
Разделим обе части на \( 3 \):
\( y = -\frac{2}{3}x + \frac{5}{3} \).

Данное уравнение представляет собой прямую линию. Угловой коэффициент равен \( -\frac{2}{3} \), а точка пересечения с осью \( y \) — \( \frac{5}{3} \).
Точки на графике:
— При \( x = -2 \), \( y = 3 \);
— При \( x = 1 \), \( y = 1 \).

Выражение имеет смысл при условии:
\( x + y \ne 0 \);
\( y \ne -x \).

График уравнения:
Прямая \( y = -\frac{2}{3}x + \frac{5}{3} \) наклонена вниз.
Она пересекает ось \( y \) в точке \( (0, \frac{5}{3}) \) и ось \( x \) в точке \( (\frac{5}{2}, 0) \).

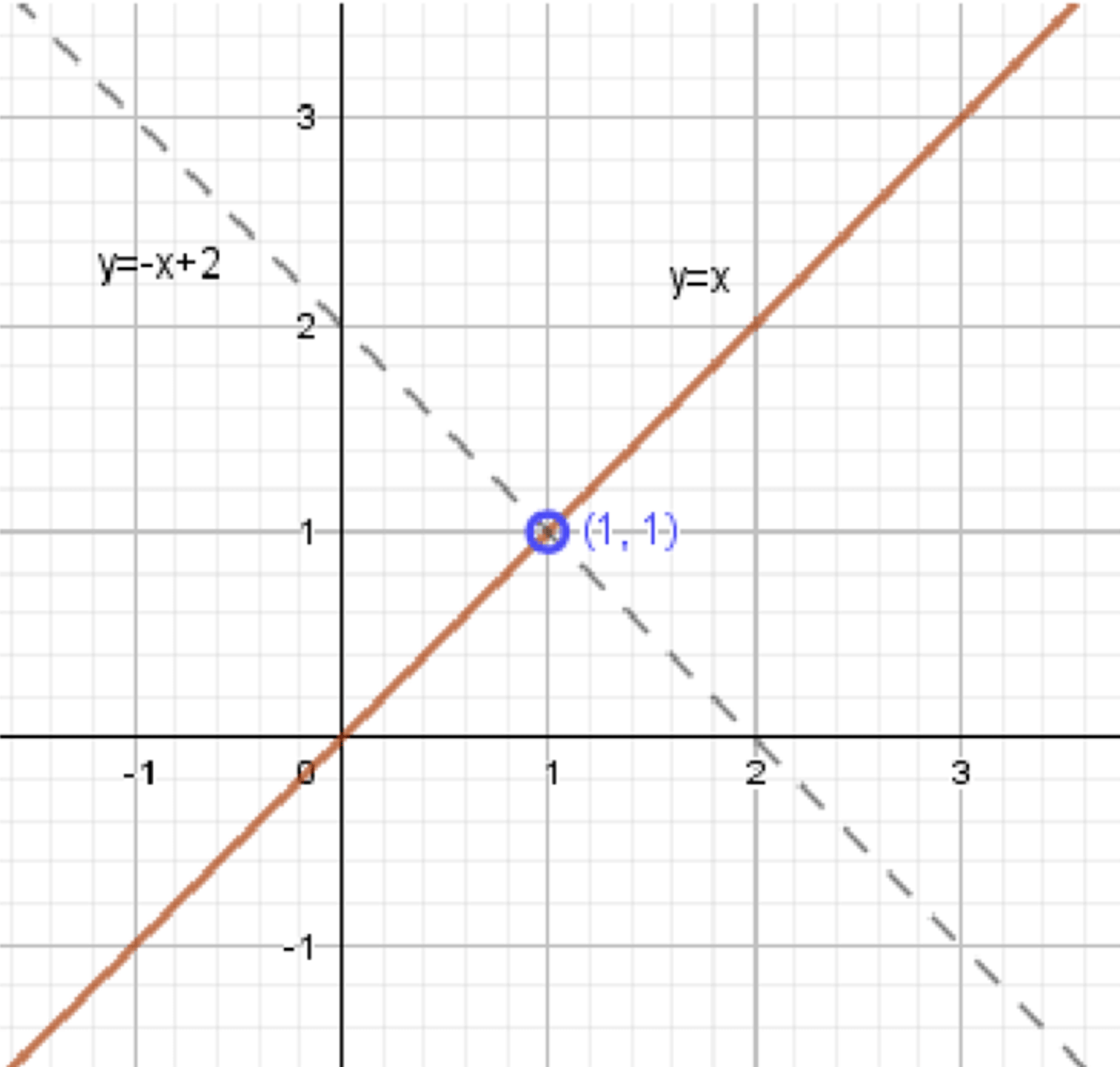
в) \( \frac{x — y}{x + y — 2} = 0 \)

Уравнение \( \frac{x — y}{x + y — 2} = 0 \) имеет смысл при \( x + y — 2 \ne 0 \), так как знаменатель не может быть равен нулю.
Условие: \( x + y — 2 \ne 0 \).
Числитель равен нулю:
\( x — y = 0 \).
Преобразуем уравнение:
\( y = x \).

Выражение имеет смысл при условии:
\( x + y — 2 \ne 0 \).
Преобразуем условие:
\( y \ne 2 — x \).

График уравнения:
Прямая \( y = x \) проходит через начало координат и имеет угловой коэффициент \( 1 \).
Точки на графике:
— При \( x = 1 \), \( y = 1 \);
— При \( x = -1 \), \( y = -1 \).

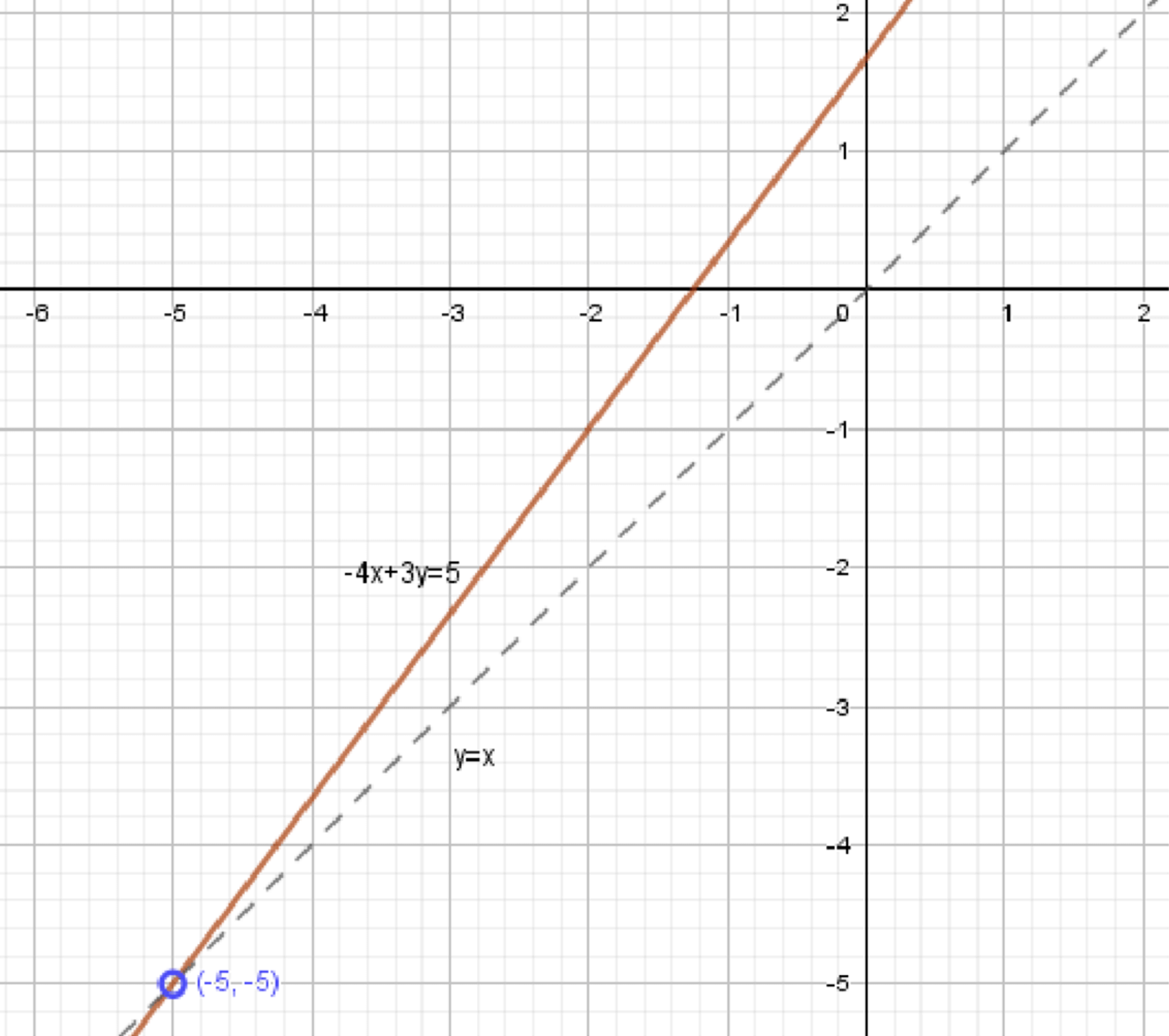
г) \( \frac{2x^2 — 4x — 2xy + 3y — 5}{x — y} = 2x \)

Уравнение \( \frac{2x^2 — 4x — 2xy + 3y — 5}{x — y} = 2x \) имеет смысл при \( x — y \ne 0 \), так как знаменатель не может быть равен нулю.
Условие: \( x — y \ne 0 \).
Умножим обе части уравнения на \( x — y \):
\( 2x^2 — 4x — 2xy + 3y — 5 = 2x(x — y) \).
Раскроем скобки:
\( 2x^2 — 4x — 2xy + 3y — 5 = 2x^2 — 2xy \).
Упростим:
\( 3y = 4x + 5 \).
Разделим обе части на \( 3 \):
\( y = \frac{4}{3}x + \frac{5}{3} \).

Данное уравнение представляет собой прямую линию. Угловой коэффициент равен \( \frac{4}{3} \), а точка пересечения с осью \( y \) — \( \frac{5}{3} \).
Точки на графике:
— При \( x = -2 \), \( y = -1 \);
— При \( x = 1 \), \( y = 3 \).

Выражение имеет смысл при условии:
\( x — y \ne 0 \);
\( y \ne x \).

График уравнения:
Прямая \( y = \frac{4}{3}x + \frac{5}{3} \) наклонена вверх.
Она пересекает ось \( y \) в точке \( (0, \frac{5}{3}) \) и ось \( x \) в точке \( (-\frac{5}{4}, 0) \).